23. Каноническое уравнение эллипса.

Теорема. В канонической для эллипса системе координат уравнение эллипса имеет вид:

                                   .                                     (4)

   Доказательство. Доказательство проведем в два этапа. На первом этапе мы докажем, что координаты любой точки, лежащей на эллипсе удовлетворяют уравнению (4). На втором этапе мы докажем, что любоерешение уравнения (4) дает координаты точки, лежащей на эллипсе. Отсюда будет следовать, что уравнению (4) удовлетворяют те и только те точки координатной плоскости, которые лежат на эллипсе. Отсюда и изопределения уравнения кривой будет следовать, что уравнение (4) является уравнением эллипса.

1) Пусть точка М(х, у) является точкой эллипса, т.е. сумма ее фокальных радиусов равна 2а:

                                   .

Воспользуемся формулой расстояния между двумя точками накоординатной плоскости и найдем по этой формуле фокальные радиусы данной точки М:

, , откуда получаем:

                 .

Перенесем один корень в правую часть равенства и возведем в квадрат:

.

Сокращая, получаем:

                     .

Приводим подобные, сокращаем на 4 и уединяем радикал:

                      .

Возводим в квадрат

               .

Раскрываем скобки и сокращаем на :

                  ,

откуда получаем:

                .

Используя равенство (2), получаем:

                                .

Разделив последнее равенство на , получаем равенство (4), ч.т.д.

2) Пусть теперь пара чисел (х, у) удовлетворяет уравнению (4) и пусть М(х, у) – соответствующая точка на координатной плоскости Оху.

   Тогда из (4) следует:

                               .

Подставляем это равенство в выражение для фокальных радиусов точки М:

.

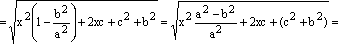
Здесь мы воспользовались равенством (2) и (3).

Таким образом, . Аналогично, .

Теперь заметим, что из равенства (4) следует, что

 или  и т.к. , то отсюда следует неравенство:

                              .

Отсюда, в свою очередь, следует, что

 или  и

                               , .                          (5)

Из равенств (5) следует, что , т.е. точка М(х, у) является точкой эллипса, ч.т.д.

Теорема доказана.

24. Каноническое уравнение гиперболы.

Теорема. В канонической для гиперболы системе координат уравнение гиперболы имеет вид:

                                   .                                     (4)

  

Доказательство. Доказательство проведем в два этапа. На первом этапе мы

докажем, что координаты любой точки, лежащей на гиперболе, удовлетворяют

уравнению (4). На втором этапе мы докажем, что любое решение уравнения

(4) дает координаты точки, лежащей на гиперболе. Отсюда будет

следовать, что уравнению (4) удовлетворяют координаты тех и только тех

точек координатной плоскости, которые лежат на гиперболе. Отсюда и из

определения уравнения кривой будет следовать, что уравнение (4)

является уравнением гиперболы.

1) Пусть точка М(х, у) является точкой гиперболы, т.е. модуль разности ее фокальных радиусов равен 2а:

                    или 

Воспользуемся

формулой расстояния между двумя точками на координатной плоскости и

найдем по этой формуле фокальные радиусы данной точки М:

, , откуда получаем:

                 .

Перенесем один корень в правую часть равенства и возведем в квадрат:

.

Сокращая, получаем:

                     .

Приводим подобные, сокращаем на 4 и уединяем радикал:

                      .

Возводим в квадрат

               .

Раскрываем скобки и сокращаем на :

                  ,

откуда получаем:

                .

Используя равенство (2), получаем:

                                .

Разделив последнее равенство на , получаем равенство (4), ч.т.д.

2)

Пусть теперь пара чисел (х, у) удовлетворяет уравнению (4) и пусть М(х,

у) – соответствующая точка на координатной плоскости Оху.

   Тогда из (4) следует:

                               .

Подставляем это равенство в выражение для фокального радиуса точки М:

.

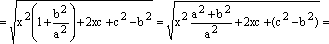
Здесь мы воспользовались равенством (2) и (3).

   Таким образом,

                                .

 Аналогично,

                                .

   Теперь заметим, что из равенства (4) следует, что

 или . Умножим неравенство

                                        

на :

                                 ,

                          .

Получаем:                             

               или .

Отсюда следует, что числа х,  и  имеют одинаковые знаки, т.е. при  и ,

а при  и , а значит

 и .

, т.е. , что означает принадлежность точки М(х, у) гиперболе, ч.т.д.

Теорема доказана.