6. Решение системы линейчатых неоднородных алгебраических уравнений средствами матричного исчисления.
Систему (1) записываем в матричной форме:
где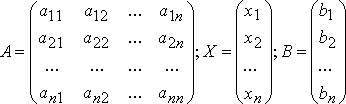 
.
Из
матричного уравнения следует, что 
где 
–
обратная матрица.
Обратная матрица имеет вид
,
где 
– алгебраическое
дополнение к элементу 
матрицы 
, 
– номер
строки, 
– номер
столбца, причем алгебраическое
дополнение 
–
это определитель, полученный из элементов
матрицы A путём
вычёркивания 
-й
строки и -го столбца.
7. Метод Гаусса решения систем линейных неоднородных алгебраических уравнений. Теорема Кронекера-Капелли.
Метод Гаусса прекрасно подходит для решения систем линейных алгебраических уравнений (СЛАУ). Он обладает рядом преимуществ по сравнению с другими методами:
во-первых, нет необходимости предварительно исследовать систему уравнений на совместность;
во-вторых, методом Гаусса можно решать не только СЛАУ, в которых число уравнений совпадает с количеством неизвестных переменных и основная матрица системы невырожденная, но и системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равен нулю;
в-третьих, метод Гаусса приводит к результату при сравнительно небольшом количестве вычислительных операций.
Рассмотрим
систему линейных уравнений 
Метод
Гаусса решения систем линейных уравнений
состоит из двух этапов, называемых
прямым и обратным ходом. Прямой ход
метода Гаусса заключается в том, что с
помощью элементарных преобразований
над расширенной матрицей система 
приводится
к «ступенчатому» виду.
Обратный ход метода Гаусса состоит в том, что, начиная с последнего уравнения ступенчатой системы, вычисляются неизвестные.
При реализации прямого хода метода Гаусса возможны следующие три случая.
1. В результате
преобразований в системе уравнений
будет получено уравнение вида 
где 
Ясно,
что никакой набор действительных чисел
этому уравнению удовлетворять не может,
поэтому в таком случае система уравнений
несовместна.
2. В результате преобразований получится ступенчатая система уравнений
в которой количество уравнений совпадает с количеством неизвестных.
В этом случае система уравнений является определённой.
В результате
преобразований получится система
уравнений ступенчатого вида, в которой
количество неизвестных больше числа
уравнений системы (
)
В этом случае
те неизвестные, которые стоят на
«ступеньках», называются главными
неизвестными (
),
а другие неизвестные называются
свободными (
);
система уравнений будет неопределённой.
Тогда обратный ход метода Гаусса состоит
в том, что начиная с последнего уравнения
системы, главные неизвестные выражаются
через свободные и составляется общее
решение системы уравнений. Для того
чтобы получить какое-либо частное
решение системы, свободным неизвестным
придают конкретные числовые значения,
вычисляя тем самым главные неизвестные.
Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:
|
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных. |
Для того, чтобы линейная система являлась совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу ее основной матрицы.