9. Проекция вектора на ось. Направляющие косинусы вектора.

Проекцией вектора на ось называется вектор, который получается в результате перемножения скалярной проекции вектора на эту ось и единичного вектора этой оси. Например, если а_x – скалярная проекция вектора а на ось X, то а_x·i - его векторная проекция на эту ось.  Обозначим  векторную проекцию также, как и сам вектор, но с индексом той оси на которую вектор проектируется. Так, векторную проекцию вектора а на ось Х обозначим  а_x (жирная буква, обозначающая вектор и нижний индекс названия оси) или (нежирная буква, обозначающая вектор, но со стрелкой наверху (!) и нижний индекс названия оси). 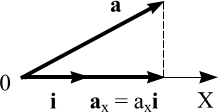Скалярной проекцией вектора на ось называется число, абсолютная величина которого равна длине отрезка оси (в выбранном масштабе), заключённого между проекциями точки начала и точки конца вектора. Обычно вместо выражения скалярная проекция говорят просто – проекция. Проекция обозначается той же буквой, что и проектируемый вектор (в обычном, нежирном написании), с нижним (как правило) индексом названия оси, на которую этот вектор проектируется. 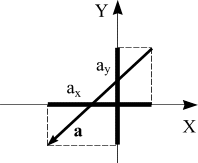Например, если на ось Х проектируется вектора, то его проекция обозначается а_x. При проектировании этого же вектора на другую ось, если  ось Y , его проекция будет обозначаться а_y . Чтобы вычислить проекцию вектора на ось (например, ось X) надо из координаты точки его конца вычесть координату точки начала, то есть а_x = х_к − x_н. Проекция вектора на ось - это число. Причем, проекция может быть положительной, если величина х_к больше величины х_н,  отрицательной,  если величина х_к меньше величины х_н  и равной нулю, если х_к равно х_н . 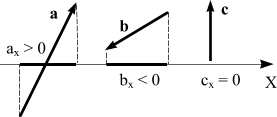Проекцию вектора на ось можно также найти, зная модуль вектора и угол, который он составляет с этой осью.  Из рисунка  видно, что а_x = а Cos α то есть, проекция вектора на ось равна произведению модуля вектора на косинус угла между направлением оси и направлением вектора. Если угол острый, то  Cos α > 0 и а_x > 0, а, если тупой, то косинус тупого угла отрицателен, и проекция вектора на ось тоже будет отрицательна. 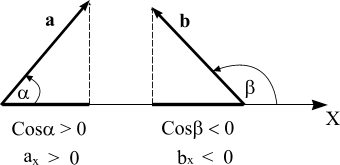Углы, отсчитываемые от оси против хода часовой стрелки, принято считать положительными, а по ходу - отрицательными. Однако, поскольку косинус – функция четная, то есть, Cos α = Cos (− α), то при вычислении проекций углы можно отсчитывать как по ходу часовой стрелки, так и против. Чтобы найти проекцию вектора на ось надо модуль этого вектора умножить на косинус угла между направлением оси и направлением вектора.

10. Линейные операции над векторами и их основные свойства. Линейные операции над векторами Сложение векторов

Пусть даны два вектора и . Приложим вектор к точке (концу вектора ) и получим вектор (рис.1.7,а; здесь и далее равные векторы отмечены одинаковыми засечками). Вектор называется суммой векторов и и обозначается . Это нахождение суммы называется правилом треугольника.

Сумму двух неколлинеарных векторов и можно найти по правилу параллелограмма. Для этого откладываем от любой точки векторы и , а затем строим параллелограмм (рис. 1.7,6). Диагональ параллелограмма определяет сумму:

Для нахождения суммы нескольких векторов можно построить ломаную из равных им векторов. Тогда замыкающий вектор, соединяющий начало первого вектора ломаной с концом последнего ее вектора, равен сумме всех векторов ломаной. На рис.1.7,в изображена сумма четырех векторов . Таким способом (правило ломаной) можно сложить любое конечное число векторов. Заметим, что сумма векторов не зависит от точек приложения слагаемых и от порядка суммирования. Например, "выстраивая цепочку" векторов для суммы в виде , получим вектор, равный вектору . Если ломаная получилась замкнутой, то сумма равна нулевому вектору.