35. Расстояние между перекрещивающимися прямыми в пространстве.
Пусть L1:x−x1m1=y−y1l1=z−z1k1 и L2:x−x2m2=y−y2l2=z−z2k2 - две скрещивающиеся прямые. Расстояние ρ(L1,L2) между прямыми L1 и L2 можно найти по следующей схеме:
1)
Находим уравнение плоскости P, проходящей
через прямую L1, параллельно
прямой L2: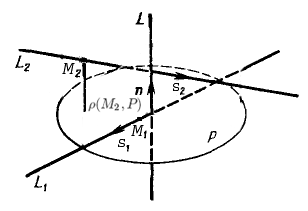
Плоскость P проходит через точку M1(x1,y1,z1), перпендикулярно вектору n¯¯=[s¯1,s¯2]=(nx,ny,nz), где s¯1=(m1,l1,k1) и s¯2=(m2,l2,k2) - направляющие вектора прямых L1 и L2.Следовательно, уравнение плоскости P:nx(x−x1)+ny(y−y1)+nz(z−z1)=0.
2) Расстояние между прямыми L1 и L2 равно расстоянию от любой точки прямой L2 до плоскости P:
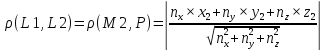
Нахождение общего перпендикуляра скрещивающихся прямых.
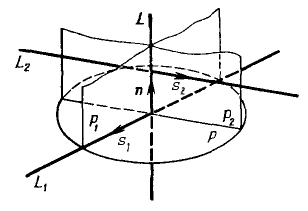
Для нахождения общего перпендикуляра прямых L1 и L2, необходимо найти уравнения плоскостей P1 и P2, проходящих, соответственно, через прямые L1 и L2, перпендикулярно плоскости P.
Пусть P1:A1x+B1y+C1z+D1=0;
P2:A2x+B2y+C2z+D2=0.
Тогда уравнение общего перпендикуляра имеет вид
{A1x+B1y+C1z+D1=0;A2x+B2y+C2z+D2=0.
36. Поверхности второго порядка. Эллипсоиды и гиперболоиды.
Поверхность второго порядка — геометрическое место точек трёхмерного пространства, прямоугольные координаты которых удовлетворяют уравнению вида
в
котором по крайней мере один из
коэффициентов 
, 
, 
, 
, 
, 
отличен
от нуля.
Поверхность,
задаваемая в некоторой прямоугольной
декартовой системе координат
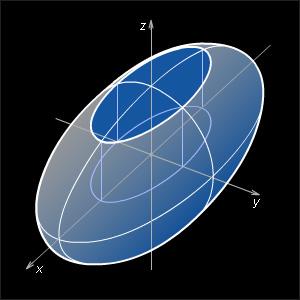
уравнение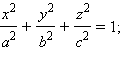м 
a > 0, b > 0, c > 0,
называется эллипсоидом.
|
|
|
Рисунок 5.7.1 |
Свойства эллипсоида.
Эллипсоид – ограниченная поверхность, поскольку из его уравнения следует, что
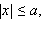
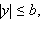
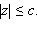
Эллипсоид обладает
центральной симметрией относительно начала координат,
осевой симметрией относительно координатных осей,
плоскостной симметрией относительно начала координат.
В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается эллипс.
|
|
|
Рисунок 5.7.2 |
Поверхность,
задаваемая в некоторой прямоугольной
декартовой системе координат
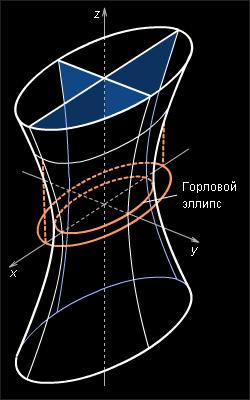
уравнение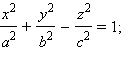м 
a > 0, b > 0, c > 0,
называется однополостным
гиперболоидом.
|
|
|
Рисунок 5.7.4 |
Свойства однополостного гиперболоида.
Однополостной гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.
Однополостной гиперболоид обладает
центральной симметрией относительно начала координат,
осевой симметрией относительно всех координатных осей,
плоскостной симметрией относительно всех координатных плоскостей.
В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz, получается эллипс, а плоскостями, ортогональными осям Ox и Oy – гипербола.
Определение 5.16. 
Поверхность,
задаваемая в некоторой прямоугольной
декартовой системе координат
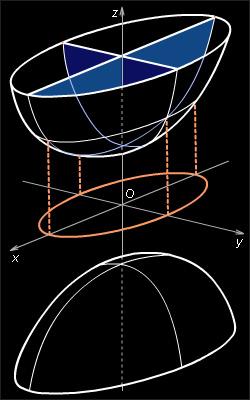
уравнение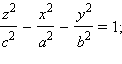м 
a > 0, b > 0, c > 0,
называетсядвуполостным
гиперболоидом.
|
|
|
Рисунок 5.7.5 |
Свойства двуполостного гиперболоида.
Двуполостный гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что
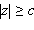и
неограничен сверху.Двуполостный гиперболоид обладает
центральной симметрией относительно начала координат,
осевой симметрией относительно всех координатных осей,
плоскостной симметрией относительно всех координатных плоскостей.
В
сечении однополостного гиперболоида
плоскостью, перпендикулярной оси
координат Oz,
при 
получается
эллипс, при
–
точка, а в сечении плоскостями,
перпендикулярными осямOx и Oy,
– гипербола.