28. Параметрическая форма задания уравнения линий в трехмерном пространстве.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz. Зададим в ней прямую a, указав направляющий вектор прямой и координаты некоторой точки прямой . От этих данных будем отталкиваться при составлении параметрических уравнений прямой в пространстве.

Пусть - произвольная точка трехмерного пространства. Если вычесть из координат точки М соответствующие координаты точки М₁, то мы получим координаты вектора , то есть, .

Очевидно, что множество точек определяет прямую а тогда и только тогда, когда векторы и коллинеарны.

Запишем необходимое и достаточное условие коллинеарности векторов и : , где - некоторое действительное число. Полученное уравнение называется векторно-параметрическим уравнением прямой в прямоугольной системе координат Oxyz в трехмерном пространстве. Векторно-параметрическое уравнение прямой в координатной форме имеет вид 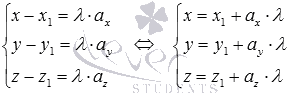и представляет собой параметрические уравнения прямой a. Название "параметрические" не случайно, так как координаты всех точек прямой задаются с помощью параметра .

Приведем пример параметрических уравнений прямой в прямоугольной системе координат Oxyz в пространстве: . Здесь .

29. Плоскость в трехмерном пространстве. Различные виды уравнений плоскости.

Изучение геометрических объектов с помощью метода координат начнем с простейших поверхностей и линий, а именно: плоскостей и прямых.

Определение. Линейным уравнением относительно переменных x, y, z называется уравнение вида Ax + By + Cz + D = 0, где хотя бы один из коэффициентов А, В, С отличен от нуля.

Теорема. Всякая плоскость в пространстве определяется линейным уравнением

и обратно, всякое линейное уравнение (3) определяет плоскость в пространстве.

Действительно, пусть в пространстве R³ задана плоскость (Р) (рис. 1).

Выбираем на ней какую-либо точку M₀(x_{0, y}0, z₀), и в некоторой точке плоскости (P)построим ненулевой вектор , перпендикулярный плоскости(P). Для того, чтобы произвольная точка M(x, y, z) пространства принадлежала плоскости (P), необходимо и достаточно, чтобы , то есть

Уравнение (4) называется векторным уравнением плоскости.

Т.к. и, то скалярное произведение в (4) можем заменить через координаты сомножителей, а именно:

Уравнение (5) перепишем в виде:

где D = -Ax₀ - By₀ - Cz₀, то есть получим уравнение (3). Это показывает, что любая плоскость может быть описана уравнением (3).

Уравнение (3) называют общим уравнением плоскости, а уравнение (5) - уравнением плоскости, проходящей через заданную точку M0(x0, y0, z0). <p< p="">class="maintext">Отметим, что вектор называют нормальным вектором плоскости и в качестве нормального вектора плоскости может быть взят любой ненулевой вектор, перпендикулярный плоскости.</p<>

Легко доказывается и обратное: дано уравнение Ax + By + Cz + D = 0 и нужно убедиться, что оно описывает плоскость в пространстве R³.

Пусть (x0, y0, z0) - какое-либо решение данного уравнения. Тогда Ax₀ + By₀ + Cz₀ + D = 0. Отсюда получаем D = -Ax₀ - By₀ - Cz₀ и, подставляя в исходное уравнение, получаем:  Ax + By + Cz -Ax₀ - By₀ - Cz₀ = 0, или  A(x - x₀) + B(y- y₀) + C(z - z₀) = 0. а это есть уравнение плоскости, проходящей через точку (x₀, y₀, z₀) и имеющую нормальный вектор .

Следовательно, и равносильное ему уравнение Ax + By + Cz + D = 0 определяет плоскость. Теорема доказана.

Рассмотрим важный частный случай построения уравнения плоскости, когда известны три точки M₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂), M₃(x₃, y₃, z₃), принадлежащие плоскости и не лежащие на одной прямой. Возьмем текущую точку M(x, y, z) плоскости и организуем три вектора

Эти векторы лежат в одной плоскости, уравнение которой и определяется. Следовательно, их смешанное произведение равно нулю, то есть

Уравнение (6) и есть уравнение плоскости, проходящей через три заданные точки M₁, M₂, M₃.

При решении задач часто используется так называемое уравнение плоскости в отрезках на осях. Пусть в общем уравнении плоскости (3) A ≠ 0, B≠ 0, C≠ 0, D≠ 0. Перенесем свободный членD в правую часть и разделим обе части уравнения на - D, тогда получим:

где 

Уравнение (7) и называют уравнением плоскости в отрезках на осях, т.к. числа a, b, c имеют простой геометрический смысл: а - абсцисса точки пересечения плоскости с осью Ох, b - ордината точки пересечения плоскости с осью Оу, с - аппликата точки пересечения плоскости с осью Oz. Действительно, точка пересечения плоскости с осью, скажем, Ох имеет ординату у = 0и аппликату z = 0. Но координаты этой точки (х,0,0) должны удовлетворять уравнению плоскости, т.е.

Отсюда получаем 

Полезно самостоятельно провести исследования общего уравнения плоскости (3), т.е. установить специфику пространственного расположения плоскости в случаях:

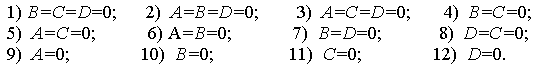
Решим теперь задачу о вычислении угла между двумя плоскостями. Угол между двумя плоскостями, точнее, один из двух смежных углов между двумя плоскостями, может быть вычислен как угол между нормальными векторами этих плоскостей. Если плоскости заданы своими общими уравнениями

то их нормальные векторы имеют вид и потому уголΘ между плоскостями находим по формуле

Условием параллельности двух плоскостей является условие

а условием перпендикулярности двух плоскостей является условие