Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Самарский национальный исследовательский университет им. ак. С.П. Королёва (бывш. СГАУ, СамГУ)

Предмет:

Сопротивление материалов

Файл:

Сопромат Лекции Филатов

.pdf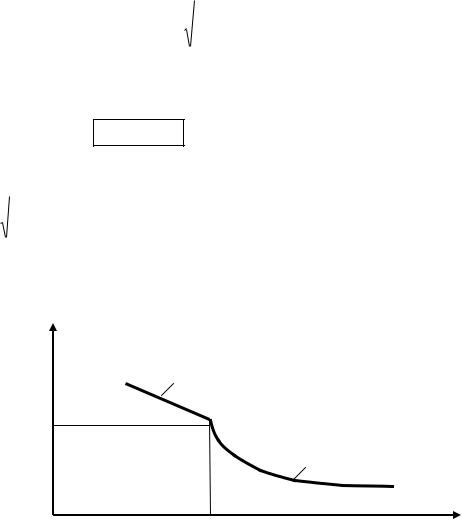

Скачиваний:

Добавлен:

29.03.2016

Размер:

1.65 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 88

С учетом рассмотренного коэффициента приведения длины стержня μ критическая сила

будет определяться формулой	F	2 EI	m in	(8.3).

	кр	( )2

8.4 Критические напряжения. Пределы применимости формулы Эйлера

С учетом величины Fкр критические напряжения определятся выражением

2 EI

m in

2 E

m in

. Так как

, то

кр

( )2 Абр

A m in

кр

im in

Выражение			называется гибкостью стержня, тогда		2 Е	.
	i			кр	2

		m in

Формула Эйлера была выведена с использованием дифференциального уравнения изогнутой

оси балки, которое справедливо в пределах упругих деформаций, поэтому критические напряжения не могут превышать предела пропорциональности, т.е.

кр 2 Е пц .2

Из этого равенства определится гибкость стержня, соответствующая пределу пропорциональности

пред	2 Е	(8.4).

	пц
Таким образом, формула Эйлера для определения критической силы может быть
использована для стержней большой гибкости, когда пред .
Критические напряжения в стержнях средней гибкости при 0			пред определяются по

формуле Ясинского кр . Здесь λ0 - предельное значение гибкости стержня, при которой

потеря устойчивости не наблюдается. Величины α, β, λ0, и λпред являются параметрами, зависящими от механических свойств материала. Например, для ст. 2, у которой пц 180 МПа ,

пред	2	2	1011	100 , λ0 =62, α =264 МПа, β=0,7 МПа. Стержни малой гибкости не теряют
	180		106

устойчивости (λ0 ≥λ), они разрушаются при достижении напряжениями предельных величин. Полный график критических напряжений представлен на рисунке

	ζкр	кр
ζтс		кр
ζтс
ζпц			кр	2	Е
			кр	2
				2

	λ0		λпред			λ

8.5 Расчеты на устойчивость с использованием коэффициента

снижения допускаемого напряжения

В расчѐтах на устойчивость необходимо рассмотреть два условия. Условие прочности

	F	0		F	у	кр
при сжатии			(α) и условие устойчивости				(b). Здесь
				Aбрутто
	Aнетто	n				nу

кр n

- напряжение предельного состояния. Если разделим равенство (b) на (α)

, то

0 n

получим

кр

. Введѐм обозначение

кр

0 n

полученный коэффициент называется коэффициентом снижения допускаемых напряжений.

Теперь условие устойчивости примет вид

. Коэффициент зависит от гибкости

Aбрутто

стержня и от материала, а его значения приводятся в виде таблиц или графиков.

Существует два вида расчѐта на устойчивостьпроверочный и проектировочный.

Проверочный расчѐт :

-известны форма сечения и его размеры, определяются площадь сечения А, момент инерции Imin,

радиус инерции i	Im in	, гибкость стержня λ		;
радиус инерции i		, гибкость стержня λ		;
m in	A		i m in
	A		i m in
-по таблицам находится ( , материал) ;
-вычисляется допускаемое напряжение ;
-сравнивается напряжение в стержне с допускаемым					F	.

					Aбрутто

Проектировочный расчѐт.

Известны форма сечения и действующая нагрузка, требуется определить размеры поперечного сечения.

Из условия устойчивости				F	записывается выражение для площади

				Aбрутто
поперечного сечения	Абрутто	F	, в котором неизвестны две величины – Абрутто и . Задача в этом

случае задача решается методом последовательных приближений, в каждом из которых выбирается новое значение .

В первой попытке наиболее часто принимают 1 0,5...0,6 , определяется Абрутто					F	,




вычисляются i	Im in	и		, по таблице находится фактическое значение	. Если
вычисляются i		и		, по таблице находится фактическое значение	. Если
m in	A		i m in	1
	A		i m in

1 значительно отличается от 1 , то и напряжение ζ будет значительно отличаться от допускаемого.

Тогда во второй попытке принимается
Тогда во второй попытке принимается	2	1	1	. В рассмотренном ранее порядке вновь находится
	2		2
			2

фактическое значение . Если отличие от рабочего напряжения от допускаемого больше 3…5%, то

выполняется третья попытка
выполняется третья попытка	3	2	2 .
	3		2
			2

Обычно требуется не более двух-трѐх попыток.

8.6 О выборе материала и рациональной формы поперечного сечения сжатых стержней

Для стержней большой гибкости (λ≥ λпред) модуль продольной упругости Е является единственной механической характеристикой, определяющей сопротивление стержня потере устойчивости. Так как эта величина для всех сталей практически одинакова, то высокопрочные стали для таких стержней применять нецелесообразно.

Для стержней малой гибкости следует применять высокопрочные стали, так как прочность в этом случае будет зависеть от предела текучести ζт.

С экономичной точки зрения наиболее рациональной будет такая форма поперечного сечения, у которой im in при определенной площади будет наибольший. Для удобства сравнения

различных сечений вводится характеристика		im in		. Приведем значения	для некоторых сечений:


			A

трубчатое сечение (α=0,95…0,8)	2,25…1,64
(α=0,7…0,8)	1,2		…1,00
уголок	0,5… 0,3
двутавр	0,41…0,27
швеллер	0,41…0,29
квадрат	0,289
круг	0,283

При проектировании сжатых стержней на устойчивость необходимо стремиться к тому, чтобы они были равноустойчивы во всех направлениях. К таким сечениям можно отнести трубчатые, квадратные или круглые сечения.

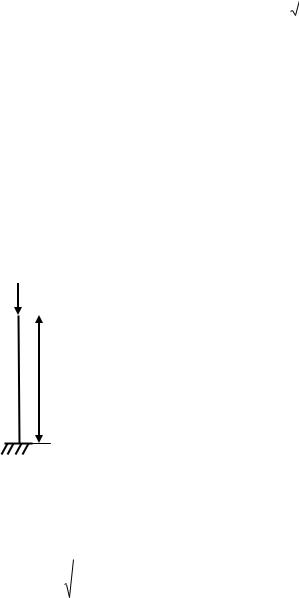
Пример. Подобрать двутавровое сечение стойки с одним защемленным концом и сжа-

F	той силой F = 400 кН; длина стойки l=1,5 м. Допускаемое
	напряжение 160 МПа . Так как в условии устойчивости
	напряжение 160 МПа . Так как в условии устойчивости
		F	нам не известно ни Aбр, ни , одной из этих

ℓ		Абр
		Абр

	величин необходимо задаться. Примем для первого
	приближения 0,5 . В этом случае необходимая площадь
	поперечного сечения стержня будет равна

А	F	400 10	3	50 10 4 м2


бр		05 160 10 6

По сортаменту выбираем двутавр № 24, с площадью А 52,6см2 . Наименьший радиус инерции

сечения im in	I m8n	=2,38 см. Соответствующая гибкость стойки		2 150	126 .
	A		im in	2,38

Коэффициент по интерполяции между значениями его из таблицы для 120 и 130 равен

0,43. Расчетное напряжением:			F	400 103	177 МПа>160 МПа. Перегрузка
0,43. Расчетное напряжением:			A	0,43 52,6 10 4	177 МПа>160 МПа. Перегрузка
			бр
составляет	177 160	100 10,7% .
составляет	160	100 10,7% .
	160

Рассмотрим двутавр № 27, а: А 54,6см2 , i		2,51см		; гибкость		2 150	120	, так как
Рассмотрим двутавр № 27, а: А 54,6см2 , i	m in	2,51см		; гибкость		2,51	120	, так как
	m in

коэффициент 0,45, то расчетное напряжение				400 10 3	162 ,5 МПа
коэффициент 0,45, то расчетное напряжение			0,45 54,6 10 4		162 ,5 МПа

Перегрузка составляет теперь 162,5 160 100 1,5% , что допустимо.

160

8.7 Продольно - поперечный изгиб

Рассмотрим нагружение прямого шарнирно закреплѐнного стержня продольной силой F и системой поперечных сил. Такой вид нагружения принято называть продольнопоперчным

изгибом. Обозначим у(z) прогиб балки в сечении c

y					абсциссой z. Воспользуемся дифференциальным
					абсциссой z. Воспользуемся дифференциальным
F				z	уравнением упругой линии балки, в котором
F				z	изгибающий момент можно рассматривать как
	уп				изгибающий момент можно рассматривать как
	уп				сумму моментов поперечных сил М п и момента
		y(z)			сумму моментов поперечных сил М п и момента
		y(z)			продольной силы F·y. Полный прогиб у
					продольной силы F·y. Полный прогиб у
z					складывается из прогиба уп от поперечных сил и
					складывается из прогиба уп от поперечных сил и
			ℓ		дополнительного прогиба у-уп от осевой силы F .
			ℓ		дополнительного прогиба у-уп от осевой силы F .
					Полный прогиб у больше суммы прогибов,

возникающих при раздельном действии поперечных и продольных сил, так как при действии только силы F прогиб равен нулю. Следовательно, в данном случае принцип независимости действия сил не применим.

d 2 y

Fy)

( 8.5 ) .

dz 2

Разделим

левую и правую части выражения (9.5) на

EI :

d 2 y

M п

(8.6)

dz 2

Так как

d 2 y

, то подставив это значение в (8.6), получим

dz 2

d 2 y

d 2 yп

dz 2

или

d 2 ( y yп )

(8.7).

dz 2

Для упрощения решения предполагается, что дополнительный прогиб у уп по длине балки изменяется по синусоиде, т.е.

у уп sin( z ) (8.8).

Это допущение позволяет получить точные результаты при действии на балку поперечной нагрузки, направленной в одну сторону.

С учѐтом (8.8) выражение (8.7) примет вид

	d 2 ( sin(	z	)
				Fy

:					.
	dz 2			EI

После двухкратного дифференцирования этого уравнения получим

					2		sin(			z			)				Fy		,
					2
																	EI
																	EI
или					2		( у		у			)		Fy				.
				2							п
														EI


Из этого равенства на ходим
							уп	2
			у				уп		2						yп
									2						yп					.
						2			F				1			F 2				.
						2			EI				1		2 EI
						2			EI						2 EI
Выражение	2	ЕI	=Fэ совпадает в формулой Эйлера, тогда
Выражение		2	=Fэ совпадает в формулой Эйлера, тогда
		2
				у=			уп					(8.9)
				у=			1	F				(8.9)
								F
								Fэ
								Fэ

Необходимо отличать эйлерову силу Fэ от критической силы Fкр, вычисляемой по формуле Эйлера для стержней большой гибкости ( пред ). Эйлерова сила Fэ не зависит от гибкости

стержня.

Из формулы (8.9), что отношение F является критерием жесткости при продольно

Fэ

поперечном изгибе. Если	F	→ 0, жѐсткость балки велика и у у		. При	F	→ 1 жѐсткость мала,
			п
	Fэ				Fэ

балка очень гибкая и у→ ∞, т.е., прогибы многократно возрастают по сравнению с уп .

Формула (8.9) достаточно точная при F≤Fкр.

Расчѐт на прочность при продольно – поперечном изгибе

Условие прочности при поперечном изгибе

М п

наиб

получено в предположении, что

внутренние усилия М п

изменяются пропорционально изменению внешних сил. Как установлено

ранее, при продольно-поперечном изгибе эта зависимость нелинейная.

Предполагая, что моменты пропорциональны прогибам, можно записать

М п

(8.10)

Fэ

Будем считать, что при переходе к предельному состоянию внешние нагрузки возрастают

пропорционально, тогда справедливы отношения

F T

М ппред

(8.11)

наиб

Здесь

и М пред нагрузки, при которых в балке напряжения достигают предела текучести

(

наиб

). Из (8.11) следует F n F ,

пред

n M

наиб .

Наибольшие напряжения при поперечном изгибе с растяжением вычисляются по формуле

наиб

М п

наиб

W (1

)

Fэ

При достижении предельного состояния они будут равны

Т FT

M п

n F

M п

F .

наиб

W (1

)

W (1 F )

Разделив правую и левую часть этого уравнения на коэффициент запаса по текучести nТ , получим

M п

наиб

W (1

nT F

)

Fэ

Так как

, то условие прочности при продольно-поперечном изгибе примет вид

наиб

. (8.12)

W (1

nT F

)

Fэ

Нелинейность в этом выражении определяется коэффициентом nT . За счѐт этой нелинейности левая часть условия прочности будет несколько меньше.

<<< < Предыдущая 1 2 3 4 5 6 78 / 88

Соседние файлы в предмете Сопротивление материалов

#
29.03.2016516.82 Кб29Расчетно-проектировочные работы по сопротивлению материалов.pdf
#
16.03.2015613.54 Кб41СБОРНИК РАСЧЕТНО-ПРОЕКТИРОВОЧНЫХ РАБОТ ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ.pdf
#
29.03.2016152.26 Кб29СОПРОМАТ 2-ая 561.docx
#
16.03.2015342.37 Кб33СОПРОМАТ 1 РГР Вариант 548.docx
#
16.03.2015147.46 Кб37Сопромат 2ргр Вариант 309.doc
#
29.03.20161.65 Mб20Сопромат Лекции Филатов.pdf
#
16.03.20151.95 Mб31Сопромат Лекции Часть 1.pdf
#
29.03.2016517 Кб18Сопромат Расчетно-проектировочные работы.pdf
#
29.03.20161.34 Mб22Справочные данные. Часть 1.pdf
#
16.03.20151.48 Mб46СПРАВОЧНЫЕ ДАННЫЕ.doc