
Сопромат Лекции Филатов
.pdfразрушение наступает при |
|
|
|
наиб |
0 . А условие прочности будет следующим: |
|
|
|
|
|
0 |
|||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
n |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
наиб |
|
|||
(5.1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
может принимать значения равные |
|
|
|
|
|
|
||||||||||||||||||||||||
Так как |
|
наиб |
1 |
или |
3 |
, то левая часть условия |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
прочности (5.1) может быть записана с использованием обобщенного закона Гука |
|
|
|
|
||||||||||||||||||||||||||||||
1 |
1 |
1 2 3 |
или |
|
3 |
|
|
|
1 |
|
1 2 3 . |
|
|
|
|
|
(5.2) |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Е |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При простом растяжении |
0 |
|
0 |
|
|
|
|
|
|
|
|
(5.3) |
|
|
||||||||||||||||||||
n |
Еn |
Е |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
После подстановки (5.2), (5.3) в условие прочности (5.1) получим |
|
|
|
|
||||||||||||||||||||||||||||||
экв II |
1 |
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.4) |
|
|
||||||||||||||
экв II |
3 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.5) |
|
|||||||||||||||
Опытная проверка этой теории показала, что она, как и первая теория, дает удовлетворительные результаты лишь для весьма хрупких материалов.
Третья теория прочности – теория наибольших касательных напряжений была предложена в 1773 году Кулоном. В этой теории в качестве критерия прочности принята величина наибольшего касательного напряжения, а нарушение прочности в общем случае сложного напряженного состояния наступает, когда наибольшие касательные напряжения достигают своего
предельного значения η0, т.е., разрушение наступает при наиб |
0 . Предельное значение η0 |
|||||||
определяется при простом растяжении. |
|
|
|
|
|
|
|
|
Условие прочности - наиб |
0 |
. |
|
|
|
|
|
(5.6) |
n |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Так как наиб 1 3 , а для одноосного растяжения |
0 |
|
0 |
|
, то из равенства |
|||
2 |
|
|
n |
|
2n |
|
2 |
|
(5.6) следует условие прочности по третьей теории |
|
|
|
|
|
|
||
эквIII 1 3 |
|
|
|
|
|
|
(5.7) |
|
Эта теория прочности хорошо подтверждается экспериментально для материалов, одинаково работающих на растяжение и сжатие. Еѐ недостатком является то, что она не учитывает влияния на
прочность материала среднего по величине главного напряжения ζ2
|
Если материал не одинаково сопротивляется растяжению, сжатию, то Мор предложил |
|||||||
следующее условие прочности, называемое теорией Мора |
|
|||||||
|
|
|
1 к 3 |
, |
(5.8) |
|||
где |
к |
Тр |
для пластических, |
к |
|
вр |
для хрупких материалов, а ζТр , ζТс, ζвр , |
ζвс пределы |
|
|
|||||||
|
|
Тс |
|
|
вс |
|
||
текучести и пределы прочности материала при растяжении и сжатии, |
|
|||||||
|
Использование этой теории затруднено, так как не для всех материалов есть данные для |
|||||||
определения коэффициента «k». |
|
|
|
|
|
|||
|
Четвѐртая теория прочности – теория октаэдрических касательных напряжений |
|||||||
(энергетическая теория прочности), предложенная Губертом в1904 году. |
|
|||||||
|
Условие прочности с указанным критерием |
|
||||||
|
|
|
окт окт0 |
IY |
( 5 .9) |
|||
Левая часть этого выражения определяется известной формулой
41

|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
окт |
|
|
12 |
|
22 32 |
1 2 |
2 3 1 3 |
(5.10) |
||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
3 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для правой части при одноосном растяжении ζ1= ζ, ζ2= ζ3=0, тогда |
|
||||||||||||||||||
|
|
|
|
|
|
|
окт0 |
IY |
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
окт0 |
|
|
, |
|
|
|
2 |
|
|
|
|
(5.11) |
|||||||
3 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|||
После подстановки (5.10), (5.11) в выражение (5.9) получим формулу, определяющую условие прочности по четвертой теории предельного напряженного состояния.
|
|
|
|
|
|
|
|
|
ζэквIV= |
2 |
2 |
2 |
|
|
|
(5.12) |
|
1 |
2 |
3 |
1 2 |
2 3 |
1 3 |
|
Контрольные вопросы
1.Что называется напряженным состоянием в точке?
2.Сколько и какие компоненты напряжений определяют напряженное состояние в точке?
3.В чем заключается закон парности касательных напряжений?
4.Какие площадки называются главными?
5.Какие напряжения называются главными?
6.Виды напряженного состояния?
7.Как вычисляются напряжения на произвольных площадках, повернутых от главных на угол a (альфа), аналитическим способом при плоском напряжѐнном состоянии?
8.Как вычисляются напряжения на произвольных площадках, повернутых от главных на угол альфа, графическим способом при плоском напряжѐнном состоянии?
9.Как определяются главные напряжения и положение главных площадок аналитическим способом при плоском напряжѐнном состоянии?
10.Как определяются главные напряжения и положение главных площадок графическим способом при плоском напряжѐнном состоянии?
11.Обобщенный закон Гука для главных площадок при объѐмном напряжѐнном состоянии?
12.Обобщенный закон Гука для произвольных площадок при объѐмном напряжѐнном состоянии?
13.Условие прочности по третьей теории прочности?
14.Условие прочности по четвѐртой теории прочности?
42
6ИЗГИБ
6.1Основные понятия об изгибе
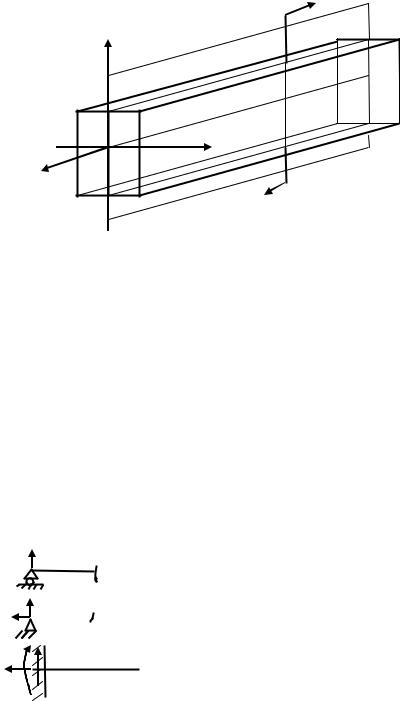
Прямой брус испытывает деформацию изгиба, если он нагружен силами или парами сил в плоскости, проходящей через ось бруса, а сами силы или пары сил действуют перпен-дикулярно этой оси (рис. 5.1). Брус под действием этих сил изогнѐтся, его ось искривится, а в поперечных сечениях появятся изгибающий момент М и поперечная сила Q.
У
F
0 |
Х |
Z |
|
m Рис.6.1
Брус испытывает прямой изгиб, если плоскость действия моментов совпадает с одной из главных плоскостей жѐсткости. Главные плоскости жѐсткости – это плоскости, проходящие через ось бруса и одну из главных центральных осей инерции (YOZ – плоскость максималь-ной жѐсткости, XOZ– плоскость минимальной жѐсткости).
Если плоскость действия момента и плоскость перемещений (деформаций) совпадают, то такой изгиб называется плоским.
Если изгибающий момент в поперечном сечении бруса является единственным силовым фактором, то такой изгиб называется чистым.
Если наряду с изгибающим моментом в поперечном сечении бруса действует и поперечная сила, то изгиб называется поперечным.
Прямолинейный брус, работающий на изгиб, называется балкой.
6.2 Опорные устройства балок и их типы
Действие внешних сил, приложенных к балке, замыкается на опорах, которые исключают еѐ перемещение как твердого тела. Конструктивные формы опор разнообразны, но в расчетных схемах они приводятся к трем основным типам:
|
V |
|
|
Шарнирно-подвижная опора, в которой возникает только одна |
|
V |
|
|
вертикальная реакция |
|
|
|
Шарнирно-неподвижная опора, в которой возникает две реакции |
|
Н |
|
|
|
|
|
V |
|||
М |
|
|||
|
|
Жесткое защемление (заделка), в котором возникает три реакции: |
||
H |
|
|
вертикальная, горизонтальная и опорный момент. |
|
43
6.3 Определение реакций
Определение опорных реакций изучается в теоретической механике. Поэтому рассмотрим только некоторые практические вопросы.
Опоры балок обычно обозначаются буквами, например, А, В, С, показывается воз-можное направление реакций, действующих в этих опорах. Обычно их направляют вверх от опоры.
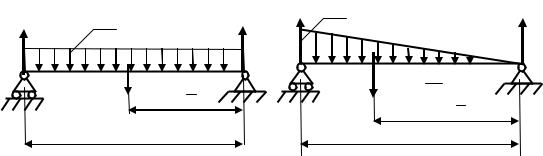
Если на балку действует распределѐнная нагрузка, то она заменяется равнодействую-щей (Σq ), величина которой находится как площадь грузовой эпюры, прикладывается она в центре тяжести этой эпюры. В качестве примера рассмотрим равномерно распределѐнную нагрузку и нагрузку, изменяющаяся по линейному закону. Грузовые эпюры этих нагрузок представляет собой соответственно прямоугольник и прямоугольный треугольник Их равнодействующие и точки приложения показаны на рисунках (6.5) и (6.6).
RA |
q |
|
RB |
|
RA |
q |
|
|
|
|
|
|
RB |
||||
|
|
|
|
|
|
|
|
|
А |
q q |
|
|
B |
А |
q |
q |
B |
|
|
|
2 |
|||||
|
|
|
|
|
|
2 |
||
|
|
2 |
|
|
|
|
|
3 |
ℓ |
ℓ |
Рис.6.5 |
Рис.6.6 |
Согласно правилам теоретической механики для определения реакций плоской системы сил используется три уравнения статики.
∑Z =0 - сумма проекций всех внешних сил на ось балки должна равняться нулю. При изгибе это уравнение выполняется тождественно, так как все силы действуют перпендикулярно оси, поэтому в балках горизонтальные реакции отсутствуют.
∑У=0 – сумма проекций всех внешних сил на направление, перпендикулярное оси балки должна, равняться нулю.
∑M=0 – сумма моментов всех внешних сил относительно центра тяжести любого произвольного сечения балки должна равняться нулю.
Целесообразно для определения реакций использовать уравнения моментов относи-тельно шарнирных опор.
Условие ∑У=0 наиболее часто используется для проверки правильности нахождения реакций.
6.4 Внутренние усилия при изгибе
Рассмотрим в условиях статического равновесия балку, нагруженную сосредоточенной силой
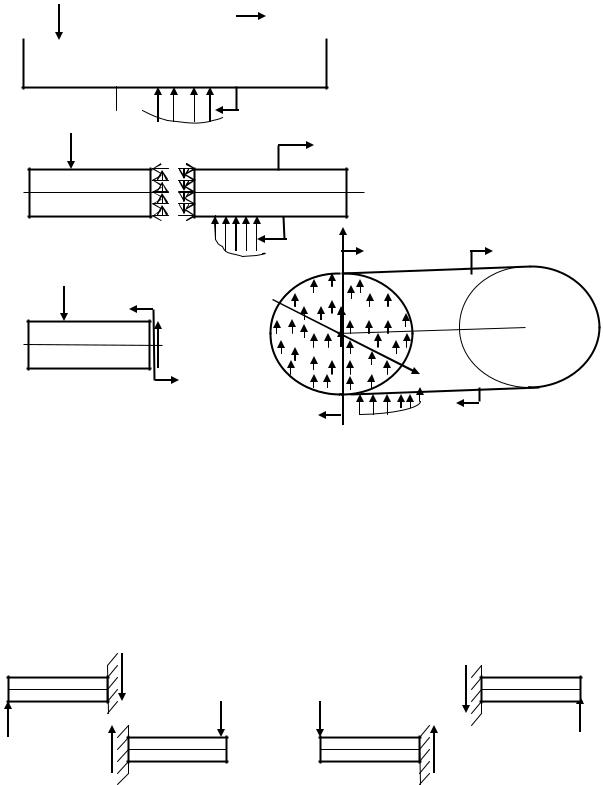
F, распределенной нагрузкой с интенсивностью q=q(z) и парой сил m (рис.6.7 а). Применяя метод сечений, разделим брус мысленно на две части (рис. 6.7 в). Для того чтобы каждая из частей находилась в равновесии, в сечении необходимо приложить поперечную силу Q и изгибающий момент М (рис.6.7 с). Эти силовые факторы определяются из уравнений равновесия одной из частей бруса по следующим правилам: поперечная сила Q в каком либо
44
а) F |
|
а |
|
М |
|
|
а 
в) F |
q=q(z) |
М |
|
|
|
У |
Мправ |
|
|
|
|
|
|
q=q(z) |
|
с) |
F |
Млев |
|
|
|
Qправ |
|
|
|
С |
|
|
|
Qлев |
|
Х
Рис.6.7
сечении балки равна сумме проекций всех внешних сил, расположенных по одну сторону от сечения, на направление перпендикулярное оси балки; изгибающий момент М в каком либо сечении балки равен сумме моментов всех внешних сил, расположенных по одну сторону от сечения относительно центра тяжести этого сечения.
Правила знаков при определении поперечной силы: поперечная сила Q считается положительной, если внешняя сила стремится повернуть рассматриваемую часть балки относительно сечения по часовой стрелке, если внешняя сила стремится повернуть рассматрива-емую часть балки против часовой стрелки, то Q принимается отрицательной. Эти правила знаков можно представить схемой (рис.6.8)
|
Qлев>0 |
|
|
Qправ<0 |
|
|
|
F |
|
|
|
|
|
|
F |
|
F |
|
F |
|
|
|
|
|
Qправ>0 |
|
|
Рис.6.8 |
Qлев<0 |
|
|
|
|
Правила знаков при определении изгибающего момента: если внешние силы изги-бают балку выпуклостью вниз, то изгибающий момент считается положительным, если выпуклостью вверх - отрицательным (рис. 5.9).
45
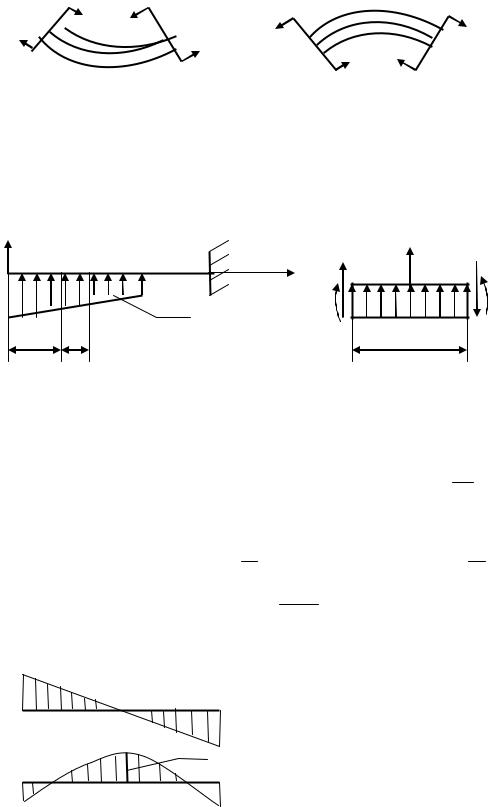
М<0
М>0
Рис. 6.9
6.5 Дифференциальные зависимости при изгибе между q, Q, M
Вырежем из балки на участке с распределенной нагрузкой (рис.6.10 а) элемент длиной dz , по торцам которого будут действовать внутренние усилия (рис.6.10 б). В силу малости
У |
|
Q(z) |
|
Q(z)+ dQ(z) |
|
|
q·d |
||
|
|
Z |
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
M(z) |
|
M(z)+dM(z |
|
|
q=q(z) |
|
|
Z |
dz |
|
dz |
|
|
|
|
|
|
|
а) |
Рис. 6.10 |
б) |
|
|
|
|
участка
dz интенсивность распределенной нагрузки на нем можно принять постоянной, тогда еѐ равнодействующая будет равняться q·dz. Рассмотрим равновесие этого элемента
∑У = 0, Q(z) + q·dz –Q(z) - dQ(z) =0, из этого уравнения следует, что dQdz q , т.е., производная от
поперечной силы Q по длине балки z равна интенсивности распределенной нагрузки q.
В качестве второго уравнения равновесия рассмотрим сумму моментов всех сил относительно правого торца: - M(z) - Q(z)·dz - q·dz· dz2 + M(z) + dM(z) =0, так как q·dz· dz2 величина второго порядка
малости, то ею можно пренебречь, тогда dM ( z ) Q( z ) , т.е., производная от изгибающего момента по dz
длине балки z равна поперечной силе Q(z).
|
|
|
|
|
|
|
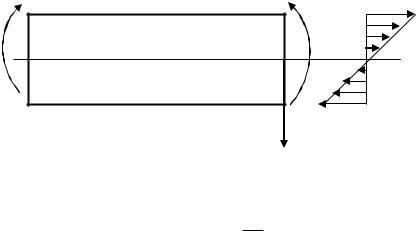
Полученные соотношения выведены при направлении |
|||||
|
|
|
|
|
|
|
оси Z |
слева направо (в правой системе координат). При |
||||
+ |
|
|
|
|
|
|
противоположном еѐ направлении правые части |
|||||
|
_ |
|
|
|
полученных дифференциальных зависимостей изменят |
|||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
dM ( z ) |
|
|
||
|
|
|
|
|
|
Q |
знак: |
dQ |
q , |
Q |
. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Mmax |
|
|
dz |
|
dz |
( z ) |
|
||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
Рассмотренные дифференциальные зависимости |
|||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
M |
используются для контроля эпюр Q и М |
|||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
1. Если на участке балки Q>0, то момент на этом |
|||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||
|
Рис. 6.11 |
|
|
|
|
|
участке возрастает, если Q<0, то момент убывает, если |
|||||
|
|
|
|
|
|
Q=0, то М= const. |
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
2. Если эпюра Q плавно меняет знак |
||||
|
|
|
|
|
|
|
(рис. 6.11), то момент в этом сечении принимает |
|||||
|
|
|
|
|
|
|
экстремальное значение. При смене знака с плюса на |
|||||
46
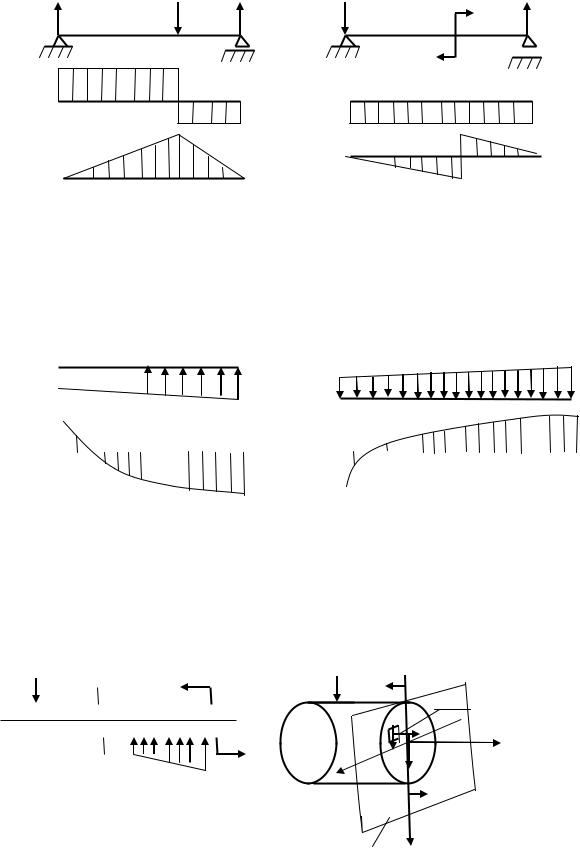
минус он будет максимальным, при смене знака с минуса на плюс - минимальным.
3. В сечении балки, где имеется сосредоточенная сила, на эпюре Q будет скачок, равный по величине этой силе, а на эпюре М излом (рис.6.12).
4. В сечении балки, где имеется сосредоточенный момент, на эпюре моментов будет скачок, равный по величине этому моменту (рис.6.13).
F |
|
|
М |
+ |
|
|
|
_ |
|
+ |
Q |
|
Q |
|
|
|
|
|
|
|
|
|
М |
|
М |
|
|
Рис. 6.12 |
|
Рис. 6.13 |
|
5.На участке с распределенной нагрузкой эпюра моментов описывается параболой с выпуклостью на встречу нагрузке (рис.6.14).
6.Эпюры изгибающих моментов, согласно принятым правилам знаков, всегда строятся на сжатых волокнах.
q> 

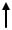

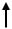
q<0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2 M |
|
|
|
|
|
|
|
d 2 M |
q |
|||
|
q >0 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
dz 2 |
||||||
|
dz 2 |
|
|
Рис.6.14 |
|||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
6. Эпюры изгибающих моментов, согласно принятым правилам знаков, всегда строятся на сжатых волокнах.
6.6 Напряжения при изгибе
|
|
|
|
|
|
|
Рассечѐм балку |
а |
|
|
|
|
|
|
плоскостью а-а и в еѐ |
|
|
|
|
|
dА |
левой части выделим |
|
|
|
|
|
|
η |
||
|
|
|
|
|
ζ |
элемен-тарную площад- |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Z |
ку dА, на котор-ой |
а |
|
|
|
|
|
||
|
|
Х |
|
|
Q |
будут дейст-вовать |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
нормаль-ные и |
|
Рис. 6.15 |
|
|
касатель-ные |
|||
|
|
У |
напряжения. |
||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
плоскость а-а |
|
|
|
||
47
|
|
|
|
|
|
|
Рассечѐм балку |
а |
|
|
|
|
|
|
плоскостью а-а и в еѐ |
|
|
|
|
|
dА |
левой части выделим |
|
|
|
|
|
|
η |
||
|
|
|
|
|
ζ |
элемен-тарную |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Z |
площадку dА, на котор- |
а |
|
|
|
|
|
||
|
|
Х |
|
|
Q |
ой будут действовать |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
нормальные и |
|
Рис. 6.15 |
|
|
касательные |
|||
|
|
У |
напряжения. |
||||
|
|
|
|
|
|
||
|
|
|
|
|
|
Равнодействущая |
|
|
|
плоскость а-а |
|
|
|||
|
|
|
|
элементарных усилий |
|||
|
|
|
|
|
|
|
|
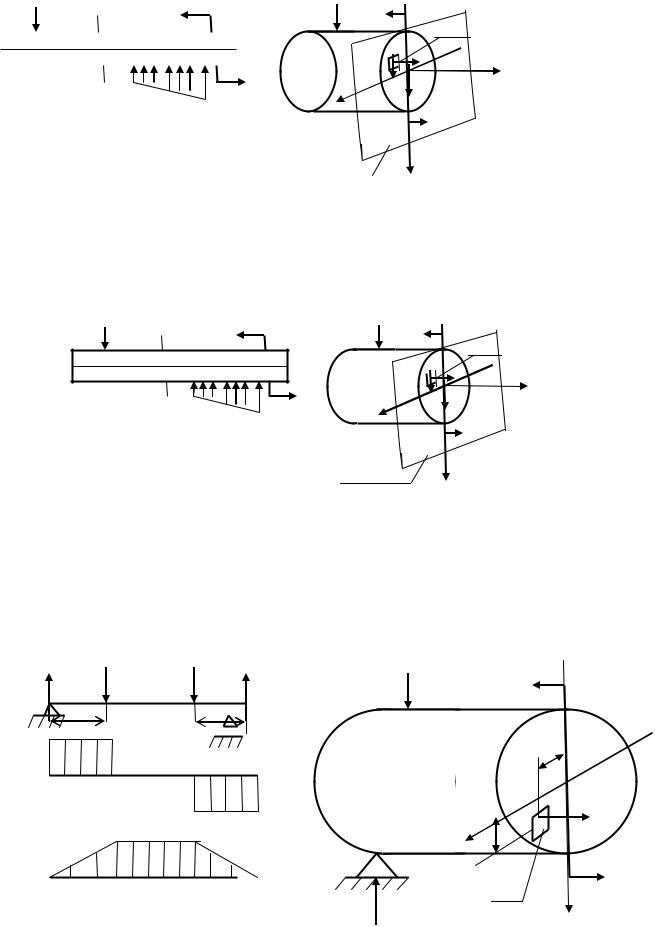
ζdА будет равняться изгибающему моменту М, а равнодействующая ηdА будет равна поперечной силе Q.
Таким образом, нормальные напряжения в балке зависят только от момента, а ка-сательные от силы Q (рис.6.15)
а |
|
|
dА |
|
|
η |
|
|
|
ζ |
|
|
|
|
|
а |
|
|
Z |
Х |
|
Q |
|
|
|
||
|
|
|
М |
|
Рис. 6.15 |
|
У |
|
|
|
|
|
плоскость а- |
|
|
6.6.1 Нормальные напряжения при чистом изгибе
При чистом изгибе Q=0, М=const. Такой вид деформации будет на участке между силами F балки, представленной на рис. 6.16 а.
Изгиб изучается в главных центральных осях, поэтому оси Х и У (рис.6.16 б) – главные
RА=F |
|
|
RВ= F |
|
|
|
|
F |
F |
F |
|
|
|
|
|
|
|
|||
|
|
|
|
М |
|
|
|
|
|
|
|
|
|
|
α |
α |
|
|
|
|
Q |
+ |
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
_ |
|
|
|
|
|
|
|
RА |
|
ζ |
|
|
|
|
|
У |
|
М |
|
|
|
Х |
у |
|
|
|
|
|
|
|
|
|
а) |
|
|
б |
dА |
|
|
|
Рис. |
|
У |
||
|
|
|
|
|
||
|
|
|
|
|
|
48
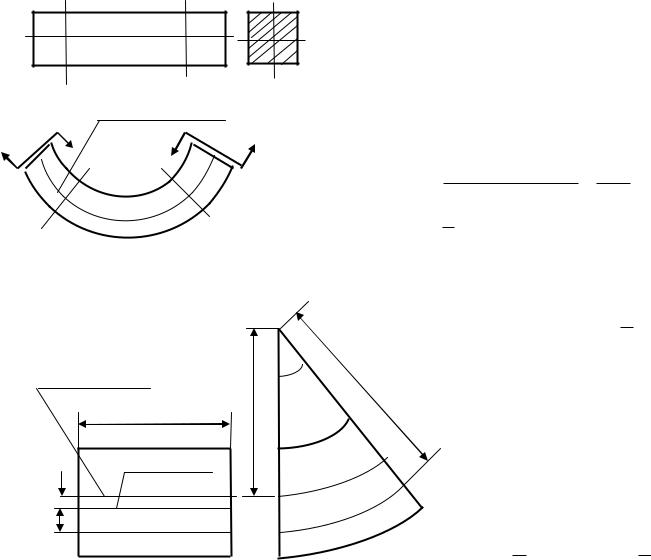
центральные. Чтобы согласовать знак нормальных напряжений со знаком изгибающего момента ось |
|||||||||
У направлена вниз. |
|
|
|
|
|
|
|||
|
Запишем уравнения равновесия левой части рассматриваемой балки (рис.6.16,б). |
|
|||||||
ΣΧ=0 (6.1), ΣУ=0 (6.2), ΣZ= dA =N =0 (6.3), ΣMх= dAу =М (6.4), Mу= dAх =0 (6.5), ΣMz= 0 |
|||||||||
|
|
|
А |
|
А |
|
А |
|
|
(6.6). |
|
|
|
|
|
|
|
|
|
Уравнения (6.1), (6.2), (6.6) выполняются тождественно. Оставшиеся уравнения (6.3), (6.4), (6.5) |
|||||||||
имеют бесчисленное множество решений, т.к. они могут удовлетворятся при различных законах |
|||||||||
распределения нормальных напряжений по сечению. Таким образом, определение этих напряжений |
|||||||||
является статически неопределимой задачей. Для еѐ решения рассмотрим закономернои деформаций |
|||||||||
при изгибе на примере бруса с прямоугольным сечением, которые при чистом изгибе легко |
|||||||||
обнаружить экспериментальным путѐм |
|
|
|
|
|
||||
|
Поперечные сечения плоские и перпендикулярные к оси до деформации, остаются плоскими |
||||||||
и перпендикулярными к оси балки после деформации. Часть волокон растягивается, часть |
|||||||||
сжимается. Между ними имеются волокна, которые не изменяют своей длины, они образуют |
|||||||||
1 |
|
|
2 |
|
нейтральный слой (рис.6.17). Линия пересечения |
||||
|
|
|
|
|
нейтрального слоя с поперечным сечением называется |
||||
|
|
|
|
|
нейтральной линией. |
|
|
|
|
|
|
|
|
|
Рассмотрим элемент балки длиной dz. (рис. 6.18). |
||||
1 |
|
|
2 |
|
Примем условно левый его торец за непод-вижный, тогда |
||||
|
|
|
правый повернѐтся относительно его на угол dΘ. Так как |
||||||
|
|
|
|
|
|||||
|
|
Нейтральный слой |
|
нейтральный слой своей длины не меняет, то CD=C1D1 = |
|||||
|
|
|
|
|
ρdΘ. Деформация произвольного отрезка АВ=dz, взятого |
||||
|
1I |
|
2I |
|
на рассто-янии y от нейтрального слоя, найдется из |
||||
|
|
|
выраже-ния: εАВ= |
( у е)d d |
у е |
|
|||
|
|
|
Рис.6.17 |
|
, т.е. |
||||
|
|
|
|
|
|
|
|
|
|
1I |
|
|
2I |
|
ε |
1 (е у) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь е -расстояние нейтрального слоя от центральной |
||||
оси х. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По закону Гука для одноосного |
|||
|
|
|
|
|
|
растяжения Е Е 1 |
( у е) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dΘ |
|
(6.7). |
|
|
|
Нейтральный слой |
ρ |
ρ+е+у |
Это выражение представляет |
||||||
|
|
|
|
||||||
|
|
|
|
|
|
уравнение совместности деформаций, |
|||
|
|
|
dz |
|
|
полученное на основе гипотезы |
|||
|
|
|
|
|
|
плоских сечений и линейного |
|||
|
|
|
Ось балки |
|
D1 |
напряженного состояния в |
|||
|
|
|
|
|
поперечном сечении балки. Теперь |
||||
|
|
|
|
|
|
||||
е |
С |
|
D |
С1 |
В1 |
уравнения равновесия (6.3), (6.4), (6.5) |
|||
|
|
|
|
|
с учетом формулы (6.7) будут иметь |
||||
|
|
|
|
|
|
||||
у |
|
|
|
А1 |
|
единственное решение. |
|
||
|
А |
|
В |
|
dA |
E ( y e)dA 0 , |
E ≠0, |
||
|
|
|
|
||||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
А |
A |
|
|
|
|
|
|
|
|
следовательно, |
|
|
|
( y e)dA ydA edA 0 . Каждый из последних двух интегралов должен равняться нулю. |
|||||||||
A |
|
A |
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
49 |
Первый интеграл представляет статический момент площади уdA Sx 0, так как он равен нулю,
A
то нейтральная линия совпадает с центральной осью Х, во втором интеграле edA eA 0
|
|
|
|
|
A |
|
|
|
А≠0,следовательно, е 0 , т.е., |
нейтральный слой проходит через ось бруса. В этом случае |
Е |
у |
|||||
|
||||||||
|
|
|
|
|
|
|
||
(6.8). |
|
|
|
|
|
|
|
|
dAх = |
Е |
хуdA 0 |
, xydA x y |
0 . Центробежный момент инерции равен нулю, поэтому |
||||
|
||||||||
А |
А |
A |
|
|
|
|
||
оси Х,У являются главными центральными.
|
Уравнение (6.4): |
Е |
y 2 dA М , |
так как у2 dA x , то |
1 |
|
M |
|
(6.9), |
|
|
|
|
|
|
|
|||||||
|
|
A |
А |
|
EI x |
|
|
|
|
||
1 |
- кривизна изогнутой оси балки. ЕI х - жѐсткость при изгибе. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставив значение кривизны (6.9) в уравнение (6.8), получим |
|
М |
у (6.10). Это |
|||||||
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
х |
|
формула для нормальных напряжений при чистом изгибе. Из неѐ следует, что по ширине сечения нормальные напряжения не меняются, а по высоте (вдоль оси У) они меняются по линейному закону
(рис.6.19).
М>0
Рис.6.19
У
ζ |
- |
+ |
Максимальные напряжения будут при у = уmax, т.е., m ax |
M |
y m ax, но |
I x |
W x |
- момент |
|
I x |
ym ax |
|||||
|
|
|
|
сопротивления изгибу, тогда m ax M . Эта формула позволяет записать условие прочности
Wx
при изгибе по нормальным напряжениям при условии, что материал одинаково
сопротивляется растяжению, сжатию: наиб |
|
/ M / наиб |
≤ [ζ]. (6.11) |
|
|||
|
|
Wx |
|
Из этого условия прочности может быть решен вопрос о размерах поперечного сечения
балкиWx ≥ |
M |
наиб |
(6.12) и о еѐ грузоподъѐмности |
|
М |
|
|
Wx (6.13) |
|
|
|
||||||
|
|
|
|
|||||
|
|
|
наиб |
|||||
|
|
|
|
|
|
|
|
|
6.6.2 Напряжения при поперечном изгибе
При поперечном изгибе в сечении бруса кроме изгибающего момента действует и поперечная сила. Следовательно, в этом случае в поперечных сечениях бруса возникают не только нормальные, но и касательные напряжения.
50
