
Сопромат Лекции Филатов
.pdf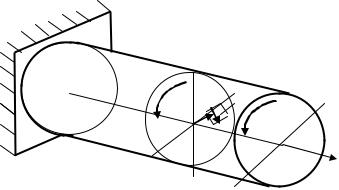
момента М на угол поворота θ, т.е., А М , |
N |
M |
, |
но |
-угловая скорость, следовательно, |
||||||
|
|||||||||||
|
|
|
|
t |
|
|
t |
|
|
|
|
N= Мω .Угловая скорость определится по формуле |
|
2 n |
|
n |
, с учѐтом которой момент |
||||||
60 |
30 |
||||||||||
|
|
|
|
|
|
|
|
||||
определится из выражения |
|
|
|
|
|
|
|
|
|||
М= 9,55 |
N |
. |
|
|
|
|
|
|
|
(7.4). |
|
|
|
|
|
|
|
|
|
||||
n
Здесь N – передаваемая валом мощность кВт , n – число оборотов вала в минуту, М – внешний момент на валу кНм .
7.2.3 Напряжения и деформации при кручении круглого вала. Расчет на прочность и жѐсткость
Рассмотрим брус круглого сечения, нагруженный парами сил в плоскости торцевого сечения (рис.7.7). В поперечных сечениях этого бруса возникает постоянный крутящий.момент
|
|
|
Мкр =М или Мкр = dA . |
(7.5). |
||
|
|
|
|
|
А |
|
Это уравнение позволит определить касательные |
||||||
напряжения, если известен их закон распределения |
||||||
по площади сечения. На основании результатов |
||||||
М |
dА |
|
|
1) поперечные сечения бруса |
||
|
|
|||||
ρ |
|
|
плоские и нормальные к оси |
|||
|
|
|
|
|||
η |
|
М |
|
до деформации остаются |
||
|
|
|
плоскими и нормальными |
|||
|
|
|
|
|
||
|
|
|
|
Z |
после деформации, |
т.е. при |
|
|
|
|
кручении круглых валов |
||
|
|
|
|
|
||
Рис.7.7 |
|
|
|
|
справедлива гипотеза |
|
мя сечениями в процессе деформации кручения не изменяется (εz = 0);
3) поперечные сечения в своей плоскости не деформируются, т.е., радиусы не искривляются и не изменяют своей длины, они лишь поворачиваются как жесткие диски (εх=0, εу=0).
На основании этих допущений ζх =ζу =ζz =ηху =0, поэтому в поперечных сечениях будут
действовать только касательные напряжения ηzx и ηzу, следовательно, при кручении брус испытывает деформацию чистого сдвига.
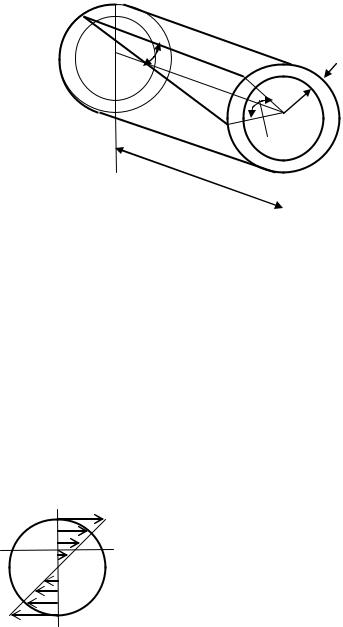
Двумя поперечными сечениями выделим из вала элемент длиной dz , а из него затем выделим элементарное кольцо с радиусами ρ и ρ + dρ (рис. 7.8). Будем считать левое торцевое сечение неподвижным, тогда правое торцевое сечение кольца повернется под действием крутящего момента относительно левого на угол dθ. Образующая цилиндра АВ при этом повернѐтся на угол γ и займет положение АВ . С одной стороны дуга В В / =ρdθ, с другой - В/ В/ = γdz, следовательно,
|
d |
|
|
||
|
. |
|
(7.6) |
||
dz |
|
||||
Угол γ – это угол сдвига цилиндрической поверхности, а величина |
d |
Θ называется |
|||
dz |
|||||
|
|
|
|
||
относительным углом закручивания (аналогично ). |
|
|
|||
|
|
|
|
|
|
61
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По закону Гука для сдвига η=Gγ, |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
γ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
|
d |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
|
dρ |
|
|
|
|
|
|
|
|
|
|
G |
|
dz |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
|
|
|
|
|
|
откуда следует |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
d |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7.7) |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dθ |
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dz |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
В/ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя (7.7) в уравнение (7.5), получим |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M kр |
G |
d |
dA. |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dz |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Рис. 7.8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
dz |
|
|
|
|
|
dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Так как |
d |
const , то M |
|
G |
d |
|
|
|
|
2dA. Учитывая, что |
|
|
|
2 dA I |
|
|
получим |
|
|||||||||||||||||||||||||||||||||||||||
|
|
k |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
M |
|
G |
d |
|
I |
|
, |
d |
|
|
M кр |
|
(а), d |
|
Mкрdz |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
k |
|
dz |
|
dz |
|
GI |
|
|
|
|
GI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Из последнего выражения следует формула угла закручивания |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М к dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
GI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7.8) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Если крутящий момент Мк и жесткость вала GІρ |
по его длине не изменяются, то |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М |
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
(7.9) |
||||||
η max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
GI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
Вернѐмся к выражению (7.7). Используя уравнение (а), получим формулу |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
касательных напряжений при кручении круглого вала |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
М к |
= |
|
M K |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7.10) |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
GI |
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
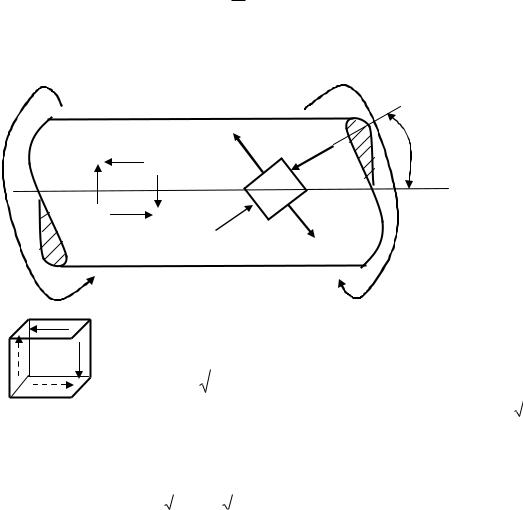
Согласно этой формуле касательные напряжения в поперечном |
сечении |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
вала распределяются вдоль радиуса по линейному закону, достигая наибольшей |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
Рис. 7.9 |
|
|
величины в точке наиболее удаленной от оси бруса (рис.7.9). |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M k |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
Согласно (7.10): |
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
. |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
m ax |
|
|
|
m ax |
m ax |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m ax |
|
|
|
|
||||
Введя обозначение |
|
I |
|
|
W (момент сопротивления сечения при кручении), получим |
||||||||||||||||||||||||||||||||||||||||||||||||||||
m ax |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m ax |
|
M k |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 4 |
, |
|
|
|
|
|
|
d |
|
|
|
|
d |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Для круглого сечения I |
|
|
|
m ax |
|
|
|
, W |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32 |
|
|
|
|
2 |
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Материал вала возле оси недогружен, поэтому применяют пустотелые валы. При равных площадях поперечных сечений и одинаковом крутящем моменте в пустотелом вале напряжения будут меньше, а при равных напряжениях в пустотелом вале крутящий момент будет больше.
62
|
|
|
|
D4 |
|
d 4 |
D4 |
|
|
|||
Для такого вала |
I |
|
|
|
|
|
|
|
(1 4 ) , |
|
|
|
|
|
|
|
|
||||||||
|
|
|
32 |
|
32 |
32 |
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
где D- наружный диаметр, d – внутренний диаметр вала, |
D |
, |
||||||||||
d |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
W |
I |
D3 (1 4 ) . |
|
|
||||||
|
|
|
|
|
||||||||
|
|
|
|
|
D |
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2
Расчѐт на прочность круглого вала может выполняться по двум методам: по допус-каемым напряжениям и по допускаемым нагрузкам. В данном разделе рассмотрим первый методметод допускаемых напряжений, так как он наиболее часто используется на практике.
Мкр |
|
|
|
|
|
|
|
|
|
|
|
|
Мкр |
|
|
|
|
|
|
|
|
|
|
|
|
Предельное состо-яние в |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
опасной точке, расположенной |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на повер-хности вала (рис.7.10) |
||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
45 |
|
|
|
достигается в сечении с |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
наибольшим крутящим |
|||||||||||
m ax |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
моментом. В этой точке будет |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
напряжѐнное сос-тояние чистого |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сдвига, т.е. по граням |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
элементарного параллелепипеда |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
действу-ют только касательные |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
напряжения (рис.7.11). В |
||||||
|
|
|
|
|
|
|
|
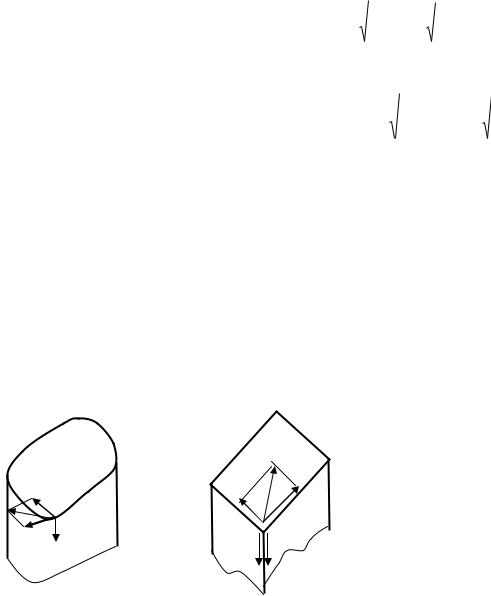
Рис.7.10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
этом случае |
|||||||
|
|
|
1 m ax, 2 0, 3 m ax. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Условие пластичности по энергетической теории предельного напряжѐнного |
||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
|
|
|
состояния определяется выражением |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2 |
3 |
2 |
|
2 |
|
3 |
|
1 |
|
Т |
. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
3 |
1 |
2 |
|
3 |
|
|
|
|
|
|
|||||
Рис.7.11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для рассматриваемого случая оно примет вид |
|
3 max = Т . |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Для безопасной работы вала должно выполняться условие |
max |
T |
,т.е. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nT |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
m ax |
, где |
T |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
3 nT |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, условие прочности при кручении круглого вала запишется формулой:
|
|
|
|
М кр |
|
наиб |
. |
(7.11) |
|
|
m ax W
Из него следуют формулы для назначения размеров поперечного сечения вала и определения грузоподъѐмности:
W |
|
|
M kp |
|
наиб |
|
|
|
|
|
|
W |
|
|||
|
|
|
, |
М |
|
|
|
|
|
(7.12) |
||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
кр |
|
наиб |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
Условие жесткости |
|
|
|
|
|
M k |
|
. |
(7.13) |
|||||||
|
|
|
|
GI |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Произведение GIρ называется жесткостью при кручении. Іρ – полярный момент инерции, G – модуль упругости при сдвиге.
Если вал имеет несколько участков, то угол закручивания θ на всей его длине найдется как сумма углов закручивания на всех участках θi :
63
|
|
|
|
|
|
|
|
|
|
|
|
|
θ =∑ θi =∑ |
М кi i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(7.14) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
GI I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Пример: подобрать размеры круглого и кольцевого сечения вала, передающего мощ-ность 80 |
||||||||||||||||||||||||||||||||||||||||||
кВт при числе оборотов n=600об/мин, если |
60МПа , α = |
d |
|
0,8 . Сравнить массы валов с |
||||||||||||||||||||||||||||||||||||||||
D |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
указанными сечениями. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Мк = 9,55 |
N |
9,55 |
|
80 |
|
1,273kHм , W |
|
M k |
|
наиб |
|
|
1,273 103 |
|
|
21,22см2 . |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
60 106 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
600 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Для круглого сечения : W |
|
|
|
|
|
|
|
16W |
|
|
|
|
16 21,22 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
, тогда |
d 3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
4,76см |
, |
|||||||||||||||||||||
|
|
16 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
площадь сечения А = |
d 2 |
|
4,76 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
4 |
|
4 |
17,82см2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Для кольцевого сечения: W |
|
(1 |
4 |
) , |
|
D |
3 |
|
|
|
16W |
|
|
3 |
|
|
16 21,22 |
|
5,67см , |
|||||||||||||||||||||||
|
|
16 |
|
|
|
(1 4 ) |
|
|
(1 0,84 ) |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
d 0,8D 0,8 5,67 4,54см , площадь сечения |
А= |
(D2 |
d 2 ) |
|
(5,672 4,542 ) 9,1см2 . |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
Массы валов будут пропорциональны площадям поперечных сечений |
|
|
||||||||||||||||||||||||||||||||||||||||
|
mкруг |
|
Акруг |
|
17,82 |
2 |
|
, т.е., полый вал будет почти в два раза легче сплошного вала. |
||||||||||||||||||||||||||||||||||||
|
mкольц |
Акольц |
|
|
9,1 |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
7.2.4 Кручение брусьев некруглого поперечного сечения.
Напряжения и перемещения в вале прямоугольного поперечного сечения
Задачи определения напряжений и деформаций при кручении брусьев некруглого поперечного сечения нельзя решить методами сопротивления материалов. Эти задачи
|
|
|
|
|
рассматриваются в теории упругости. Причина |
|
|
|
|
|
этого в том, что у таких брусьев гипотеза |
|
|
|
|
|
плоских сечений не применима, так как |
· |
|
|
|
2 |
поперечные сечения заметно искривляются, что и |
n |
А |
1 |
приводит к существенному изменению |
||
|
|
|
распределения напряжений. |
||
|
|
|
|
||
|
|
|
|
|
Отметим некоторые закономерности |
|
|
|
|
распределения напряжений в сечениях некруглой |
|
|
|||||
|
T |
n |
формы, а затем приведем готовые решения, |
||
|
|
|
2 |
1 |
|
|
|
а) |
б) |
|
полученные методами теории упругости для |
|
|
|
Рис. 7.12 |
|
некоторых форм поперечных сечений. Прежде |
|
|
|
|
всего, покажем, что касательные напряжения в |
|
|
|
|
|
|
|
поперечных сечениях для точек вблизи контура направлены по касательной к нему. Для этого положим, что в некоторой точке А касательное напряжение η направлено под углом, тогда его
можно разложить по направлениям касательной |
Т и нормали n к контуру сечения (7.12, а). По |
|||||||
|
|
|
б) |
|
|
|
|
|
закону парности касательных напряжений на поверхности стержня должно возникнуть напряжение |
||||||||
|
|
n |
, но эта поверхность свободна от нагрузки, |
следовательно, |
n |
0 , |
T |
направлено по |
n |
|
|
|
|
|
|||
касательной к контуру.
64
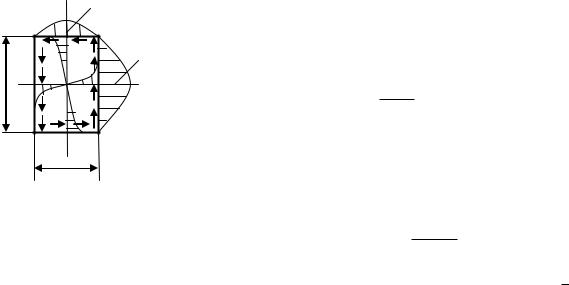
|
Аналогично можно показать, что в сечении с внешними углами напряжения равны нулю. |
|||||||||||||
Разложим напряжения вблизи угла на две составляющие 1 |
и 2 |
(7.12,б), так как парные им |
||||||||||||
напряжения и |
равны нулю, то и в ноль обращаются |
|
1 |
и |
2 |
. Значит, вблизи внешнего угла |
||||||||
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
||
касательные напряжения в поперечном сечении отсутствуют. |
|
|
|
|||||||||||
|
B |
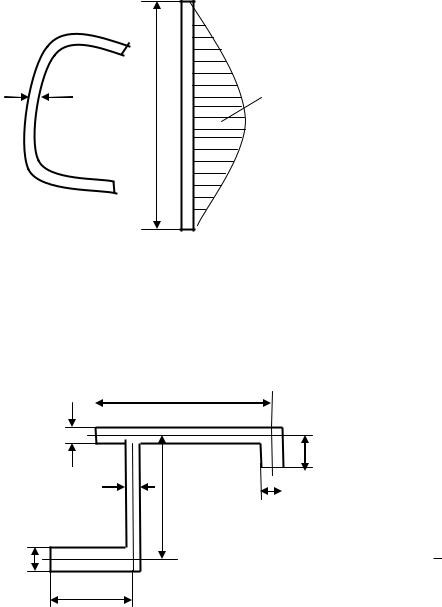
На рис. 7.13 |
показана эпюра касательных напряжений для |
|||||||||||
|
бруса прямоугольного сечения, полученная методами теории |
|||||||||||||
|
|
|
||||||||||||
|
|
|
упругости. Как видим, в углах напряжения равны нулю, а |
|||||||||||
|
B |
А m ax |
наибольшей величины они достигают в точках А по средине |
|||||||||||
|
|
|||||||||||||
|
A |
|
больших сторон: |
|
|
|
|
|
|
|
|
|
||
h |
A |
|
|
|
|
|
|
M k |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
А |
m ax |
, |
|
(7.15) |
||||||||
|
|
|
|
|
|
hb2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
B |
|
в точках В касательные напряжения вычисляются по формуле: |
|||||||||||
|
Рис.7.13 |
В m ax . |
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Здесь h – размер большой стороны, |
b – размер меньшей |
|||||||||||
|
|
|
||||||||||||
|
|
|
стороны прямоугольника. |
|
|
|
|
|||||||
Коэффициенты α, β и η зависят от отношения сторон h/b. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
М к |
|
|
|
Угол закручивания находится из выражения |
|
|
|
G hb3 . |
(7.16) |
||||||||
Коэффициент |
так же является функцией отношения сторон. При h/b≥10 1 , 0,742 . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица |
h/b |
1 |
1,5 |
1,75 |
2 |
2,5 |
3 |
4 |
6 |
8 |
10 |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
α |
0,208 |
0,231 |
0,239 |
0,246 |
0,258 |
0,267 |
0,282 |
0,299 |
0,307 |
0,313 |
0,333 |
|
|
|
|
|
|
|
|
|
|
|
|
β |
0,141 |
0,196 |
0,214 |
0,229 |
0,249 |
0,263 |
0,281 |
0,299 |
0,307 |
0,313 |
0,333 |
|
|
|
|
|
|
|
|
|
|
|
|
η |
1, 00 |
0,859 |
0,82 |
0,795 |
0,766 |
0,753 |
0,745 |
0,743 |
0,742 |
0,742 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Для формул (7.15), |
(7.16) введем геометрические параметры: |
||||||||||
|
|
W hb2 |
, I |
k |
hb3 |
, |
|||||
|
|
|
k |
|
|
|
|
||||
тогда они примут вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
m ax |
|
M k |
, |
M k |
. |
|
|||
|
|
||||||||||
|
|
|
|||||||||
|
|
|
Wk |
|
|
|
GI k |
|
|||
|
|
|
|
|
|
|
|
||||
7.2.5 Свободное кручение тонкостенных стержней открытого профиля
Характерной геометрической особенностью тонкостенных стержней является то, что их толщина существенно меньше прочих линейных размеров. Они разделяются на замкнутые и открытые.
Характер распределения напряжений в поперечном сечении тонкостенного стержня проще всего устанавливается при помощи плѐночной аналогии.
Рассмотрим расчѐтные формулы для открытого профиля (рис.7.14). На основе плѐночной аналогии было установлено, что напряжения в стержне сильно не изменятся, ели профиль сечения распрямить. Из этого следует, что напряжения в криволинейном открытом профиле будут примерно такими же, как и в прямом. Следовательно, в этом случае можно использовать расчѐтные формулы
65
|
m ax для прямоугольного сечения с большим отношением |
|||||||||
|
s |
h |
10 |
1 |
|
|||||
|
сторон. При отношении |
, тогда получим |
||||||||
|
b |
3 |
||||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
3M k |
, |
|
(7.17) |
|
|
|
|
m ax |
|
|
|
||||
|
|
|
|
|
2 s |
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
|
3М к |
|
(7.18) |
||||
|
|
|
|
. |
|
|||||
|
|
|
G 3 s |
|
||||||
Здесь S -длина контура поперечного сечения (бòльшая сторона прямоугольника);-толщина профиля ( меньшая сторона прямоугольника).
Полученные расчѐтные формулы являются общими и не зависят от формы профиля, если он может быть развѐрнут в прямоугольник.
7.2.6 Свободное кручение составного открытого профиля
|
|
s3 |
|
Если тонкостенный открытый профиль |
|
|
|
||
|
|
|
является составным (рис. 7.15), то поступают |
|
3 |
|
|
|
|
|
|
|
следующим образом: крутящий момент в сечении |
|
|
|
|
|
|
|
|
|
s4 |
рассматривают как сумму моментов, действующих |
|
|
|
||
|
2 |
|
на отдельных участках; угол поворота i отдельных |
|
|
4 |
|
||
|
|
участков равен углу поворота всего сечения, |
||
|
s |
|
||
|
2 |
|
т.е., i . В этом случае согласно формулам (7.17 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
), (7.18) |
|
|
n |
1 |
n |
|
1 |
Ik Iki |
i3si , |
|
|
i 1 |
3 i 1 |
||
|
|
|||
|
s1 |
Рис.7.15 |
|
|
|
3M k |
|
|
. |
(7.19) |
|
G( 3s 3 |
... 3s |
n |
) |
|||
|
1 1 2 |
n |
|
|
|
|
При помощи плѐночной аналогии установлено, что максимальные касательные напря-жения возникают на участке с максимальной толщиной m ax . Для этого участка, которому пропишем номер i, также справедливы формулы (7.18), (7.19):
|
|
|
|
|
|
|
3M ki |
; |
3M ki |
|
, |
|
||||||||
|
i |
max |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
2 s |
|
|
G 3 s |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
i |
i |
|
||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
i |
|
|||||
где M k |
- доля крутящего момента, соответствующего i- ому участку; |
|||||||||||||||||||
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
единое для всех участков. Исключая из этих выражений M k |
, находим |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
i |
|
m ax |
|
G m ax |
, |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
учитывая выражение (7.20), получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
m ax |
|
|
|
|
|
|
3M k m ax |
|
|
|
|
|
|
|
|||||
|
|
( 3 s |
3 |
... 3 s |
n |
) |
|
|
|
|
||||||||||
|
|
|
|
|
|
1 1 |
|
2 |
|
|
n |
|
|
|
|
|
|
|||
- угловое перемеще-ние,
(7.20)
7.2.7 Кручение тонкостенного стержня с замкнутым профилем
Рассмотрим кручение стержня с поперечным сечением в форме тонкостенного замкнутого профиля (рис.7.16). В этом стержне, в отличие от открытого профиля, напряжения по толщине
66
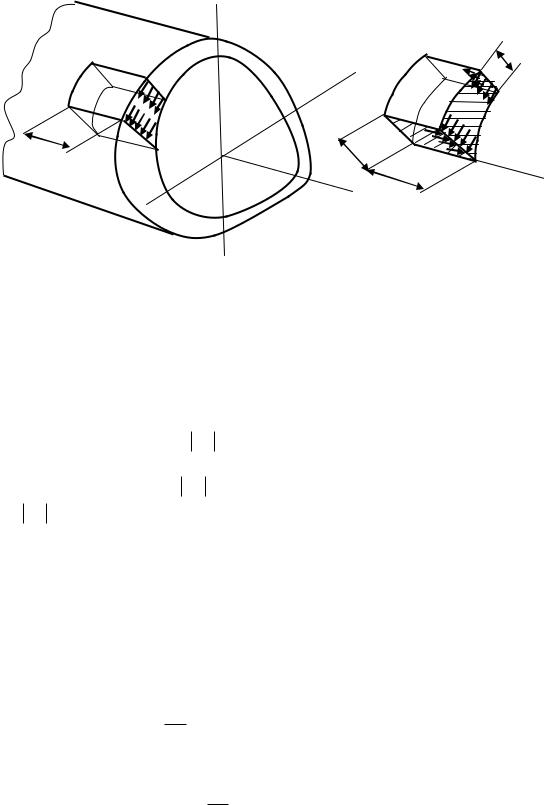
стенки распределяютя равномерно. Выделим из этого стержня элементарный объѐм длиной dz, расстояние между точками 1 и 2 которого произвольное. Пусть толщина контура в точке 1 будет δ1, а в точке 2 – δ2. Обозначим соответственно через η1 и η2 напряжения в поперечном сечении. В
продольных сечениях будут действовать парные напряжения 1/ 1, 2/ 2 .
|
|
y |
|
|
|
2 |
x |
2/ |
δ2 |
|
2 |
|
||
|
|
|
||
1 |
η2 |
|
1 |
η2 |
|
|
|
|
|
dz |
|
δ2 |
|
η1 |
|
η1 |
/ |
||
|
|
dz |
z |
|
|
|
1 |
||
|
|
|
|
|
|
|
z |
|
|
|
|
Рис. 7.16 |
|
|
Составим для рассматриваемого элемента уравнение равновесия, спроектировав все силы на направление оси стержня
1 1dz 2 2dz .
Из полученного равенства следует, что ηδ = const, так как точки 1 и 2 взяты произвольно. Таким образом, произведение ηδ по длине замкнутого контура является величиной постоянной. На участках с меньшей толщиной напряжения будут соответственно бòльшими.
Выразим крутящий момент через напряжения η. Для этого возьмѐм на контуре элементарную дугу длиной ds (рис. 7.17). Момент силы η·δ·ds относительно произвольной точки О равен ηδds|ОА|. Тогда
Мк = ∫ ОА ds .
Так как ηδ по длине дуги не изменяется, то получим Мк = ηδ ∫ ОА ds .
Выражение ОАds представляет собой удвоенную площадь треугольника ОВС, а интеграл от этого
произведения по длине замкнутого контура даѐт удвоенную площадь, ограниченную средней линией
контура. Обозначим эту площадь через F*. Таким образом,
Мк = ηδ2F*.
Наибольшее напряжение
m ax |
M K |
. |
|
2F m in |
|||
|
|
Для определения углового перемещения θ рассмотрим соотношение потенциальной энергии , выраженной через напряжения η и выраженной через внешний момент М. Удельная потенциальная энергия при сдвиге определяется выражением
u 2 . 2G
Энергия, накопленная в элементарном объѐме с размерами ds, z, δ равна
dU = 2 dz ds .
2G
Это выражение необходимо проинтегрировать по длине стержня и по дуге замкнутого контура
67

|
|
2 |
2 2 |
|
ds |
||
U = |
|
ds |
|
|
|
. |
|
2G |
2G |
|
|||||
|
|
s |
|
|
s |
||
Последний интеграл зависит от закона изменения толщины по дуге контура и является геометрической характеристикой сечения. Учитывая, что
ηδ = |
М к |
|
M |
, |
|
2F |
2F |
||||
|
|
|
|||
Получим |
|
|
|
|
|
M 2 |
|
ds |
|
U = |
|
|
. |
|
8GF 2 |
|
|||
|
|
s |
||
Теперь эту же энергию найдѐм как работу внешнего момента М на угловом перемещении θ:
U= 12 М .
Из равенства этих двух выражений находим
М ds . 4GF 2 s
Если толщина δ по дуге контура не меняется, то
М s , 4GF 2
где s - длина замкнутого контура.
Для рассмотренного тонкостенного замкнутого профиля вводятся геометрические параметры Wk, Ik, которые согласно полученным формулам для вычислений напряжений углов поворотов определятся выражениями:
W k 2F min , Ik 4F 2 .ds
s
Теперь формулы для вычислений напряжений углов поворотов примут вид:
m ax М к , M k .
Wk GI k
Контрольные вопросы
1.Когда брус испытывает кручение?
2.Что называется валом?
3.Какие внутренние усилия действуют в поперечном сечении вала? Как они определяются?
4.Какие напряжения действуют в поперечном сечении вала?
5.Как определяются максимальные напряжения в поперечном сечении вала?
5.Условие прочности при кручении вала ?
6.Какие перемещения возникают в вале при кручении и как они определяются?
7.Как определяется жѐсткость при кручении вала?
68
8. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
8.1 Основные понятия
Под устойчивостью понимается способность конструкции сохранять свою первоначальную форму равновесия при воздействии внешних сил.
При эксплуатации конструкция может подвергаться воздействиям, которые стремятся еѐ вывести из равновесия. Эти воздействия называются возмущающими. Если после прекращения возмущающих воздействий конструкция возвращается в исходное состояние, то еѐ состояние называется устойчивым. Если конструкция не возвращается к исходной форме равновесия, то еѐ положение будет не устойчивым.
Под потерей устойчивости понимается переход от устойчивой формы равновесия к неустойчивой.
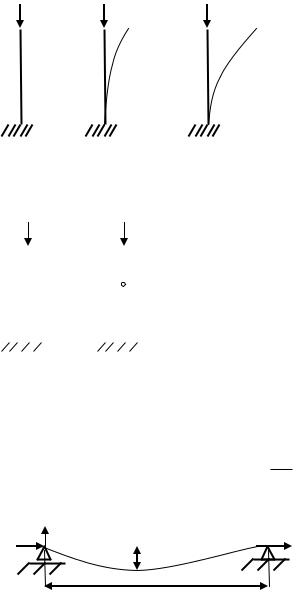
Рассмотрим достаточно длинный стержень по сравнению с размерами его поперечного сечения и нагрузим его силой F, которая будет постепенно возрастать.
|
|
F |
|
F=Fкр |
|
F≥Fкр |
Пока сила F мала стержень сохраняет прямолиней- |
||||||||||||
|
|
|
|
ную форму. С увеличением еѐ до некоторого значе- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ния F=Fкр после отклонения стержня он уже не вып- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рямляется. Положение стержня будет неустойчивым. |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При дальнейшем увеличении нагрузки, когда F>Fкр , |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
может произойти разрушение из-за потери устойчи- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Сила, превышение которой вызывает потерю устойчивости, называется критической и |
|||||||||||||||
обозначается Fкр, критические напряжения определятся формулой кр |
Fкр |
. |
|||||||||||||||||
Абрутто |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
F1 |
|
|
|
F2 |
Критические напряжения не зависят от местных ослаблений |
|||||||||||
|
|
|
|
|
|
поперечного сечения бруса. |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Допускаемое напряжение при потере устойчивости |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
кр |
, |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
у |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
nу |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
здесь n – коэффициент запаса по устойчивости |
|
||||||||
8.2 Формула Эйлера для критической силы
Вывод формулы Эйлера рассмотрим на примере двух опорной балки, нагруженной сжимающей осевой силой F. При F=Fкр балка прогнется. Запишем дифференциальное уравнение изогнутой оси:
EIy Fкр у , у Fкр y 0 .
ЕI
здесь I=Imin.
|
у |
|
|
|
Fкр |
k 2 |
|
|
Fкр |
|
|
z |
Обозначим |
|
, получим дифференциальное |
||
EI |
||||||||
|
|
у |
|
|
|
|||
|
|
уравнение второго порядка без правой части. |
||||||
|
|
ℓ |
||||||
|
|
|
|
|
|
|||
y k 2 y 0 (8.1).
Его решение имеет вид:
y Asin kz B coskz .
Значения А и В определятся из граничных условий (z = 0 и z=ℓ). В рассматриваемой балке имеем при z=0 y=0; при z=ℓ y=0. Тогда из (8.1) следует
69

Asin 0 B cos0 0,
так как cos0 0 , sinkℓ≠0, то В=0, тогда
Asinkℓ=0.
Но A≠0, так как балка не будет иметь прогибов, поэтому sinkℓ=0, т.е.kℓ=0, , 2π, 3π,…nπ.
Из последнего равенства находим
k2= n 2 2 = Fкр ,
2 EI
откуда следует формула
Fкр n2 2 EIm in ,
2
n≠0, тогда при n=1 получим окончательное выражение для критической силы, называемой формулой Эйлера:
F |
2 EI |
m in |
. |
(8.2) |
|
2 |
|||||
кр |
|
|
|
8.3 Влияние условий закрепления стержня на величину критической силы
Уравнение изогнутой оси стержня при потере устойчивости определится формулой
y Asin z ., т.е. она представляет собой дугу синусоиды. Для рассмотренного стержня, шарнирно
закрепленного по концам (эйлеровский случай), изогнутая ось принимает форму полуволны синусоиды длиной ℓ. Стержень с жестким закреплением при изгибе принимает форму четверти волны синусоиды, а полая полуволна будет располагаться на длине 2ℓ. Для такого стержня
критическая сила будет равна F |
2 EI |
min . |
|
||
кр |
(2 )2 |
|
|
||
Для сопоставления критической силы эйлеровского стержня с критической силой стержня, имеющего другие условия закрепления концов, вводится коэффициент приведения длины, который показывает во сколько раз следует изменить длину стержня с заданными условиями закрепления по сравнению с длиной стержня с с шарнирно закрепленными концами. Форма изогнутой оси и коэффициенты приведения еѐ длины представлены на
Fк  Fк
Fк
2ℓ
ℓ
Fк Fк
Fк
0,7ℓ 0,5ℓ
0,5ℓ 0,5ℓ
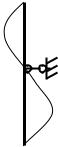
1 |
2 |
0, |
0, |
0, |
рисунке
70
