Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Самарский национальный исследовательский университет им. ак. С.П. Королёва (бывш. СГАУ, СамГУ)

Предмет:

Сопротивление материалов

Файл:

Сопромат Лекции Филатов

.pdf

Скачиваний:

Добавлен:

29.03.2016

Размер:

1.65 Mб

Скачать

☆

<<< < Предыдущая 12 / 82 3 4 5 6 7 8 > Следующая >>>

знак, следовательно, есть такое положение осей, в которых центробежный момент инерции равен нулю. Такие оси называются главными. Главные оси, проходящие через центр тяжести сечения,

называются главными центральными осями инерции сечения.

Моменты инерции относительно главных

центральных осей называются главными центральными

моментами инерции и обозначаются I x

, I y

dA2

, причем

Х2

dA1

I x0 > I y0 .

Х1

Если сечение имеет ось симметрии (ось y на рис.2.8), то

У2

У1

эта ось всегда будет главной осью инерции сечения.

Действительно, для любой элементарной площадки в

окрестности точки 1 в силу симметрии найдется такая же

площадка в окрестности точки 2. При этом А1=А2, у1=у2, х1= -

х2,, тогда I xy xydA x1y1dA х2 у2dA = x1 y1 dA

А2

	Рис. 2.8	+ x1 y1dA 0 .
	Рис. 2.8	А2
		А2

Таким образом, ось у является главной осью, так как центробежный момент инерции относительно еѐ равен нулю.

2.5 Зависимость между моментами инерции при повороте осей

Пусть задана система координат главных центральных осей x0,y0, для которой известны

моменты инерции I x

, I y

, центробежный момент инерции в

У0

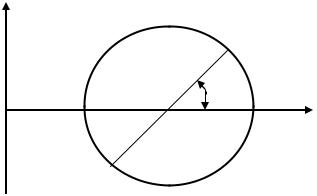
этих осях равен нулю (рис.2.9). Вычислим моменты инерции

этого сечения относительно новых осей x,y, повернутых по

отношению к главным на угол α - угол между осями x0 и x. Он

будет положительным, если поворот от оси x0 к оси x

происходит против часовой стрелки и отрицательным - если по

α v

часовой стрелке.

Из рис. 2.9 следует:

= х0

cos y0 sin ,

Х0

cos x0 sin

y = y0

С учетом этих формул запишем выражения для моментов

инерции рассматриваемого сечения в координатных осях x, y:

Iх = у 2 dА =

(у0 cоsα - х0 sinα)2 dA =

у 02 cоs2 α dA –

Рис.2.9

-2

х 0у0cоsα· sinα dA+

х02 sin 2α dA,

т.е.

cоs 2α - 2 Іх

у cоsα· sinα + I

sin 2α.

Іу = х2 dА = (х0csα + у0sinα)2 dA =

х 02 cоs 2α dA ++2 х 0

у0cоsα· sinα dA+

у 02 sin 2 α dA=

= I

cоs 2α + 2 Іх

cоsα ·sinα + I

sin 2α.

y 0

0 0

Іху= хуdA = (х0 cos y0 sin )(y0 cos x0 sin )dA =

АА

= x0 y0 cos2 dA x02 cos sin dA y20 sin cos dF y0 x0 sin2 dA =

А										A						A								A
= Ix	y	cos2 Iy							0	cos2α ·cоsα ·sinα + I x							0	cоsα∙ sinα - I x				0	y	sin2α.
0		0							0								0					0		0
Так как			I				0	,		cоsα ∙sinα =				sin 2		, то окончательно получим
Так как			I	x		y	0	,		cоsα ∙sinα =						, то окончательно получим
				x	0	y	0							2
										Ix	Ix		0	cos2 Iy						sin2 ,
													0							0
										Iy	Ix		0	sin2 Iy						cos2 ,
													0						0
										Ixy		Ix0 I y0			sin 2 .
										Ixy					sin 2 .
														2
Складывая выражения Іх и Іу, получим
												I x I y I x						0		I y	.
																		0			0

Таким образом, при повороте координатных осей сумма осевых моментов инерции не изменяется.

2.6 Графический способ исследования моментов инерции. Круги Мора

Можно показать, что формулы для моментов инерции

І = I

cоs

α +

sin

α , І =

cоs

α + I

sin

α., І =

I x0

I y0

sin2α представляют

ху

уравнение окружности в параметрической форме. Поэтому вычисление моментов инерции по полученным аналитическим формулам можно заменить графическим определением этих величин в системе координат (Іх, Іу), Іху, построив круг, называемый кругом инерции.

В графическом способе исследования моментов инерции рассматриваются прямая и обратная задачи.

Прямая задача: известны главные центральные моменты инерции I x0 , I y0 , требуется

графическим способом найти моменты инерции Іх, Іу, Іху относительно осей х и у, повернутых от главных осей на угол α.

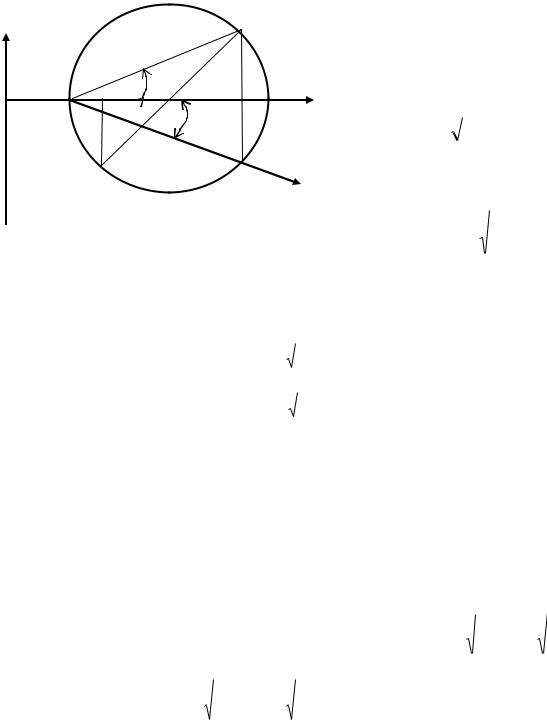
В координатной системе (Іх, Іу) , Іху (рис.2.10) построим круг на диаметре АВ, отложив в масштабе отрезки ОА= I x0 , ОВ = I y0 . В центре круга С от оси абсцисс отложим центральный угол

2α (α >0, если он откладывается против часовой стрелки), пересечение стороны этого угла с окружностью обозначим через Dх, а диаметрально ей расположенную точку через Dу. Проекции этих точек на ось абсцисс обозначим через Кх,, Ку.

Докажем, что отрезки ОКх= Іх, ОКу= Іу, КхDх= Іху .

Из рис.2.10 видно, что ОКх=ОС + СКх, ОКу=ОС – СКу, ОС=ОВ+ВС,

ВС=АС=СDх=

I x

I y

, тогда

Iху

Dх

ОС= I

у 0 +

I x

I y

I x

I y

Ку

2α

CКх= СDхcos2α =

I x

I y

∙cos2α,

Кх

I ,I

I x

I y

х у

ОКх=

∙cos2α =

Рис.2.10

I х0

(1 cos 2 )

у0

(1 cos 2 ) .

Так как 1+cos2α =2 cos2α, 1-cos2α =2sin2α., то

ОК	х	=	I	x0	∙ cos2α +			I		y0	∙sin2α = І ,
	х			x0						y0	х
ОК	у	=	I	x0	∙ sin2α + I				y0		∙cos2α = І ,
	у			x0					y0		у
						I x	I y	0
DхКх = СDх ∙sin2α =							0	0	∙sin2α = Іху
DхКх = СDх ∙sin2α =							2		∙sin2α = Іху
							2

Обратная задача: известны моменты инерции относительно центральных осей

Іх, Іу, Іху, необходимо определить главные центральные моменты инерции I x0 , I y0 и положение

главных центральных осей.

Отложим в масштабе по координатным осям (Іх, Іу), Іху отрезки ОКх= Іх, ОКу= Іу,

КхDх = Іху, КуDу = - Іху (рис.2.11). На отрезке DХDУ как на диаметре построим круг и обозначим на

оси абсцисс его крайние точки : крайнюю правую

Іху

Dх

точкой А, крайнюю левую то Из преды-дущей

задачи следует: ОА= I x

, ОВ= I y

. Найдем

значения этих величин, выразив их через отрезки

Ку

Кх

круга: ОА=ОС+СА,

ОВ=ОС-ВС,

α0

СА=ВС=СDХ= (CК х )

(К х Dх )

Dу

Х0

СКх = СКу=

I х I у

Dх

тогда

Рис.2.11

(I x I y )2

)2 ,

СА=ВС=

ху

ОС = ОКу + СКу = Іу +

I у

I х

I у

Используя значения полученных отрезков, запишем выражения для главных центральных моментов инерции

ОА= I x Im ax I

4(I

ОВ=

I y Im in I

4(I

Из рис. 2.11 следует, что α0 = -α, тогда

tgα0 =

K x Dx!

I xy

2.7 Радиусы и эллипс инерции

Осевые моменты инерции сечения можно представить как произведение площади сечения на

квадрат некоторой величины, называемой радиусом инерции: Іх = y 2 dA = =А х2

, где х - радиус

I у

инерции относительно оси х. Из этого выражения следует, что i

, i

. Главным

центральным осям будут соответствовать главные радиусы инерции

Ix0

I y0

	2		2
Выражение х20		у20		=1 представляет уравнение эллипса, полуосями которого являются
iy	0	ix	0
	0		0
главные радиусы инерции.
У0		Х0
				У0	Х0
			правильно		неправильно
				Рис. 2.12
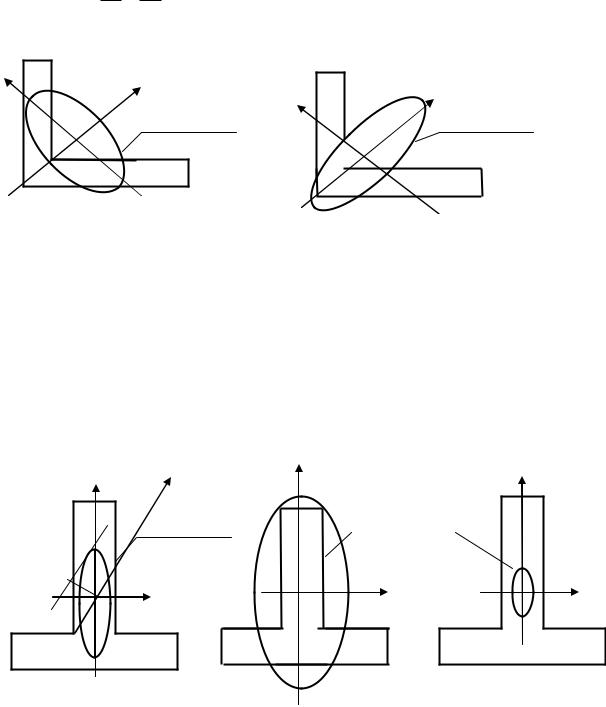
Эллипс, построенный на полуосях, равных главным радиусам инерции, называется эллипсом
инерции.
Необходимо отметить, что при построении эллипса отрезки, равные ix						, откладываются по
						0
оси у0, а отрезки, равные iy				, - по оси х0. Поэтому эллипс инерции всегда вытянут вдоль сечения
				0
(рис.2.12), и он не может быть больше сечения, а так же заметно меньше его (рис.2.13).
Для определения момента инерции относительно произвольной оси Х необходимо провести
касательную α -α к эллипсу инерции, параллельную этой оси. Перпендикуляр СК, опущенный из
центра эллипса С на эту касательную будет равен радиусу инерции, т.е., іх=СК, Iх=(СК)2А

У0	Х	У0	У0
	Х

	α	правильно	неправильно
			неправильно

к		Х0	Х0	Х0
α	с	Х0
α	с

Рис.2.13

3.7 Моменты инерции сложных сечений

При проверке прочности элементов конструкций приходится встречаться с поперечными сечениями довольно сложной формы, для которых нельзя вычислить моменты инерции таким простым путем, каким пользовались для треугольника, прямоугольника или круга. В этом случае сложное сечение разбивают на простые фигуры, для которых известны площади, координаты центров тяжестей и моменты инерции относительно собственных центральных осей (I xi , I yi ) . По

формулам (3.1) находят координаты центра тяжести c всего сечения в произвольно выбранных осях x0,y0, параллельных центральным осям хi , уi выделенных элементов. Через центр тяжести c проводят центральные оси сечения u, v, относительно которых вычисляют осевые и центробежный моменты

A1 A2

инерции по формулам (3.15). Моменты инерции относительно главных центральных осей определяются по формулам (3.20), а положение главных центральных осей – по формуле (3.18).

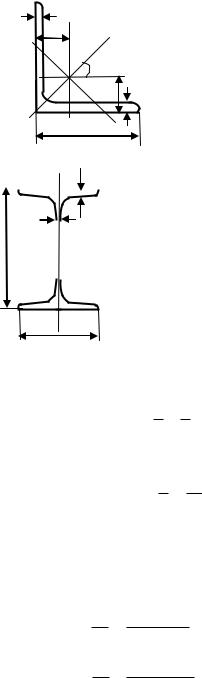
Пример. Для заданного сложного поперечного сечения, состоящего из двутавра №18 и уголка 100х100х12, вычислить значения главных центральных моментов инерции u , v и положение главных центральных осей u , v.

Решение 1. Размеры и геометрические характеристики элементов заданного сечения

Из справочных данных выпишем необходимые для расчетов размеры и геометрические характеристики элементов заданного сечения.

S
Z	у	х0
0
		a0=45º
		х
		S
	в	у0
	в

Уголок 100х100х12:

в=10 см, s =1,2 см, z0 =2,91 см, А= 22,6 см2, Iх = Iу =209

см2, I x0 =331 см2, I y0 =86,9 см2.

Для дальнейших расчетов необходимо знать величину центробежного момента уголка. Его вычислим по

формуле Ixy	Ix	0	I y	0	331 86?9	= -122,4 см4

	sin 2a				sin( 90 )

	y	t	Двутавр №18:
		t	h =18 см, в = 9 см, s =0,5 см, t =0,81 см, А = 23,4 см2, Iх =1290 см4,
	s
			Iу = 82,6 см4.
			Iу = 82,6 см4.
h		x	Оси х, у двутавра являются главными центральными осями (как оси
h			симметрии), поэтому центробежный момент инерции двутавра равен нулю,

			т.е. Iху = 0.

2. Определение центра тяжести сечения

bВычертим указанное сечение в масштабе и покажем на нѐм центры тяжестей элементов сечения c1 , c2 и их центральные оси (рис.2.14). Проведем

произвольные оси u,v, параллельные центральным осям элементов и определим в этих осях координаты центров тяжестей c1 и c2 :

uc1 2в 92 4,5 см,

uc2 вдвут вугол z0 =9+10-2,91=16,09 см,

h 18

vc1 2 2 см,

vc2 h z0 =18 - 2,91 = 15,09 см.

Учитывая, что геометрические характеристики сложного сечения находятся как сумма геометрических характеристик элементов, составляющих данное сечение, то координаты центра тяжести сечения вычислим по формулам

vc Su A

uc Sv A

Su(1) Su(2)

A1 A2

Sv(1) Sv(2)

A1vc		A2vc	2		23,4 9 22,8 15,09			12		см,
1			2
	A1 A2					23,4 22,8
	A1 A2					23,4 22,8
	A1uc A2uc			2		23,4 4,5 22,8 16,09			10.2		см.
		1		2
	A1 A2					23,4	22,8
	A1 A2					23,4	22,8

3. Вычисление моментов инерции относительно центральных осей X,Y

По найденным координатам отметим на чертеже сечения его центр тяжести с, проведѐм через него центральные оси х,у, параллельные центральным осям элементов, и вычислим относительно их моменты инерции, используя формулы преобразования моментов инерции при параллельном переносе осей, одни из которых центральные:

I (1)

I (2)

I (1)

A a2

I (2) A

;

I (1)

I (2)

I (1)

A в2

I (2)

в2

;

I (1)

I (2)

I (1)

A a

I (2)

xy xу

xу

x y

x у

Здесь: a1, в1 –расстояния между центральной осью сечения х центральными осями элементов сечения х1 и х2;

a2, в2 - – расстояния между центральной осью сечения у и центральными осями элементов сечения у1 и у2.

У1

У2

У0

С 2

α2

i у

α1

i у

VС

С1

VС

U C1

U С

Рис. 2.14

U С 2

Из чертежа 2.14 следует: a1

9 12 3см,

a2 vc2

15,09 12 3,09 см,

4,5 10,2 5,7 см,

16,09 10,2 5,89 см.

Осевые моменты инерции первого элемента (двутавра) относительно собственных

центральных осей x1,y1: I x(1)

1290cм4 , I y(1)

82,.6cм4 , I x(1)y

Осевые моменты инерции второго элемента (уголка) относительно собственных центральных

осей х2,у2: Ix(2)	Iy(2)	209cм4 , Ix(2)y	122,4см4 .
2	2	2	2

С учетом записанных формул и значений моментов инерции относительно собственных центральных осей получим:

Iх=1290+23,4*(-3)2+209+22,8*(3,09)2=1927,3 см4,

I y =82,6+23,4*(-5,7)2+209=22,8*(5,89)2=1804,9 см4,

Iху=0+23,4*(-3)*(-5,7)-122,4+22,8*3,09*5,89=692,7 см4.

4.Определение главных центральных моментов инерции и положения главных центральных осей

Главные центральные моменты инерции аналитическим способом вычислим по формуле

				(I			x	I	y	)	(I		x	I	y	)2	4 I 2
I m ax,m in							x		y				x		y		xy
																		=
														2				=
														2

	(1927,3 1802,9)											(1927,3 1802,9)2 4 692,72								3730,2 1390,97
=																					,
=														2						2	,
														2						2
Imax Iх						3730,2 1390,97									2560,6 см4,
Imax Iх															2560,6 см4,
			0							2
			0
Im in I y					3730,2 1390,97										1169,6 см4
Im in I y															1169,6 см4
			0							2
			0
Положение главных центральных осей определим по формуле
tg	0	I xy								692 ,7							0,914 , , 0		42,44
tg	0																0,914 , , 0		42,44
		Ix	Im in					1927 ,3 1169 ,6

Отложив угол α0 = - 42,40 по часовой стрелке от центральной оси Х, получим направление главной центральной оси х0, перпендикулярно ей проведем главную центральную ось у0.

Контрольные вопросы

1.Что относится к геометрическим характеристикам поперечного сечения бруса, используемых в сопротивлении материалов?

2.Как определяются статические моменты площади поперечного сечения бруса?

3.Как определяются статические моменты площади поперечного сечения бруса, если известны площадь и координаты еѐ центра тяжести ?

4.Как определяются осевые моменты инерции поперечного сечения бруса?

5.Формулы осевых моментов инерции прямоугольника?

6.Формулы осевых моментов инерции круга?

7.Формулы осевых моментов инерции кольца.

8.Как определяется полярный момент инерции поперечногоi сечения бруса?

у0

9.Как определяется центробежный момент инерции поперечного бруса?

10.Что называется моментом сопротивления сечения изгибу?

11.Формулы моментов сопротивления сечения изгибу прямоугольника, круга, кольца?

12.Что называется полярным моментом сопротивления сечения?

13.Формулы полярных моментов сопротивления круглого и кольцевого сечений.

14.Какие оси называются центральными?

15.Чему равны статические моменты площади сечения относительно центральных осей?

16.Какие оси называются главными?

17.Какие оси называются главными центральными?

18.Формулы преобразования моментов инерции при параллельном переносе осей?

19.Формулы преобразования моментов инерции при повороте от главных центральных осей?

20.Формулы для вычисления главных центральных моментов инерции?

21.Формула для определения положения главных центральных осей?

22.Порядок вычисления геометрических характеристик сложных сечений?

3. ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ И СЖАТИЕ

Прямой брус испытывает деформацию центрального растяжения, сжатия, если силы или их равнодействующая действуют вдоль его оси. В этом случае в поперечном сечении бруса из шести внутренних силовых факторов отличным от нуля будет один - нормальная сила N, которая определяется методом сечений.

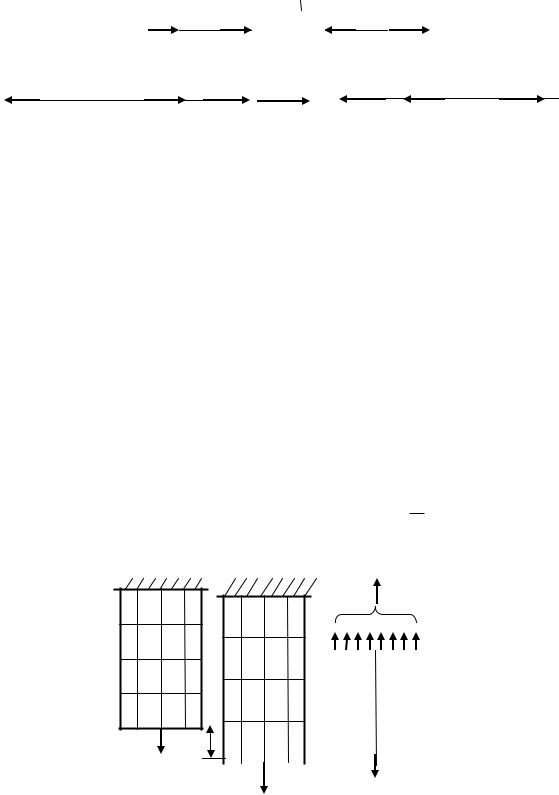
Рассечем брус (рис.3.1) на две части и рассмотрим равновесие каждой из них, составив сумму проекций всех сил, расположенных по одну сторону от сечения, на ось Z :

F1	F2	F3		F4
			F4


F1	F2	Z		F3	F4
F1	F2	Z			F4
		Nлев	Nправ

Рис.3.1

∑Ζлев=0, -F1 +F2 +Nлев = 0, Nлев = F1 -F2 , ∑Ζправ=0, - F3 +F4 -Nправ = 0, Nправ = - F4 +F3.

Нормальная сила Ν принимается положительной (Ν>0), если она направлена от сечения, и отрицательной (Ν<0), если она направлена к сечению.

3.1 Напряжения при центральном растяжении, сжатии

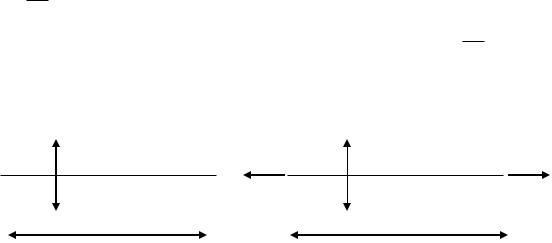
Задача определения напряжений является статически неопределимой задачей, т.к. неизвестен закон распределения внутренних усилий по площади сечения. Опыт показывает, что при центральном растяжении, сжатии строго выполняется гипотеза плоских сечений: поперечные сечения бруса плоские и перпендикулярные к оси (рис. 3.2, а) до деформации остаются плоскими и перпендикулярными к оси после деформации (рис. 3.2, б). Такая картина деформаций позволяет считать, что в поперечных сечениях бруса действуют только нормальные напряжения, равномерно

распределенные по сечению (ζ = const), а касательные напряжения равны нулю. В этом случае нормальная сила N (рис.3.2, в) является равнодействующей нормальных напряжений в поперечном

сечении: N= dA . Так как ζ = const , то N=ζA, откуда следует формула для нормальных

напряжений при центральном растяжении или сжатии: NA , здесь А – площадь поперечного

сечения бруса.

При растяжении ζ > 0, при сжатии ζ < 0, т.е., знак напряжений определяется знаком N.


F	∆ℓ
а)			F	в)
		б)
		б)
		F		Z

Рис.3.2

В продольных сечениях (параллельных оси бруса) напряжения отсутствуют. На наклонных площадках действуют и нормальные и касательные напряжения.

3.2 Продольные и поперечные деформации при центральном растяжении, сжатии

При растяжении брус удлиняется, а его поперечные размеры уменьшаются. Разность между длиной бруса после деформации ℓ1 и до деформации ℓ0 (рис.3.3) ∆ℓ = ℓ1- ℓ0 называется абсолютным удлинением. ∆ℓ>0 при растяжении и ∆ℓ<0 при сжатии. Экспериментально было установлено, что ∆ℓ

= ЕАF . Эта зависимость называется законом Гука в деформациях. Здесь: А – площадь поперечного

сечения бруса, ЕА - жесткость бруса при растяжении, сжатии, Е[ мН2 ] – упругая характеристика

материала, называемая модулем упругости при растяжении. Его значения для некоторых материалов приведены в таблице

	b0		F	b1		F

				ℓ1
	ℓ0			ℓ1
	ℓ0
			Рис.3.3
			Рис.3.3

	материал	сталь	медь	алюминий	титан	дерево

	Е, МПа	2∙105	1,1∙105	0,7∙105	1,2∙105	0,1∙105
Отношение ∆ℓ к первоначальной длине ℓ0				называется относительной продольной деформа-

цией, т.е. . Разделим левую и правую части выражения закона Гука на первоначальную

	0
длину ℓ0:		F	,	т.к. ,	F	, то ζ = Еε – это выражение называется законом Гука в
длину ℓ0:			,	т.к. ,		, то ζ = Еε – это выражение называется законом Гука в
	0	ЕА		0	А

напряжениях, из которого следует, что нормальные напряжения прямо пропорциональны относительному удлинению.

Абсолютная поперечная деформация бруса ∆b = b0 – b1 - это разность между поперечными

размерами до и после нагружения:. Отношение поп b называется относительной поперечной b0

деформацией. Между продольными и поперечными деформациями экспериментально установлена зависимость εпоп = -μεпрод, называемая законом Пуассона. Здесь εпрод - относительная продольная деформация, μ – коэффициент Пуассона, который так же является упругой характеристикой материала. Для металлов величина μ находится в пределах 0,25 -0,33. Наименьшее значение имеет пробка (μ=0), наибольшее – каучук(0,47).

3.3 Испытание на растяжение. Основные механические характеристики материала

Испытания материалов проводятся при растяжении вплоть до разрушения на стандартных образцах.

Образцы используются как круглые, так и плоские при соотношении размеров, определяемых

<<< < Предыдущая 12 / 82 3 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете Сопротивление материалов

#
29.03.2016516.82 Кб29Расчетно-проектировочные работы по сопротивлению материалов.pdf
#
16.03.2015613.54 Кб41СБОРНИК РАСЧЕТНО-ПРОЕКТИРОВОЧНЫХ РАБОТ ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ.pdf
#
29.03.2016152.26 Кб29СОПРОМАТ 2-ая 561.docx
#
16.03.2015342.37 Кб33СОПРОМАТ 1 РГР Вариант 548.docx
#
16.03.2015147.46 Кб37Сопромат 2ргр Вариант 309.doc
#
29.03.20161.65 Mб20Сопромат Лекции Филатов.pdf
#
16.03.20151.95 Mб31Сопромат Лекции Часть 1.pdf
#
29.03.2016517 Кб18Сопромат Расчетно-проектировочные работы.pdf
#
29.03.20161.34 Mб22Справочные данные. Часть 1.pdf
#
16.03.20151.48 Mб46СПРАВОЧНЫЕ ДАННЫЕ.doc