
Сопромат Лекции Филатов
.pdf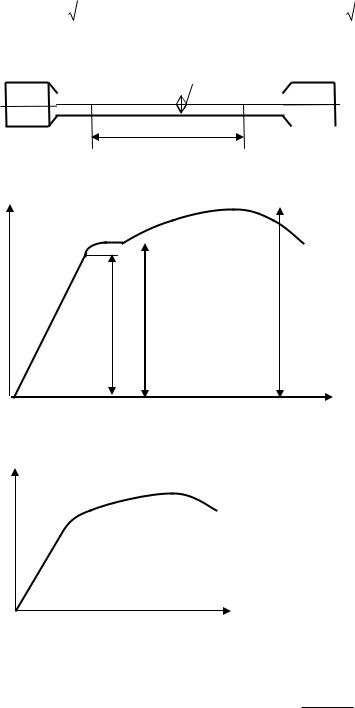
ГОСТом: |
|
0 |
|
11,3 - для нормальных образцов и |
|
0 |
|
5,65 |
- для укороченных ( 0 , А0 - длина |
||
|
|
|
|
|
|
|
|
||||
|
А0 |
|
|
А0 |
|||||||
|
|
|
|
|
|
|
|
||||
рабочей части и площадь поперечного сечения образца до испытаний, рис.3.4) . Результатом испытаний является диаграмма растяжения, устанавливающая зависимость
|
|
|
|
|
d0 |
|
|
|
|
|
|
|
|
между нагрузкой F и вызванной ею удлинением |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ℓ. Эта зависимость называется диаграммой рас- |
|
|
|
∙ |
|
|
|
|
|
∙ |
|
|
|
|
|
||
|
|
|
|
ℓ0 |
|
|
|
|
|
тяжения. Как правило, испытательные машины |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
оборудованы устройствами для автоматической |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
записи таких диаграмм. На рис.3.5 представлена |
|
|
|
|
|
Рис.3.4 |
|
|
|
|
|
|
|
|
. диаграмма растяжения малоуглеродистой стали. |
||
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим еѐ характерные участки. Участок |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ОА называется участком упругости, здесь вы- |
|
|
|
|
|
|
|
|
D |
||||||||
F |
|
|
С |
|
|
полняется закон Гука. После точки А линейная |
|||||||||
|
В |
|
|
|
|
|
Е |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
зависимость между усилием и деформацией |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
нарушается, но до точки В деформации остают- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ся упругими. На участке ВС деформации растут |
|
|
|
|
|
Fт |
|
|
Fмах |
|
без существенного изменения нагрузки, он |
||||||
|
|
Fпц |
|
|
|
|
|
|
|
|
|
называется участком текучести. Наличие пло- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щадки текучести ВС для металлов не является |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
характерным. В большинстве случаев при испы- |
|
0 |
|
|
|
|
|
|
|
|
|
|
∆ℓ |
|
тании на растяжение площадка текучести не об- |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
наруживается, и диаграмма растяжения образ- |
||
|
|
|
|
Рис.3.5 |
|
|
|
|
|
|
|
|
ца имеет вид кривой, показанной на рис.3.6. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
На участке СD у материала вновь появляется способность сопротивляться нагрузкам. Этот |
|||||||||||||||
F |
|
|
|
|
|
|
|
участок называется участком упрочнения. |
|||||||
|
|
|
|
D |
|
|
|
|
|
При приближении к точке D на образце зарождается |
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
шейка и после этого все деформации происходят в окрест-ности |
|||||||
|
|
|
|
|
|
E |
|
этой шейки вплоть до разрушения в точке Е. Падение нагрузки |
|||||||
|
А |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
F на участке DE объясняется уменьшением площади |
|||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
поперечного сечения образца. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
По результатам измерения размеров образца до и после |
||||
0 |
|
|
|
|
|
|
|
разрушения определяются характеристики пластичности: |
|||||||
|
|
|
|
|
|
остаточное относительное удлинение |
|||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
Рис.3.6 |
|
|
|
|
к |
0 |
100% |
|||||
|
|
|
|
|
|
|
|
|
|
||||||
0
иостаточное относительное сужение в месте разрыва
ΨА0 Ак 100%.
Ао
Здесь ℓ0, А0 соответственно длина рабочей части и площадь поперечного сечения образца перед испытанием,ℓк, Ак длина рабочей части и площадь наименьшего сечения разорванного образца.
Диаграмма растяжения в координатах F- ∆ℓ не отражает свойств материала, а является по существу характеристикой образца из данного материала, так как значения усилия F и удлинения ∆ℓ зависит от размеров образца. Чтобы исключить влияние размеров образца, диаграмму растяжения
перестраивают в диаграмму напряжений в координатах ζ – ε (рис.3.7).
21

Так как при подсчѐте ζ= |
F |
и ε= используются только первоначальная площадь А0 и |
|
|
|||
|
А |
|
0 |
|
0 |
|
|
первоначальная длина ℓ0 , то полученная таким путѐм диаграмма называется диаграммой условных напряжений. Она по характеру не отличается от диаграммы растяжения в координатах F- ∆ℓ.
ζ |
|
D |
|
Под механическими характеристиками |
||||
В |
|
|
понимаются значения напряжений и деформа- |
|||||
|
С |
|
ций, соответствующих определѐнным точкам |
|||||
|
|
|
||||||
|
А |
|
Е |
на диаграмме условных напряжений. |
||||
|
|
|
|
Пределом пропорциональности |
||||
|
|
ζу ζт |
ζв |
называется наибольшее напряжение, до |
||||
|
ζпц |
которого выполняется закон Гука (ζпц= |
Fпц |
). |
||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
А0 |
|
|
|
|
|
Пределом упругости называется |
||||
|
|
|
|
наибольшее напряжение, до которого |
||||
О |
|
|
ε |
деформации материала носит упругий |
||||
|
|
Рис. 3.7 |
|
характер (ζ = |
Fу |
). |
||
|
|
|
|
у |
||||
|
|
|
|
|
А0 |
|||
Пределом текучести (физическим) называется напряжение, при котором деформации растут
без заметного увеличения нагрузки (ζт= F ).
А0
Для материалов, не имеющих площадки текучести определяется условный предел
текучести ζ0,2 – это напряжение, при котором остаточные деформации составляют 0,2% первоначальной длины.
Пределом прочности, или временным сопротивлением называется максимальное
напряжение, которое материал выдерживает без разрушения (ζв= Fмах ).
А0
Основные механические характеристики материалов, применяемых в технике, приводятся в справочной литературе.
3. 4 Явление наклѐпа
Если образец нагрузить до напряжений, больших предела упругости, но меньше предела прочности, например, до точки К (рис.3.6), а затем начать разгружать, то разгрузка будет происходить по прямой КL, параллельной начальному участку нагружения ОА. После разгрузки деформация образца уменьшится, но полностью не исчезнет. Отрезок LМ определяет величину
ζ |
К |
|
упругой деформации εу, а отрезок ОL – величину остаточной |
|
|
(пластической) деформации (εост). Повторное нагружение |
|
|
|
N |
|
|
А |
образца пойдѐт cначала по линии разгрузки КL, а затем по |
|
|
|
||
|
|
кривой КN, которую имел бы этот образец без промежуточной |
|
|
|
|
|
|
|
|
разгрузки |
|
|
|
Следовательно, после промежуточной разгрузки у |
|
|
|
материала повышается предел пропорциональности |
|
|
|
(упругости), но уменьшается пластичность. |
εЯвление повышения упругих свойств материала в результате
предварительного пластического деформирования называется
наклѐпом или нагартовкой.
22
Наклѐп возникает при вытяжке, холодной прокатке металла, в процессе штамповки и т.д. Часто он играет положительную роль и применяется для повышения упругих свойств проволоки, канатов, упрочнения поверхностного слоя детали. В тех случаях, когда наклѐп вреден, его устраняют отжигом.
3.5 Расчѐт на прочность при центральном растяжении, сжатии
Наиболее распространѐнным методом расчѐта на прочность деталей машин и элементов конструкций является расчѐт по допускаемым напряжениям. Он заключается в вычислении максимального рабочего напряжения детали, которое не должно превышать предельного напря-
жения, свойственного данному материалу и условиям эксплуатации, т.е., |
мах |
L , где |
L |
- |
|
n |
|
||
|
|
|
|
предельное (опасное) напряжение материала детали, n >1 – коэффициент запаса, устанавливае-мый нормами прочности. Для пластических материалов ζL= ζт, для хрупких ζL=ζв
L |
|
Величину [ ] = n |
называют допускаемым напряжением. Условие прочности будет иметь |
вид: | ζ|наиб ≤ [ζ] или | ζ|наиб ≤ | N наибА | ≤ [ζ].
Из этого условию прочности следует три задачи сопротивления материалов:
1. Проверка прочности | N наиб | ≤ [ ];
А
2. Назначение размеров поперечного сечения А ≥ N наиб ;
3.Определение грузоподъѐмности N наиб ≤ ∙А
3.6Статически неопределимые задачи при центральном растяжении, сжатии
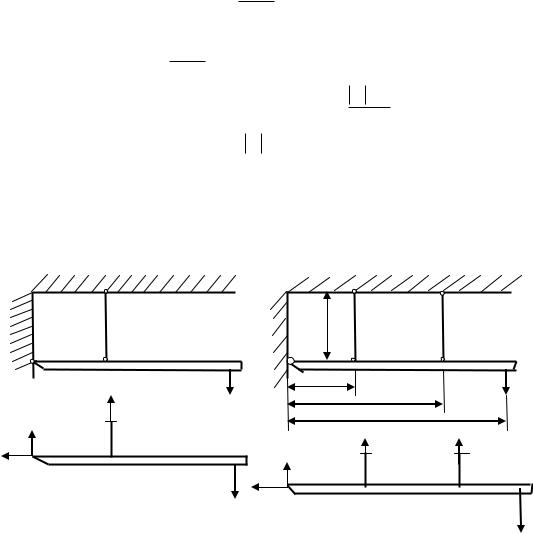
Кстатически неопределимым относятся конструкции, в которых число неизвестных усилий превышает количество уравнений равновесия. На рис.3.7 представлена статически опреде-
|
ℓ |
1 |
2 |
|
|
||
0 |
|
|
|
F |
b |
с |
F |
|
|||
N |
|
|
|
|
|
|
|
V |
|
N1 |
N2 |
|
|
||
H |
V |
|
|
F |
Н |
|
|
α) |
|
b) |
|
|
|
||
|
|
|
|
статически определимая система |
статически неопределимая система |
||
Рис.3.7
23
лимая система: она имеет три неизвестных реакции и три уравнения статики. На рис.3.7 b изображена система, у которой четыре неизвестных усилия N1, N2, H ,V, а уравнений равновесия у неѐ также три, следовательно, эта система будет один раз статически неопределимой.
Для определения внутренних усилий N1, N2 воспользуемся уравнением равновесия
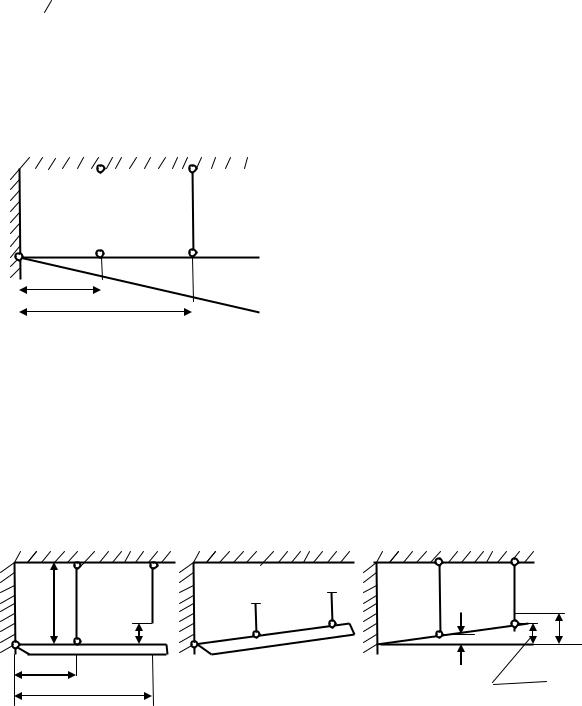
∑М0 =0, N1∙ b+ N2∙ с - F∙α=0 (3.1). Дополнительное уравнение можно получить, рассмотрев перемещения совместно деформируемых стержней (уравнение совместности деформаций). Считая горизонтальный стержень абсолютно жестким (недеформируемым), получим (рис.3.8)
|
|
1 |
|
|
b |
, так как |
|
|
= |
N1 1 |
, |
|
= |
|
N 21 2 |
, то |
N1 Е2 А2 |
|
= |
b |
. Выразим из этого уравнения усилие |
||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
c |
|
|
|
|
|
1 |
|
Е1 А1 |
|
2 |
|
|
|
|
Е2 А2 |
|
|
Е1 А1 N 2 |
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
первого стержня N1 = |
E1 A1b |
|
N 2 и подставим его значение в уравнение равновесия (3.1). |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
E2 |
A2 c |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
E1 A1b |
|
N 2 b + N2 c = F α, откуда следует N2 |
|
|
|
Fa |
|
|
|
|
, N1 |
|
Fa |
|
|
. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
E A c |
|
|
b2 E A |
|
c2 E |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
2 A2 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c cE A |
|
|
|
|
bE1 A1 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из полученных значений N1 и N2 следует, что |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
статическая неопределимость конструкций может быть |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
раскрыта, если известны жесткости еѐ элементов. Так как с |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
увеличением жесткости первого элемента Е1А1 усилие N1 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
возрастает, а N2 |
|
уменьшается и наоборот, то в статически |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
неопределимых конструкциях полного использования |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
∆ℓ1 |
|
|
|
|
|
|
|
|
|
|
прочностных свойств материала невозможно. |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ℓ2 |
|
|
|
|
|
Рассмотрим случай, когда элементы конструкции |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выполнены из одного материала, т.е., Е1=Е2=Е, |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ζ]1=[ζ]2=[ζ], а также примем, что площади стержней и их |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.3.8 |
|
|
|
|
|
|
|
|
|
|
|
длины одинаковы. А1=А2=А, ℓ1 =ℓ2 |
=ℓ, тогда N1 |
|
|
|
Fab |
, |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
c2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
N |
|
|
|
Fac |
, |
N 2 |
2 2 |
|
: 1 |
|
c |
. Из последнего соотношения следует, |
что ζ > ζ в |
c |
|
раз, |
|
|||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
c |
2 b2 |
|
N1 |
|
1 |
Е Е b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
b |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
поэтому ζнаиб =ζ2 =[ζ], ζ1 < [ζ].
3.7 Монтажные напряжения в статически неопределимых системах
Пусть при сборке стержневой конструкции (рис.3.9 а) стержень 2 оказывается на величину δ корче необходимой длины ℓ. После монтажа стержень 1 окажется сжатым, стержень 2 – растянутым. Для определения внутренних усилий (рис.3.9 б), возникших в этих стержнях
ℓ 1 |
|
2 |
|
0 |
δ |
0 |
|
b |
|
б) |
|
а) |
c |
||
|
|||
|
|
N 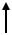 N
N
|
δ |
|
∆ℓ1 |
в) |
δ-∆ℓ2 |
Рис.3.9 |
|
после сборки, запишем уравнение равновесия: ∑М0 = -N1b+N2c = 0 (3.2). Из этого уравнения видно, что задача статически неопределимая. Для составления недостающего второго уравнения рассмотрим соотношение деформаций стержней после монтажа (рис. 3.9 в)
24

|
|
|
|
|
N1 |
|
|
|
|
|
|
1 |
|
b |
или |
|
E1 A1 |
|
|
b |
(3.3) |
||
2 |
c |
|
N2 |
|
c |
||||||
|
|
|
|
E2 A2 |
|
|
|
|
|||
Совместное решение уравнений (3.2) и (3.3) позволяет определить усилия N1 и N2
N1 |
|
|
b |
|
|
, |
N2 |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
( |
c |
|
b2 |
) |
( |
c2 |
|
|
b |
) |
|||
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|||||||
|
|
E1 A1 |
|
cE2 A2 |
|
|
|
|
bE1 A1 |
E2 A2 |
|
||
Температурные напряжения
При нагревании бруса его длина изменится на величину ∆ℓТ= αℓ∆Т. Здесь α – температурный коэффициент линейного расширения материала, ℓ - длина бруса до нагревания, ∆Т- величина изменения температуры.
Рассмотрим задачу определения температурных напряжений в брусе, жестко закреп-
|
Z |
|
|
|
|
|
RВ |
|
|
|
|
|
RА |
|
|
|
|
|
|
t |
|
α∆Т=- |
N |
|
=- |
||
|
||||||
|
EA |
E |
||||
лѐнном по торцам. Из условия равновесия ∑Z= RА+ RВ=0 видно, что рассматриваемая задача является статически неопределимой. Из условий закрепления следует: ∆ℓ=∆ℓТ+∆ℓN=0.
Здесь ℓТ=αℓ∆Т, ∆ℓN= EAN , тогда αℓ∆Т+ ENA =0, , ζt=-Е α∆Т.
Контрольные вопросы
1.Когда брус испытывает деформацию центрального растяжения, сжатия?
2.Какие внутренние усилия возникают при ц.р.с.?
3.Какие напряжения возникают при ц.р.с.? Как они определяются?
4.Что такое абсолютная деформация? Относительная деформация?
5.Как сформулировать закон Гука в деформациях? Закон Гука в напряжениях?
6.Как сформулировать закон Пуассона?
7.Что такое предел пропорциональности? Предел упругости? Предел текучести (физический)? Предел текучести условный? Предел прочности?
8.Условие прочности при ц.р.с.?
9.Как определяется жѐсткость при ц.р.с.?
10.Что называется допускаемым напряжением и как оно определяется?
11.Какие системы называются статически неопределимыми?
12.Какие уравнения используются при раскрытии статической неопределимости?
25
4.Основы теории напряженного и деформированного состояния
4.1Основные понятия.
На различно ориентированных площадках, проходящих через одну и ту же точку, будут отличаться и по величине и по направлению.
Совокупность напряжений по всем площадкам, проходящим через данную точку, называется
.напряженным состоянием в точке тела Исследуя напряженное состояние тела в некоторой точке А, в ее окрестности выделяют
элемент в виде бесконечно малого параллелепипеда с ребрами dx, dy, dz.
y |
y |
|
Py


 A
A
Px
|
x |
|
|
|
A |
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
dx |
|
|
|
Рис. 4.1 |
z |
||
|
|
|
|
|
|
dy
dz
Pz
Так как все грани параллелепипеда бесконечно малы и в пределе проходят через точку А, то напряжения на соответствующих секущих плоскостях – это напряжения в исследуемой точке. Такой подход возможен на основании гипотезы сплошной среды.
Обозначим полные напряжения, действующие на гранях параллелепипеда Px, Py, Pz (рис. 4.1). Здесь индексы показывают нормаль к площадке, на которой действует напряжение. Эти полные напряжения раскладываются на три составляющие в направлении координатных осей: одно по нормали к площадке и два в ее плоскости (рис. 4. 2).
y |
|
|
|
Индекс нормального напряжения соответствует |
|||||
|
|
|
оси, перпендикулярно которой расположена площадка. |
||||||
|
y |
|
|||||||
|
|
Первый индекс касательного напряжения обозначает |
|||||||
|
|
|
|
||||||
|
|
|
|
нормаль к площадке , на которой оно действует, второй |
|||||
yz |
|
yx |
|
соответствует оси, параллельно которой направлено это |
|||||
|
|
напряжение. |
|
|
|
|
|||
|
|
xy |
|
|
|
|
|
||
zy |
|
x |
Нормальные растягивающие напряжения прини- |
||||||
|
|
маются |
положительными, |
нормальные сжимающие – |
|||||
|
zx |
xz |
|
отрицательными. |
|
|
|
|
|
|
|
Касательные |
напряжения |
|
считаются |
||||
A |
|
|
|
||||||
|
|
|
|
||||||
|
|
x положительными, |
если |
нормаль |
к |
площадке |
|||
|
|
|
|||||||
z |
|
|
|
поворачивается до совмещения с вектором напряжения |
|||||
|
|
|
|
по часовой стрелке (рис. 4.3). |
|
|
|||
z |
Рис. 4.2 |
|
26

n |
|
n |
η>0 |
|
η<0 |
|
|
|
|
|
|
Рис. 4.3
Согласно методу сечения, выделенный элемент под действием рассматриваемых напряжений будет находиться в равновесии. Вследствие достаточно малой длины ребер элемента напряжения на параллельных гранях можно считать равными, но противоположно направленными. Поэтому напряженное состояние в точке может быть задано девятью компонентами по трем взаимно перпендикулярным площадкам
x xy xz
yx y yz
zx zy z
4.2Закон парности касательных напряжений. Главные площадки,
главные напряжения.
Касательные напряжения связаны между собой определенной зависимостью, которая следует
из условий равновесия параллелепипеда |
(рис. 4.2): M x 0, |
My 0, M z 0. Рассмотри |
||
первое уравнение равновесия: M x |
0, |
yz dx dz dy zy |
dx dy dz 0 . |
Из него следует |
yz zy . Аналогично из уравнений |
My 0, M z 0 получим xz zx , |
xy yx . Таким |
||
образом xy yx , yz zy , xz zx .
Эти соотношения носят название закона парности касательных напряжений: касательные напряжения по двум взаимно перпендикулярным площадкам равны по абсолютной величине и противоположны по знаку, т.е. касательные напряжения на двух взаимно перпендикулярных площадках направлены либо к линии пересечения этих площадок, либо от нее.
Таким образом, на гранях выделенного элемента имеем не девять, а только шесть независимых компонентов напряжений: x, y, z, xy, yz, zx.
|
|
|
|
При изменении ориентации граней выделенного параллелепипеда |
|||
|
|
ζ2 |
меняются и напряжения, действующие на его гранях. При этом, как |
||||
|
|
|
доказывается в теории упругости, можно провести такие три взаимно |
||||
ζ1 |
перпендикулярных площадки, на которых касательные напряжения будут |
||||||
отсутствовать. |
|
|
|||||
ζ3 |
|
Площадки, на которых нет касательных |
напряжений, |
||||
|
|
|
|
||||
называются главными, а нормальные напряжения на этих площадках |
|||||||
|
|
|
|||||
|
|
|
– главными напряжениями (рис 4.4). |
|
|
||
Рис.4.4 |
|
|
|
Главные напряжения обозначаются 1, 2, |
3, при расстановке |
||
|
|
||||||
индексов следует выполнять соотношение 1 2 3.
Это неравенство следует понимать в алгебраическом смысле. Пусть одно из главных напряжений равно нулю, другое растягивающее – 40 МПа, третье сжимающее – 140 МПа, тогда
1 40 МПа , 2 0 , 3 140 МПа .
4.3Виды напряженного состояния.
Врасчетах на прочность деталей машин и элементов конструкций необходимо знать в
каждой точке напряженное состояние, которое вполне может быть определено |
значениями |
трех главных напряжений в этой точке. В отдельных случаях одно или два |
главных напряжения |
27
могут равняться нулю. Соответственно различают три вида напряженного состояния в точке: объемное, плоское и линейное.
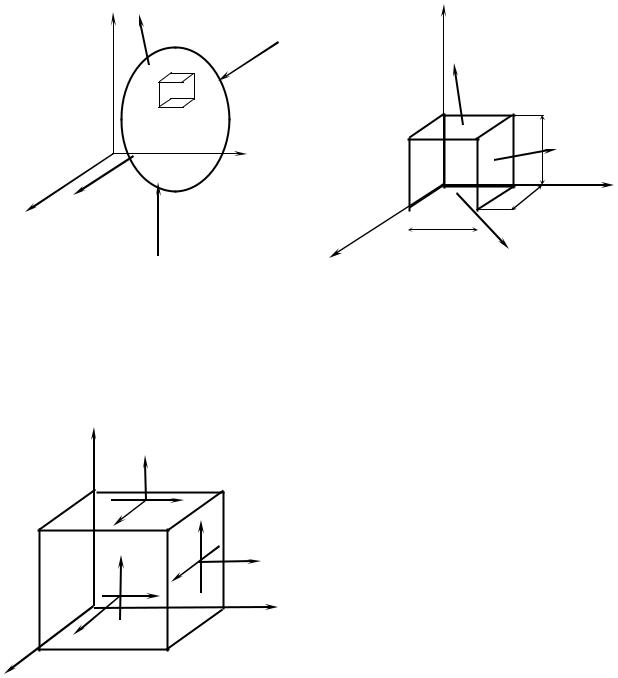
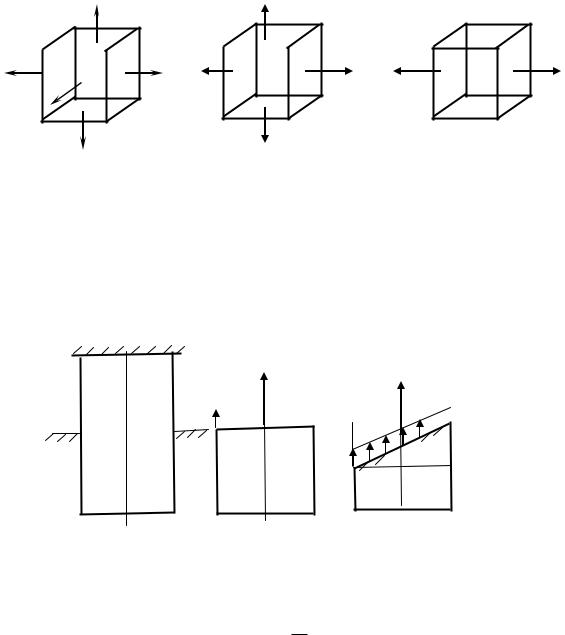
Напряженное состояние называется объемным или трехосным, если все три главных напряжения отличны от нуля (рис. 4.5, а). Такое напряженное состояние возникает, например, в зоне контакта зубьев шестерни или шарика и кольца подшипника.
Напряженное состояние называется плоским или двухосным, когда одно из трех главных напряжений равно нулю (рис. 4.5, б). Этот вид напряженного состояния наиболее часто встречается в расчетах на прочность. Такое напряженное состояние возникает при кручении круглых валов, в брусе, работающем на изгиб и т.д.
2 |
2 |
|
||
|
1 |
|
1 |
1 |
|
|
|||
|
||||
|
|
|
||
3
а) |
б) |
в) |
Рис. 4.5
Напряженное состояние называется линейным или одноосным, если два из трех главных напряжений равны нулю (рис. 4.5, в)
4.4 Линейное (одноосное) напряженное состояние.
Примером линейного напряженного состояния может служить напряженное состояние в брусе при растяжении – сжатии.
Рассмотрим брус, нагруженный силой F (рис. 4.6), тогда в плоскости перпендикулярной его
N  N
N
 ζ
ζ  pα
pα

 α
α
 F
F  F
F  F
F
Рис. 4.6
оси
N F , NA FA .
Рассмотрим площадку, наклоненную под углом к поперечному сечению. 0, если он отсчитывается против часовой стрелки. Обозначим полное напряжение на этой площадке р . Для его определения применим метод сечений. Отбросим верхнюю часть и рассмотрим в равновесии нижнюю часть.
28

β = 900 + α
N р |
|
|
A |
F , |
р |
F |
cos cos |
|
|||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
cos |
|
|
A |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
n |
|
|
Проекцией этого напряжения: |
на нормаль к площадке n |
||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
α |
|
|
|
будет нормальное напряжение ζα , на саму площадку - |
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
касательное напряжение (рис 4.7). |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P cos cos2 |
(4.1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
sin cos sin |
sin 2 (4.2) |
||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
Определим напряжение на площадке, перпендикулярной к |
|||
|
|
|
|
|
|
|
|
|
рассмотренной. В этом случае угол между вектором р и |
||||||
|
|
|
Рис.4.7 |
|
|||||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
90 , тогда |
|
|||||||||
|
|
cos2 90 sin 2 , |
|
|
(4.3) |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2 90 sin 2 . |
(4.4) |
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Из выражений (4.1) - (4.3) следует: |
|
|
||||||
|
|
|
|
|
|
- сумма нормальных напряжений на двух взаимно перпендикулярных |
||||
|
|
|
|
|
|
|
|
|
||
площадках есть величина постоянная; а максимальные касательные напряжения действуют на
|
m ax 450 |
|
|
|
площадках, повернутых от главных на угол 45: |
2 |
. (4.5) |
||
|
|
|
|
4.5Плоское (двухосное) напряженное состояние.
Пусть по боковым граням элементарного параллелепипеда действуют главные напряжения 1 и 2. Определим напряжения на произвольной наклонной площадке, расположенной под углом к главной (рис. 4. 8).
n
β=-(90-α)
2
ζβ
n
|
|
|
|
|
|
|
|
Напряжения и , |
действующие на площадке , |
|
|
||||||||||
|
|
|
|
|
|
|
вызываются действием как напряжения 1, так и напряжения |
|
|
||||||||||||
|
|
|
|
1 |
|
|
2. Применяя принцип суперпозиции, получим выражения |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
>0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
α |
|
|
|
|
, |
, |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
- напряжения, вызванные действием 1, |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
где , |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
- напряжения, вызванные действием 2. |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
, |
|
|
|
|||||||||||
|
|
|
ηα |
|
|
2 |
Согласно уравнениям (4.1), (4.2) |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
cos |
2 |
, |
|
|
1 |
sin 2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ηβ |
|
|
|
|
|
|
|
|
|
и |
|
следует учесть, что нормаль n |
|
|
|||||
|
|
|
|
|
|
Для определения |
|
|
|
||||||||||||
|
|
|
|
|
|
|
образует с направлением 2 |
угол = |
|
90 – . Согласно |
|
|
|||||||||
|
|
|
|
|
|
|
правилам знаков для углов, он будет отрицательным. Тогда |
|
|
||||||||||||
|
|
|
|
1 |
|
|
sin 2 sin 2 90 |
sin 180 2 |
sin 2 |
|
|
||||||||||
|
|
|
Рис. 4.8 |
|
|
cos2 cos2 90 cos2 90 cos2 90 sin 2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
90 2 sin |
|
|
С |
|
учетом |
этих |
|
преобразований |
|
|
|
2 cos |
2 |
2 |
, |
|||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
2 |
sin 2 |
2 |
sin 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
29
Тогда |
|
|
cos2 |
|
2 |
sin 2 |
|
(4.6) |
|
|
|
1 |
|
|
|
|
|||
|
|
|
1 2 |
sin 2 |
|
(4.7) |
|||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Напряжения на площадке, перпендикулярной к рассмотренной, найдем по формулам (4.3), (4.4) учитывая, что угол между напряжением ζ1 и нормалью nβ равен 90 , а между напряжением ζ2 и этой же нормалью – α.
|
|
|
sin 2 |
2 |
cos2 |
|
(4.8) |
|
|
1 |
|
|
|
|
|||
|
|
1 2 sin 2 |
|
(4.9) |
||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При сложении выражений (4.6) и (4.8) подтверждается положение, что сумма нормальных напряжений на взаимно перпендикулярных площадках – величина постоянная,
т. е. 1 2 const .
Для определения наибольшего и наименьшего значения нормального напряжения вычислим первую производную от по выражения (4.6) и приравняем ее к нулю:
d |
2cos sin |
2sin cos |
2 |
|
|
2 |
sin 2 0 . |
(4.10) |
|
||||||||
d |
1 |
|
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Уравнение (4.10) |
удовлетворяется при =0 и =90. Согласно (4.6) |
max 1 при |
|||||
=0, а при =90 min 2 . В обоих этих случаях =0, следовательно, нормальные
напряжения 1 и 2 принимают экстремальные значения на главных площадках.
Наибольшее значение касательных напряжений, как следует из формулы (4.7), будут при =
45, т.е.,: m ax |
|
0 |
|
1 |
2 |
(4.11) |
45 |
|
|
2 |
|||
|
|
|
|
|
||
|
|
|
|
|
|
4.6Графический метод исследования напряженного состояния в точке.
Построение кругов Мора
Можно оказать, что уравнения |
|
|
|
1 |
cos2 |
|
2 |
sin 2 |
, |
|
|
1 2 |
sin 2 |
|
|
|
|
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
представляют уравнение окружности в параметрической форме. Поэтому для графического метода исследования напряженного состояния используются круги напряжений, называемые кругами Мора
.
В теории напряженного состояния можно разграничить две основные задачи:
Прямая задача: в точке известны положение главных площадок и соответствующие им главные напряжения, требуется определить нормальные и касательные напряжения по площадкам, наклоненным к главным под углом .
Обратная задача: в точке известны нормальные и касательные напряжения, действующие по двум взаимно перпендикулярным площадкам, проходящим через данную точку, требуется определить главные напряжения и положение главных площадок.
Рассмотрим решение этих задач графическим методом
4.6.1Прямая задача
Аналитическое решение прямой задачи определяется формулами (4.6) – (4.9). Для графического решения строится на плоскости в координатах круг Мора
(рис. 4.9) в следующей последовательности.
30
