
Сопромат Лекции Филатов
.pdf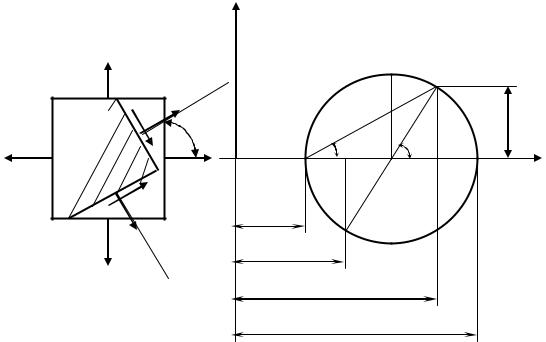
|
|
|
η |
|
|
|
|
|
|
|
|
Dс |
|
ζ2 |
|
nα |
|
|
|
Dα |
|
ζα |
|
|
|
|
ηα |
|
ηα |
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
B |
α |
2α |
A |
|
|
ζ1 |
|
Kβ |
|
ζ |
|
|
|
C |
Kα |
||
|
ηβ |
|
ζ2 |
|
|
|
|
|
|
|
|
|
|
|
ζβ |
|
ζβ |
|
|
|
ζ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nβ |
|
|
ζα |
|
|
Рис. 4.9 |
ζ1 |
Выбирается прямоугольная система координат так, чтобы ось абсцисс была параллельна большему из главных напряжений 1, по этой оси в выбранном масштабе откладывются отрезки ОА и ОВ, численно равные напряжениям 1 и 2, а на их разности (на отрезке АВ) как на диаметре проводим окружность с центром в точке С.
Из крайней левой точки (В) круга проводим луч, параллельный внешней нормали к рассматриваемой площадке, т.е. под углом к оси . Точка пересечения этого луча с окружностью (D ) имеет своими координатами отрезки D K и OK , численно равные касательному и нормальному напряжениям, действующим на рассматриваемой площадке.
Из рис.4.9 следует: AC=BC=CDα= 1 |
2 |
, СКα=СКβ |
=СDαcos2α = 1 2 cos2α |
||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
D K |
|
CD sin 2 |
1 2 |
sin 2 |
|
|
|
|
|||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
OK |
|
OB BC CK |
|
|
|
|
1 2 |
|
1 |
2 |
cos2 |
||||
|
|
2 |
|
|
2 |
||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
1 2 1 cos2 2 |
1 cos2 2 cos2 |
|
|||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 cos2 2 sin 2
Точка D , лежащая на противоположном конце диаметра от точки D , характеризует напряжения β и , действующие по наклонной площадке, перпендикулярной к первой.
D |
|
K |
|
D K |
|
1 |
2 sin 2 |
|
|
|
|
|
2 |
||||
|
|
|
|
|
|
|
|
OK |
|
OB BC CK |
|
|
2 |
1 2 1 |
2 cos 2 |
|||
|
|
|
|
|
|
2 |
2 |
|||
|
|
|
|
|
|
|
|
|
||
|
1 |
sin 2 |
2 |
cos2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
Выполненные преобразования проведены с учетом, что 1+cos2α = 2cos2α., 1-cos2α = 2sin2α. |
||||||||||
Полученные выражения для , , ηα |
и |
ηβ полностью |
совпадают с аналитическими |
|||||||
формулами (4.6) - (4.9). |
|
|
|
|
|
|
|
|
|
|
31
В заключение следует отметить, что каждая точка круга Мора имеет своими координатами напряжения, действующие на соответствующей площадке, следовательно, зная главные напряжения для плоского напряженного состояния, можно с помощью круга Мора определить напряжения, действующие на различных площадках, проходящих через данную точку. Максимальное
касательное напряжение соответствует точке Dc и равно радиусу круга CD |
max |
1 2 . |
c |
2 |
|
|
|
4.6.2Обратная задача.
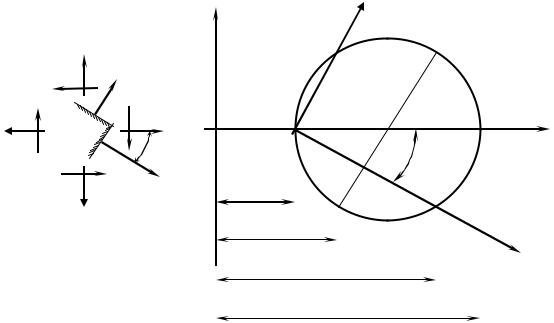
Довольно часто приходится решать обратную задачу, т. е. по напряжениям на произвольных площадках , , , определять величину и направление главных напряжений. Проще эта задача решается графически, т. е. с помощью круга Мора (рис. 4.10). Рассмотрим порядок его построения.
Прямоугольную систему координат , выберем так, чтобы ось абсцисс была параллельна большему из нормальных напряжений (пусть ). На оси отложим в выбранном масштабе отрезки ОК , ОК , численно равные и . Из точек К и К проведем перпендикуляры К D , К D ,
которые численно равны соответственно и ηβ на диаметре, построим круг с центром в точке С. Крайнюю правую точку пересечения круга с осью
обозначим буквой А, крайнюю левую – буквой В. Касательные напряжения в этих точках равны нулю, следовательно, ОА= 1, ОВ= 2 – главные напряжения (.в соответствии с прямой задачей).
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
D |
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
B K |
C |
|
K A |
|
||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
D |
|
D |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.10
параллельна большему из нормальных напряжений (пусть ). На оси отложим в выбранном масштабе отрезки ОК , ОК , численно равные и . Из точек К и К проведем перпендикуляры
К D , К D , которые численно равны соответственно и ηβ (К D = , К D = ηβ = ). На отрезке D D , как на диаметре, построим круг с центром в точке С. Крайнюю правую точку
пересечения круга с осью обозначим буквой А, крайнюю левую – буквой В. Касательные
напряжения в этих точках равны нулю, следовательно, ОА= 1, ОВ= 2 – главные напряжения (.в соответствии с прямой задачей).
32

Из |
рис.6.10 |
|
определим |
|
|
|
радиус |
|
|
|
круга |
|
R |
|
|
и |
|
величину |
отрезка ОС |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
СК |
|
2 К |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 4 |
2 |
|
|
|||||||||||||||||
R CD АС ВС |
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
(4.12) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ОС ОК |
К С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.13) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
C учетом выражений (4.12) , (4.13) получим следующие формулы для главных напряжений |
||||||||||||||||||||||||||||||||||||||||||
ОА= ζI = ОС + R = |
|
|
+ |
|
|
2 4 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.14) |
||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ОВ = ζII |
= ОС – R = |
|
|
- |
|
|
|
|
2 |
4 2 |
|
|
|
|
|
|
|
|
|
(4.15) |
||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Или |
I ,II |
2 |
2 4 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.16) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для определения направления главного напряжения 1 проведем луч через крайнюю левую точку круга В и точку D , которая симметрична точке D относительно оси . Направление луча ВD совпадает с направлением 1, направление 2 перпендикулярно ему. Угол 0 определится из треугольника ВК D (рис. 6.10):
|
|
|
|
|
|
|
tg 0 |
|
K D |
|
(4.17) |
||
BK |
II |
|||||
|
|
|
|
Угол 0 |
считается положительным, если его откладывают от оси против часовой стрелки. |
||||||||
4.7 |
Напряжения на произвольной площадке при объемном напряженном |
||||||||
|
|
|
|
состоянии |
|
|
|
|
|
|
|
|
|
|
|
В элементарном параллелепипеде, по |
|||
|
|
|
|
|
граням которого действуют все три главных |
||||
|
|
3 |
|
2 |
напряжения, рассмотрим произвольную |
||||
|
|
|
площадку , нормаль к которой составляет с |
||||||
|
|
3 |
|
|
|||||
|
|
|
n |
координатными осями 1,2,3 углы α1 α2 α3.(рис. |
|||||
|
|
|
|
||||||
|
|
|
|
|
4. 11). На этой площадке будет действовать |
||||
|
|
|
|
|
|
|
|
|
|
|
|
р |
|
|
полное напряжение рα, составляющее с |
||||
|
|
|
|
||||||
|
|
|
|
1 |
нормалью n угол α. Определим его проекции |
||||
|
|
|
|
на нормаль к площадке - ζα и на саму |
|||||
|
|
|
|
1 |
|||||
|
|
|
|
|
площадку – ηα. |
|
|
|
|
|
|
|
|
1 |
|
Нормальное напряжение, исполь-зуя |
|||
2 |
|
|
|
принцип суперпозиции, можно пред-ставить |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Рис.4.11 |
|
|
выражением |
= 1 |
2 |
3 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
- напряжение на рассматриваемой |
|||
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
площадке, вызванное действием 1 , а |
||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
2 , 3 - соответственно от напряжений |
||||
|
|
|
|
|
2 и 3 .Для вычисления этих величин |
||||
33

воспользуемся формулой для линейного напряжѐнного состояния: 1 = 1 cos2 1 ,
|
|
|
|
|
|
|
|
|
|
|
2 = 2 cos2 |
2 , 3 |
= 3 cos2 3 . |
|
|
|
|
|
|
|
|
С учетом этих значений нормальные напряжения на произвольной площадке определятся |
||||||||||
равенством |
|
|
|
|
|
|
|
|
|
|
|
|
1 cos2 1 2 cos2 2 3 cos2 3 |
|
|
|
(4.18 ) |
||||
Для вывода формулы |
касательных напряжений |
ηα |
следует |
рассмотреть его векторную |
||||||
|
|
|
|
|
|
|
|
|
|
|
величину |
1 |
2 |
2 |
2 |
2 |
, то |
|
2 |
2 |
|
3 . Так как p |
|
p |
. |
|||||||
Опуская выводы, которые следуют из уравнений равновесия рассматриваемой трѐхгранной пирамиды (рис. 3.11), запишем формулу в окончательном виде для вектора полного напряжения на площадке nα :
р2 (1 cos1 )2 ( 2 cos2 )2 ( 3 cos3 )2 .
С учѐтом этого выражения
|
|
2 |
2 |
1 |
2 |
2 |
2 |
2 |
2 |
|
2 |
|
1 |
cos |
2 |
cos |
3 |
cos |
3 |
(4.19) |
В качестве примера рассмотрим напряжения на площадке, равнонаклонѐнной ко всем главным площадкам. Такая площадка называется октаэдрической, а напряжения, действующие на этой площадке, называются октаэдрическими.
Так как для такой площадки 1 2 3 , а учитывая, что всегда
|
|
|
|
|
|
|
|
cos2 |
1 |
cos2 |
2 |
cos2 |
3 |
1, то |
cos2 1 . |
Следовательно |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
окт |
1 2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.20) |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
окт |
|
1 |
12 |
22 32 |
|
1 |
1 2 |
|
3 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
3 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
1 |
|
|
2 |
2 |
|
2 |
|
1 |
|
2 |
2 |
2 2 |
|
2 |
|
2 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
2 |
3 |
|
|
2 |
3 |
3 |
|
|||||||||||||||||||||||||||||||||||||
|
3 |
|
|
|
1 |
|
|
|
|
9 |
|
1 |
|
|
2 |
|
|
3 |
|
|
|
|
|
1 |
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.21) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
2 |
3 |
2 |
3 |
2 |
2 |
|
2 |
2 |
2 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
3 |
1 |
|
|
|
2 |
|
|
|
3 |
|
1 |
|
|
2 |
|
|
2 |
3 |
|
|
1 |
3 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
|
2 2 |
|
2 |
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
3 |
|
|
|
1 |
|
|
2 |
|
|
3 |
1 |
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Так же, как и в случае плоского напряженного состояния, при объемном напряженном состоянии сумма нормальных напряжений по трем взаимно перпендикулярным площадкам, проходящим через рассматриваемую точку, есть величина постоянная.
4.7.1 Круг Мора для объемного напряженного состояния.
Рассмотрим графический метод анализа напряженного состояния в точке при объемном напряженном состоянии.
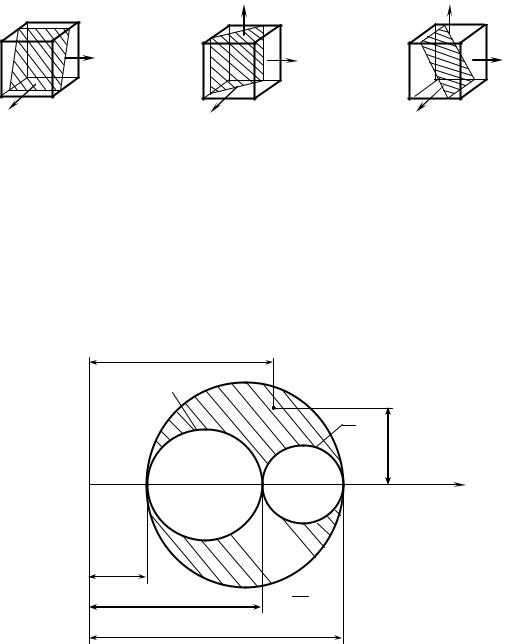
Прежде всего определим напряжения на площадках, параллельных одному из главных напряжений (рис. 4.12)
34
 2
2
1
3
а)
2 |
2 |
|
|
1 |
1 |
3 |
3 |
|
|
б) |
в) |
Рис.4.12 |
|
На площадках, параллельных 1, (рис. 4.12, а), напряжения зависят только от 2 и 3 и не зависят от 1, т. к. cos 1 cos 90 0 , тогда согласно (4.18)
|
|
|
|
|
2 |
cos2 |
|
2 |
|
3 |
cos2 |
3 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
D б
3  2
2 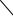 в
в
1
Рис. 4.13.
Круг Мора, соответствующий этому случаю, представлен на рис. 4.13 кругом «а». Напряжения в семействе площадок, параллельных 2 , определяются по кругу «б», а в
семействе площадок, параллельных 3 – с помощью круга «в».
В теории упругости доказывается, что площадкам общего положения соответствуют точки, лежащие в заштрихованной области (рис. 4.13).
Из представленного рисунка следует, что наименьшее и наибольшее нормальные напряжения
равны наименьшему и наибольшему главным напряжениям min 3 , m ax 1 . Наибольшие касательные напряжения равны радиусу наибольшего круга
max 1 3
2
и действуют по площадке, равнонаклонѐнной к площадкам максимального и минимального из главных напряжений ( 45 ).
35
4.7.2 Деформации при объемном напряженном состоянии.
Обобщенный закон Гука
Рассматривая вопросы прочности при объемном и плоском напряженных состояниях, необходимо в соответствии с основными гипотезами считать, что материал изотропный, следует закону Гука, а деформации малы.
Изучая центральное растяжение, сжатие, было установлено, что относительные продольная и поперечная деформации определяются выражениями
|
|
|
|
|
прод |
|
, |
|
поп |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.12) |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
Е |
|
|
|
|
|
|
Е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Эти равенства выражают закон Гука при простом растяжении или сжатии, т.е. при линейном |
||||||||||||||||||||||||||||||||||||||||||
напряженном состоянии (рис. 4.14). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Рассмотрим зависимость между напряжениями и деформациями в случае объемного |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
напряженного состояния. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Применяя принцип суперпозиции, объемное напряженное |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
состояние изобразим как сумму трех линейных напряженных состояний |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(рис. 4.15). В этом случае деформацию по направлению первого главного |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
напряжения 1 |
можно записать |
|
1 |
|
где |
|
, |
|
, |
|
|
- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
1 , |
|
1 |
1 |
|
1 |
|||||||||||||||||
Рис.4.14 |
|
|
|
|
|
|
относительные удлинения в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
направлении 1, вызванные соответственно действием только |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ζ1 |
|
|
|
|
|
ζ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
ζ3 |
|
|
|
ζ2 = |
|
|
+ |
|
|
|
ζ2+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
напряжениями 1, 2, 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Поскольку |
|
является для напряжения 1 |
продольной |
деформацией, а |
|
|
|
- |
||||||||||||||||||||||||||||||||||
|
1 |
|
|
1 , |
|
1 |
|
|||||||||||||||||||||||||||||||||||
поперечными деформациями, то из формул (4.12) следует: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
, |
|
2 , 3 . |
|
|
|
|
|
|
|
|
|
|
(4.13) |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
Е |
|
1 |
|
|
|
Е |
1 |
|
Е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Складывая эти величины, получим |
|
1 |
1 |
2 |
3 |
|
1 |
|
1 |
|
2 |
|
3 |
. |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Е |
|
Е |
Е |
|
Е |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Аналогично получаются выражения для двух других главных удлинений. В результате |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
1 |
|
1 |
|
|
|
1 |
|
2 |
|
3 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
Е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
1 |
|
|
2 |
|
3 |
|
1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
(4.14) |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
Е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3 |
|
|
1 |
|
3 |
|
1 |
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
Е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Эти формулы носят название обобщенного закона Гука для изотропного тела, т. е. определяют зависимость между линейными деформациями и главными напряжениями в общем случае объемного напряженного состояния. Из этих формул легко получить закон Гука для плоского
напряженного состояния. Например, 1 0 :
36
1 2 3 ,
Е
2 2 3 ,
Е
3 3 2 .
Е
Выражения (4.14) справедливы не только для главных деформаций, но и для относительных деформаций по любым трем взаимно перпендикулярным направлениям.
При выводе аналитического выражения обобщенного закона Гука в этом случае будем исходить из условия, что угловые деформации не зависят от нормальных напряжения, а ли-нейные деформации не зависят от касательных напряжений. В этом случае относительное удлинение по
направлению оси х будет обусловлено напряжением ζх |
и равно |
|
х . Напряжениям |
у |
и z в этом |
||||
|
|
|
|
|
|
Е |
|
|
|
направлении будут соответствовать удлинения |
|
у |
и |
|
z |
.По аналогии получим такие же |
|||
|
|
||||||||
Е |
E |
||||||||
|
|
|
|
|
|
||||
выражения для y и z . |
|
|
|
|
|
|
|
|
|
Таким образом, |
|
|
|
|
|
|
|
|
|
|
х |
|
1 |
|
|
|
х |
|
y |
|
z |
, |
|
|
||||||||
|
Е |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
||||
|
y |
|
1 |
|
|
y |
|
z |
|
x |
|
(4.15) |
||||||||||
Е |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|||||||
|
z |
|
1 |
|
|
z |
x |
|
y |
|
|
|||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
Е |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Угловые деформации определяются соответствующими касательными напряжениями |
||||||||||||||||||||||
|
|
|
xy |
|
, |
|
|
|
yz |
, |
|
|
zx . |
(4.16) |
||||||||
xy |
|
|
|
|
|
yz |
|
zx |
||||||||||||||
|
|
|
|
|
G |
|
|
|
G |
|
G |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Совокупность |
деформаций, |
возникающих |
по различным направлениям и в различных |
|||||||||||||||||||
плоскостях, проходящих через данную точку, называется деформированным состоянием в точке. Наряду с линейной и угловой деформацией в сопротивлении материалов приходится рассматривать иногда и объѐмную деформацию, т.е., относительное изменение объема в точке. Линейные размеры ребер элементарного параллелепипеда dx, dy, dz в результате деформации
меняются и становятся равными dx(1 x ), d y (1 y ), d z (1 z ) . Абсолютное приращение объѐма
определится разностью
V dxdydz (1 x )(1 y )(1 z ) - dxdydz .
Раскрывая скобки и пренебрегая произведениями линейных деформаций, как величинами
второго порядка малости, получим |
V dxdydz ( x |
y |
z ) . |
|||||||
Относительное изменение объѐма обозначается буквой е и определится из отношения |
||||||||||
е V |
x y z . |
|
|
|||||||
|
V |
|
|
|
|
|
|
|
|
|
Заменив деформации их выражениями по закону Гука, получим |
||||||||||
e |
1 2 |
( |
|
|
|
|
|
) |
|
(4.17) |
Е |
x |
y |
z |
|
||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Это соотношение на ряду с формулами (4.14)-(4.16) относится к обобщенному закону Гука.
4.8 Потенциальная энергия деформации
в общем случае напряженного состояния
37
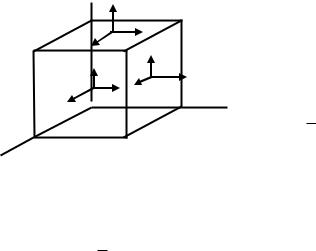
Потенциальная энергия, накопленная в элементарном объѐме, определяется суммой работ сил, распределѐнных по поверхности этого объѐма (рис.4.16). Нормальная сила x dydz на грани
перпендикулярной оси х совершит работу на перемещении |
|
|
dx , равную |
1 |
|
|
dydz |
|
dx , где |
|
- |
||||||||||||||||||||
x |
2 |
x |
x |
x |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
относительная линейная деформация вдоль оси х, вызванная всеми действующими силами. |
|
|
|||||||||||||||||||||||||||||
Аналогичные работы совершат и остальные нормальные силы, действующие по граням |
|
|
|||||||||||||||||||||||||||||
перпендикулярным осям у и х: |
|
1 |
|
|
dxdz |
|
dy , |
1 |
|
|
dxdy |
|
dz . |
|
|
|
|
|
|
|
|
||||||||||
2 |
y |
y |
2 |
z |
z |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Касательная сила yx dxdz на площадке перпендикулярной оси y совершит работу на |
|
|
|||||||||||||||||||||||||||||
перемещении |
|
dy , равную |
1 |
|
|
|
dxdz |
|
dy . Аналогичные выражения работ дают и касатель- |
|
|
||||||||||||||||||||
xy |
|
yx |
xy |
|
|
||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
z |
ζz |
|
|
|
ηzx |
|
|
|
|
|
|
|
|
|
|
ηzy |
|
dz |
|
|
|
ηxz |
|
|
|
|
|
|
|
ηyz |
ηyx |
ηxy |
ζ |
|
|
|
|
|
|
ζ |
|
|
x |
|
|
|
|
|
|
|
|
dy |
|
y |
dx |
|
|
|
|
Рис. 4.16 |
|
|
|
альной энергией и будет равна |
|
|||
ные силы, действующих на гранях перпендикулярных осям x и
z.: |
1 |
|
|
dydx |
|
dz, |
1 |
|
dzdy |
|
dx |
|
|
|
|
|
|||||||
|
2 |
|
yz |
|
yz |
|
2 |
|
zx |
zx |
|
Сумма рассмотренных работ определится выражением
dU 12 dxdydz( x x y y z z xy xy
yz yz zx zx ).
Энергия деформации, отнесенная к
dU0 12 ( x x y y z z xy xy yz yz zx zx ).
Используя выражения закона Гука для деформаций (4.15), (4.16), окончательно полу-чим
U |
|
|
1 |
2 |
2 |
2 |
2( |
|
|
|
|
|
|
|
|
) |
1 |
( 2 |
2 |
2 |
) |
|
|
(4.18) |
|||||||||
0 |
|
y |
y |
x |
|
|
|
||||||||||||||||||||||||||
|
|
2E |
x |
y |
z |
|
|
x |
|
|
|
|
|
|
z |
z |
|
|
|
2G |
xy |
|
yz |
|
zx |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для главных напряжений U |
|
|
|
1 |
|
2 |
2 |
2 |
2( |
|
|
|
) . |
(4.19) |
|||||||||||||||||||
0 |
|
|
|
2 |
1 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2E |
1 |
|
|
2 |
|
|
|
3 |
|
|
1 |
|
2 |
3 |
3 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4.9 Энергия изменения формы и объѐма
Энергия деформации расходуется на изменение формы тела и его объѐма U0 = U 0об U 0ф
Выведем выражения для этих энергий, которые потребуются в дальнейшем при изучении вопросов, связанных с пластическими деформациями и предельными напряженными состоя-ниями
|
|
|
Если тело подвергнуть всестороннему сжатию со средним напряжением |
ср |
1 2 3 , то |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
его форма изменяться не будет, а будет меняться только объѐм. В этом случае |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
U |
|
|
|
1 |
(3 2 |
2 3 2 ) |
|
3(1 20 |
2 |
|
3(1 2) |
|
( 1 |
2 |
3 )2 |
|
1 2 |
( |
|
|
|
|
|
)2 |
||||||||||||||||||||
0 об |
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
||||||||||||||||||||||||||||||||
|
|
|
|
2Е |
|
ср |
|
ср |
|
|
|
2Е |
|
ср |
|
|
|
2Е |
3 |
|
|
|
|
6 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
U |
|
|
|
1 |
2 |
2 |
2 2( |
|
|
|
|
|
|
|
|
|
|
|
|
) |
1 2 |
( |
|
|
|
|
|
)2 |
|
|
|
|
|
|
|
|
|
|||||||
0 ф |
|
|
1 |
2 |
2 |
3 |
1 |
2 |
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
2Е |
1 |
|
2 |
3 |
|
|
|
|
|
|
|
|
6Е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
38
После преобразования получим U |
|
|
1 |
( 2 |
2 |
2 |
|
|
|
(4.20) |
0 ф |
|
|||||||||
|
|
3Е |
1 |
2 |
3 |
1 2 |
2 3 |
1 3) |
|
|
|
|
|
|
|
|
|
|
|
|
39
5. Теории предельных напряженных состояний
Задачей теорий предельных напряженных состояний является оценка прочности детали при известном напряженном состоянии в еѐ опасной точке. Эта задача решается просто при простых деформациях, в частности для одноосного напряженного состояния, так как в этом случае значения предельных (опасных) напряжений достаточно просто установить опытным путем.
Предельное (опасное) напряженное состояние наступает, когда напряжения в детали достигают значений, соответствующих началу разрушения (при хрупком состоянии материала) или появлению остаточных деформаций (в случае пластичес-кого состояния материала). Испытание образцов из данного материала при одноосном растяжении или сжатии
позволяет легко установить значения опасных напряжений(ζ0 ): предел прочности для хрупких и предел текучести для пластических материалов, т.е., ζ0= ζв, или ζ0= ζт . А условие прочности в любой точке детали при линейном напряженном состоянии примет вид
, где = |
Т |
, = |
в . |
|
n |
|
n |
Если в точках детали два или все три главных напряжений ζ1, ζ2, ζ3 отличны от нуля, то в этих случаях, как показывают опыты, для одного и того же материала опасное состояние может
наступить при различных предельных значениях главных напряжений 10 , 20 , 30 , т.е., предельное
состояние будет зависеть не только от значений главных напряжений, но и от соотношений между ними. Экспериментально установить предельные значения главных напряжений очень сложно не только из-за большого количества опытов, но и из-за технических порой непреодолимых трудностей.
Другой путь решения этой задачи заключается в выборе критериев прочности (критериев предельного напряженного состояния). В этом случае вводится гипотеза о преимущественном влиянии на прочность какого-то определенного фактора, полагая, что нарушение прочности материала при любом напряженном состоянии возможно тогда, когда этот фактор достигает своего предельного значения, величина которого может быть определена на основании простых опытов на растяжение. Такой подход позволяет сопоставить сложное напряженное состояние с линейным напряженным состоянием и установить эквивалентное (расчетное) напряжение, обеспечивающее в обеих случаях одинаковый коэффициент запаса.
Выбранные рассмотренным образом критерии прочности часто называют теориями прочности. Рассмотрим некоторые из этих теорий.
Первая теория прочности – теория наибольших нормальных напряжений была предложена в1638 году Галилео Галилеем. Согласно этой теории нарушение прочности в общем случае
сложного напряженного состояния наступает, когда наибольшее нормальное напряжение достигает |
|||
своего предельного значения ζ0. В этом случае условие прочности будет следующим: ζ1 или |
|||
|
3 |
|
для материалов одинаково работающих на растяжение, сжатие; ζ1 р или |
|
|
||
|
3 |
|
с для материалов неодинаково сопротивляющихся растяжению, сжатию. |
|
|
||
Таким образом, первая теория прочности из трѐх главных напряжений учитывает толь-ко одно наибольшее, считая, что два других на прочность не влияют.
Опыты показали, что эта теория дает удовлетворительные результаты только для весь-ма хрупких материалов.
Вторая теория прочности – теория наибольших линейных деформаций была предложена в1686 году Бойли Мариоттом. Согласно этой теории нарушение прочности в общем случае сложного напряженного состояния наступает, когда наибольшая линейная деформация достигает своего
предельного значения ε0, которое определяется при простом растяжении, сжатии. Таким образом,
40
