Сопромат Лекции Филатов

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Самарский национальный исследовательский университет им. ак. С.П. Королёва (бывш. СГАУ, СамГУ)

Предмет:

Сопротивление материалов

Файл:

, EI x y II M , полученные для балок с постоянным

.pdf

Скачиваний:

Добавлен:

29.03.2016

Размер:

1.65 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 86 7 8 > Следующая >>>

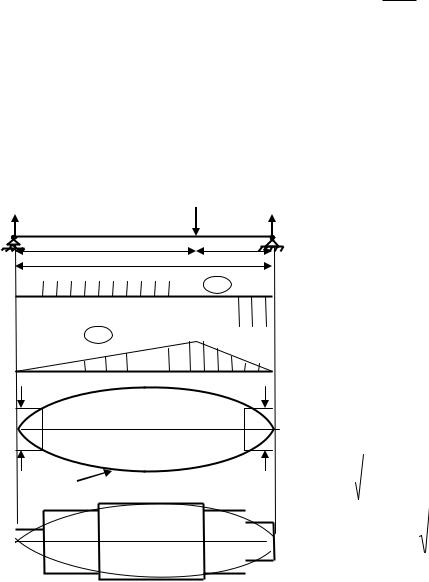
Теоретические и экспериментальные исследования показывают, что формула нормальных напряжений при чистом изгибе применима и для поперечного изгиба, если отношение длины балки к еѐ высоте ℓ/h>5.

								Вырежем часть балки, испытывающей пря-
								мой поперечный изгиб, длинной dz двумя
	F							плоскостями, перпендикулярными еѐ оси и
	F							плоскостями, перпендикулярными еѐ оси и
у								плоскостью, параллельной оси на расстоя-
								нии у от неѐ (рис.6.20). По торцам этого эле-
		dz						нии у от неѐ (рис.6.20). По торцам этого эле-
			q=q(z)					мента будут действовать нормальные напря-
			q=q(z)					жения ζ и касательные напряжения η, свя-
								жения ζ и касательные напряжения η, свя-
			dz		b(y)		dz	N+dN занные с поперечной силой зависимостью
					b(y)			Q	dA .


				η					Аотсеч
				η			dT	В элементарной теории изгиба принимается,
							dT	В элементарной теории изгиба принимается,
								что касательные напряжения по ширине се-
		ζ	η			N		чения b(y) остаются постоянными, изменяя-
			η			N		ются лишь по высоте. В плоскости сечения,
				Рис.6.20				ются лишь по высоте. В плоскости сечения,

параллельной оси балки, также будут действовать касательные напряжения согласно закону парности касательных напряжений.

Составим уравнение равновесия рассматриваемого элемента, спроектировав все силы на ось балки Z :

- N - dT + N + dN = 0 или dT = dN,

здесь dT dz b( y) , N=

dA .

Аотсеч

С учѐтом формулы

у выражение нормальной силы примет вид: N=

y dA ,

I x

Аотсеч

где y dA Sx , тогда N=

S x

, dN=

S xотсеч = dz b( y) , откуда следует

Sxотсеч

Аотсеч

I x

dz I x b( y)

Так как

Q , то окончательно получим

Q S отсеч

b( y)

(6.13)

Выведенная формула впервые была получена Д.И.Журавским и носит его имя, из неѐ следует, что знак касательных напряжений определяется знаком силы Q, а их величина по высоте сечения меняется по параболическому закону и достигает наибольшей величины на нейтральной оси.

Для прямоугольного сечения Ix=

bh3

, S

отсеч

(

y)b

(

[(

)

] ,

[(

]

6Q[(

]

bh3

Из этой формулы видно, что касательные напряжения по высоте меняются по закону

			2
квадратичной параболы. При у =	h	η = 0, при у = 0 m ax	6Qh	3	Q	.
квадратичной параболы. При у =		η = 0, при у = 0 m ax	3			.
2			4bh	2	A

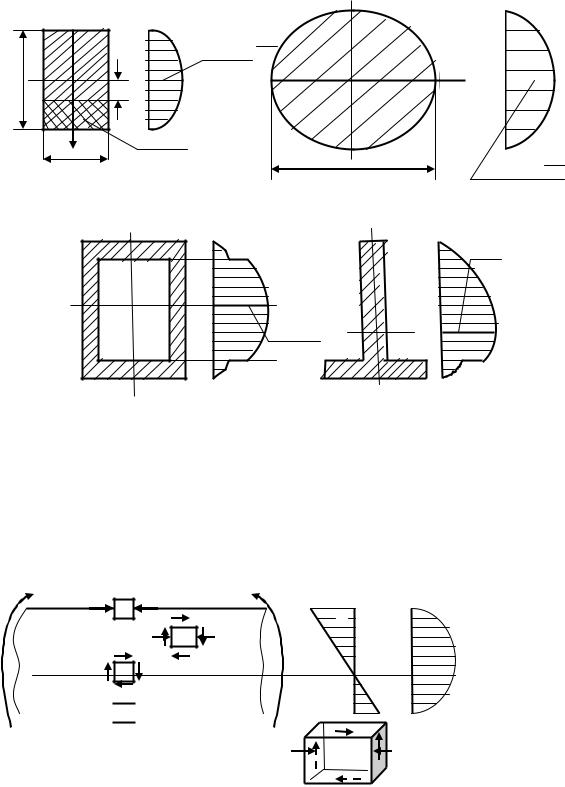
На рис.6.21 показаны эпюры касательных напряжений для прямоугольного и круглого, на рис.6.22 для коробчатого и таврового сечений.

h
		у
b	у	Аотсеч
b

m ax 3Q 2 A

d	m ax	4Q

		3A

Рис.6.21

ηmax

Рис.5.22

6.7 Расчѐт балок на прочность по допускаемым напряжениям

Из полученных формул для напряжений при поперечном изгибе	М	у ,	Q S отсеч
			x
	х		I x b( y)

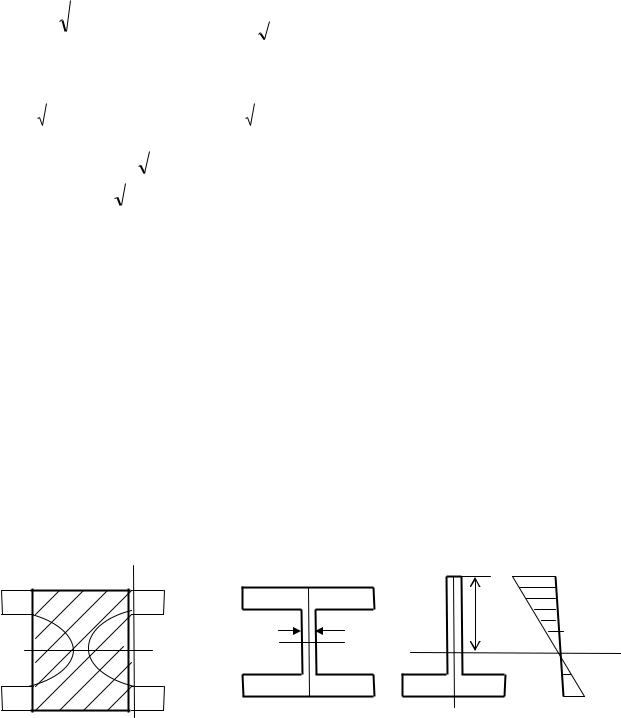
следует: в точках на поверхности балки ζ=|ζ|наиб , η=0; в точках на нейтральной оси η=|η|наиб, ζ =0; в промежутке между этими точками и нормальные и касательные напряжения отличны от нуля. Таким образом, при расчетах на прочность при изгибе по допускаемым напряжениям следует рассматривать несколько опасных точек(рис.6.23).

1	ζ	η
	3	+
	3
2

1׳

Рис.6.23

Первая опасная точка на поверхности балки, в ней линейное напряженное состояние, для которого условие прочности записывается для сечения, где М=|М|наиб

наиб	M	наиб	.



	Wx
	Wx

Вторая опасная точка рассматривается на нейтральной оси. В ней деформация чистого сдвига.

S отсеч

Условие прочности записывается для сечения, где Q=|Q|наиб

наиб

I x b( y)

При чистом сдвиге ζ1=η, ζ3=-η. Используя четвертую теорию прочности, получим

= , или

наиб

ζэкв I v = 3

наиб2

Третья опасная точка берется в промежутке между поверхностью и нейтральной осью. Так

как в этой точке плоское напряженное состояние, главные напряжения найдутся по известным формулам:

		0,5			,					0,5				. . С учетом этих выражений запишем условия
	1	0,5	2	4 2	,	2	0,		3	0,5		2	4 2	. . С учетом этих выражений запишем условия
	1		2			2			3			2
прочности:
											= ,
по третьей теории ζэквIII						=		2	4 2		= ,

по четвертой - ζэкв I v =						2		3 2 = .

Сечение, где располагается эта точка не столь определенно. Для его выбора, строго говоря, следует функцию 2 3 2 исследовать на экстремум. Обычно таким сечением является сечение, где

Qи М достаточно велики.

6.8О рациональной форме поперечного сечения балки

Согласно полученным формулам ( 6.10), (6.13) для напряжений при поперечном изгибе нормальные напряжения , изменяясь по линейному закону, равны нулю на нейтраль-ной оси и достигают наибольшего значения на поверхности балки, а касательные напряжения равны нулю на поверхности и максимальные на нейтральной оси. Рассмотренный характер распределения напряжений позволяет сделать определенный вывод о рациональной форме сечения при изгибе. Так как в балках наиболее часто нормальные напряжения значительно больше касательных, то материал, расположенный у нейтрального слоя, нагружен очень мало. Поэтому с целью его экономии и снижения веса конструкции следует выбирать такие формы сечения, у которых большая часть материала бала бы удалена от нейтральной линии, являю-щейся осью симметрии (рис.6.24 а). Из практически используемых профилей наиболее опти-мальным для материала, одинаково сопротивляющегося растяжению, сжатию, будет двутав-ровое сечение (рис. 6.24 б), для которого

толщина стенки h будет определяться величиной ηmax.

	ζ
	-
	унаиб
	h
	+
б)	в)
а)

Рис.6.24

Если материал неодинаково сопротивляется растяжению, сжатию, то опти-мальной формой сечения в этом случае будет тавровое сечение. Материал сжатию сопротив-ляется обычно лучше, чем растяжению и, следовательно, допускаемое напряжение на сжатие с будет больше

допускаемого напряжения на растяжение р , поэтому тавр следует располагать таким образом,

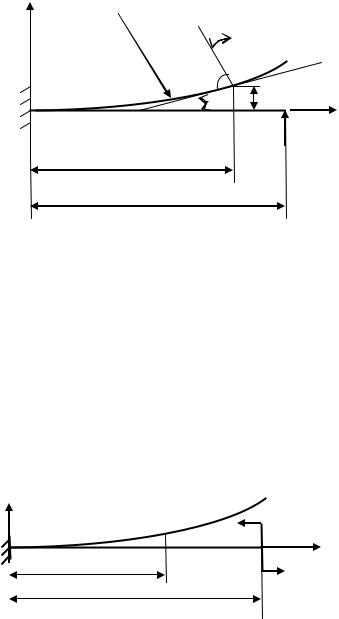
чтобы его волокна, наиболее удаленные от нейтрального слоя, располагались в сжатой области (6.24 в)

6.9 Перемещения при изгибе. Дифференциальное уравнение упругой линии балки.

При изгибе ось балки искривляется, а поперечные сечения перемещаются поступательно и поворачиваются вокруг нейтральных осей, оставаясь при этом перпендикулярными к изогнутой продольной оси (рис.6.23). Деформированная ось балки называется упругой линией, а поступательные перемещения сечений, равные перемещениям у(z) их центров тяжести сечений – прогибами балки. Прогибы у(z) и углы поворота сечений θ(z) связаны между собой. Из рис.6.22 видно, что угол поворота сечения θ равен углу θ наклона касательной к упругой линии, так как это углы с взаимно перпендикулярными сторонами. Согласно геометрическому смыслу первой производной у' =tgθ. Таким образом, tg θ = tgθ = у'.

В пределах упругих деформаций прогибы балок малы, а углы поворота не превышают 0,1рад, поэтому можно принять θ= у'.

Форма упругой линии балки определяется выражения кривизны	1	М	(α),
		ЕI x

полученной при выводе формулы нормальных напряжений.

В тоже время кривизна плоской

кривой равна

(b)

θ(z)

1 у 2

Из равенства правых частей

У(z)

выражений (α) и (b) следует

θ(z)

ЕI

1 у

Полученное уравнение называется

ℓ

дифференциальным уравнением упру-

гой линии балки. Как отмечалось выше,

Рис.6.22

при малых деформациях (у')2<<1,

поэтому этой величиной можно

пренебречь. В результате получим

дифференциальное уравнение упругой линии балки у

ЕI х .

(6.14)

Выбор знака в правой части этого уравнения определяется направлением оси У, так как от

этого направления зависит знак второй производной

При ЕIх=const, М=М( z) Е х у Е х = Мdz C , EIx y dz Mdz Cz D .

Постоянные интегрирования C и D определяются из граничных условий.

Рассмотрим дифференциальное уравнение консольной балки, загруженной парой сил на

свободном конце (рис.6.23).

EI y m,

EI y mz C,

z 2

EI y m

Cz D,

Из граничных условий при z = 0

ℓ

следует: у 0,С 0, у 0, D 0 ,

Рис. 6.23

EI y m z 2 . 2

Полученное уравнение прогибов представляет квадратичную параболу, но по выра-жению

1	М	= m	z 2	= const балка должна изогнуться по дуге окружности. В полученных результатах
			2
	ЕI x
наглядно проявляется приближенный характер уравнения					у	М	. Однако, в пределах длины

						ЕI х

балки ℓ указанные дуги параболы и окружности практически совпадают.

Если балка имеет несколько участков с различными аналитическими выражениями изгибающих моментов, то дифференциальные уравнения упругой линии также будут различны. Интегрирование таких уравнений для n участков приводит к 2n постоянных интегрирования. Для их определения к граничным условиям на опорах добавляются условия равенства проги-бов и углов поворота сечений на стыке смежных участков. Рассмотрим это на примере балки с двумя участками

(рис.6.24).

I участок: 0 z :

EIx y =

EIx y

z 3

z D

x y =

ZII

Рис.6.24

I I участок: α z b

EIx y =

z – F(z-α),

EIx y

z 2

F (z )2

CII ,

EIx y

z 3

F (z )3

CII z DII .

Здесь интегрирование идет без раскрытия скобок,

т.е., переменной интегрирования является

(z – α) а не z, что скажется только на величинах СI I , DI I

Граничные условия: zI

0, yI

0, DI

0 ;

zI I b, yI I

0 ,

Fb b 3

F ( b )3

CII b DII =0,

, y y ,

Fb 2

, C

b 2

Fb 3

y y ,

C D , D 0 ,

b 6

CI CII

F b

2b .

6 b

6.10 Балки переменного сечения и балки равного сопротивления

По конструктивным или иным причинам часто приходится выполнять балку с пере-менным сечением.

сечением на основании гипотезы плоских сечений, становятся неверными (как и сама гипот-еза). Однако, методами теории упругости показано, что если угол наклона образующей повер-хности стержня к его оси не превышает 15-20 градусов, то с достаточной для практики точ-ностью можно

пользоваться обычным условием прочности	(z)	наиб	M (z)	. Формула Журавского в этом
			M (z)
			W (z)


случае дает значительные погрешности.

Частным случаем балок с непрерывно изменяющимися размерами сечения по еѐ длине являются балки равного сопротивления изгибу.

Балкой равного сопротивления называется балка, у которой во всех сечениях

максимальное напряжение равно допускаемому: макс (z) M (z .

W (z)

Отсюда получается уравнение для определения размеров балки равного сопротивления:

W (z)	M (z)	(6.15)

Задавшись какой-либо формой сечения, размеры которого будут определяться только одним параметром, из уравнения (6.15) можно определить закон изменения этого параметра по длине балки.

Найдѐм закон изменения поперечного сечения балки равного сопротивления, изображѐнной на рис.6.25

Балка имеет два участка,

F моменты, на которых

определяются

ℓ

выражениями M1

z1 ,

, тогда согласно (6.15)

F b

Fbz

F z

(6.16)

d1наи

d2наи

Примем сечение балки круглое, для

α)

которого

d 3

, из (6.16) получим

d(z

d1 (z) 3

32Fb

(6.17)

d2 (z) 3

32F

z2 .

(6.18)

Рис.6.25

Возле опор напряжения в балке малы, а потому размеры сечения будут определяться касательными
напряжениями:			4	Q		. (6.19)
	наиб			d 2

		3			3
		3			3

Подставляя в (6.17) значения Q для каждого участка, получим значения диаметров балки на


еѐ концах (6.25 α):	d1наим		16			Q1		16		Fb		,

		3					3
		3					3

		16			Q2		16			F
d	2наим										.

				3					3

Переход к балке равного сопротивления позволяет уменьшить еѐ массу и увеличить податливость, т.е., при тех же силах увеличатся еѐ прогибы, что ей позволяет воспринимать безопасно большие энергии. Поэтому балка равного сопротивления лучше сопротивляется ударным нагрузкам.

Согласно (6.17), (6.18) рассмотренная балка будет иметь параболические очертания. Изготовление такой балки связано с большими технологическим трудностями, поэтому на практике применяют не балки равного сопротивления, а близкие к ним ступенчатые балки

(6.25 b)

Примером балки равного сопротивления может служить автомобильная рессора, масса которой в два раза меньше, а податливость в 1,2-1,4 раза больше в сравнении с балкой постоянного сечения.

Контрольные вопросы

1.Когда брус испытывает деформацию изгиба?

2.Какой изгиб называется прямым?

3.Какой изгиб называется чистым?

4.Какой изгиб называется поперечным?

5.Что такое балка?

6.Какие внутренние усилия возникают в брусе при изгибе? Как они определяются?

7.Контроль эпюр Q и М по дифференциальным зависимостям?

8.Какие напряжения возникают в балке при чистом изгибе? Как они определяются?

9.Какие напряжения возникают в балке при поперечном изгибе? Как они определяются?

10.Условие прочности балки при изгибе по нормальным напряжениям?

11.В чѐм заключается полная проверка прочности балки?

12.Какие перемещения возникают в поперечном сечении балки? Как они определяются?

13.Как определяется жѐсткость при изгибе?

7.	СДВИГ, КРУЧЕНИЕ
		7.1 Сдвиг
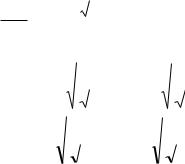
Сдвигом называется такой вид нагружения, при котором в поперечных сечениях бруса из
шести внутренних усилий отличными от нуля являются только поперечные силы.
Такой вид нагружения встречается редко. Чаще всего он сопровождается изгибающими мо-ментами.
Однако, в некоторых случаях, например, в заклѐпочных, болтовых, сварных сое-динениях имеет
место нагружение близкое к сдвигу. При этом распределение касательных напряжений
неравномерно. Так как внешние поверхности свободны от осевых нагрузок, то по закону парности
		ист		приб	касательных напряжений в верхних и
F		ист		приб	нижних точках сечения 0 . Из уравнения
F					нижних точках сечения 0 . Из уравнения
η=const		η=0			равновесия следует Q dA . Как
η=const		η=0					A
					показывают исследования, распределение
					по высоте сечения близко к равномерному
		Рис. 7.1			(η=const) , поэтому Q A и Q , где А –
		Рис. 7.1					A
							A
площадь среза.
Условие прочности :			наиб	Q ,			(7.1)
			наиб	A
				A
(0,5...0,6) - для пластических материалов и (0,8...1,0) - для хрупких материалов.
7.1.1 Чистый сдвиг и его особенности
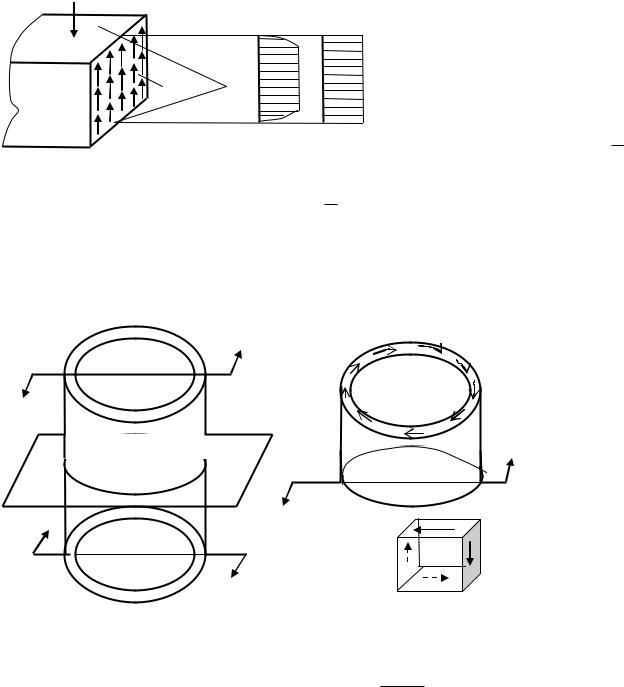
Чистым сдвигом называется такой вид плоского напряженного состояния, при котором по
							граням элементарного
							параллелепипеда,
							выделенного в
							окрестности
					η		рассматриваемой точки,
					η		действуют одни лишь
							действуют одни лишь
							касательные напряжения.
							В качестве
							примера такого
А							напряженного состояния
А							можно рассмотреть
							можно рассмотреть
							тонкостенную
						η	цилиндрическую трубку,
		М0				η	нагруженную по торцам
		М0					нагруженную по торцам
							парами сил (рис.7.2).
		Рис.7.2					Рассечем еѐ плоскостью
							А, отбросим верхнюю
часть и покажем оставшуюся нижнюю часть. В сечении действуют касательные напряжения η,
величина которых определится из условия равенства момента равномерно распределенных по
сечению внутренних сил внешнему моменту М0:					М 0	, где R – средний радиус трубки, δ – еѐ
сечению внутренних сил внешнему моменту М0:					2R 2	, где R – средний радиус трубки, δ – еѐ
толщина.
Нормальных напряжений в этом сечении не будет. Вырежем из стенки бесконечно малый
элемент в виде кубика. На его нижней грани будут действовать касательные напряжения такие же, как

и на верхней, но в противоположном направлении. На передней и задней стенках напряжений нет. Так как элемент должен находиться в равновесии, то на боковых стенках также должны быть касательные напряжения, которые создают пару сил, но направленную в противоположную сторону.

При чистом сдвиге длины ребер элементарного параллелепипеда не изменяются, а изменяются углы между гранями (рис. 7.3). Верхняя грань параллелепипеда перемещается относительно противоположной грани на величину δ, называемую абсолютным сдвигом.

а			γ
а

	а
	а		η
		Рис.7.3	η

маций tgγ = γ, тогда а = γ(рад).

δ Прямые углы изменяются на величину γ, называемую углом сдвига. Мерой деформации при сдвиге служит относительный сдвиг

	(аналогично при центральном растяжении,
а

сжатии)

Так как а = tgγ , то в силу малости дефор-

Как показывает опыт, угол сдвига γ прямо пропорционален касательным напряжениям. Эта зависимость между γ и η называется законом Гука при сдвиге и записывается выражением

	, или G .	(7.2)
G

Коэффициент пропорциональности G называется модулем сдвига (или модулем упругости второго рода). Он как и модуль продольной упругости Е измеряется в паскалях (Па) или в мегапаскалях (МПа).

7.1.2 Зависимость между упругими характеристиками материала E, G и μ

Работа сил (А), действующих по граням выделенного объѐма (рис.7.4 ) переходит в
	энергию деформации (U): A=U= 1 а 2 а , здесь а2 - сила,
	2
a	действующая на грани рассматриваемого объѐма, αγ=δ –
γ	перемещение, на котором совершается работа. Так как ,
		а
a
	то энергия деформации определится выражением U 1
δ		a3 ,
Рис. 7.4	2

																а3				1	, так как				u	1 2
а удельная энергия деформации выражением														u=	2 а3									, то			(а).
а удельная энергия деформации выражением														u=										, то			(а).
																				2		G				2 G
Эту же энергию деформации выразим через главные напряжения
u	1	2				2		2 2(										) .
u		2						2 2(					2				3	) .
	2E			1	2			3			1		2		2		3		3		1
	2E
При чистом сдвиге				,			0,				,		то u			1 2				2 (б). Из равенств (а) и (б)
При чистом сдвиге			1	,		2	0,			3	,		то u					E		2 (б). Из равенств (а) и (б)
			1			2				3

следует
						G					E
												.											(7.3)
									2(1 )			.											(7.3)

7.2. КРУЧЕНИЕ

7.2.1 Основные понятия

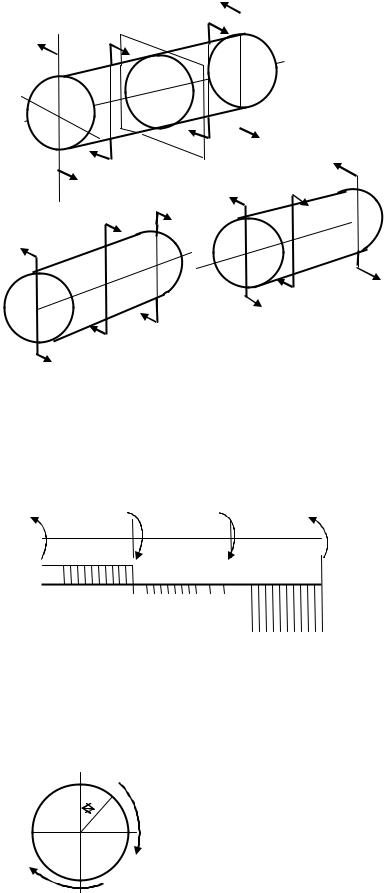
Будем рассматривать прямой брус постоянного сечения. Такой брус испытывает кручение, если он нагружен парами сил, плоскость действия которых перпендикулярна его оси.

Брус, испытывающий деформацию кручения, называется валом.

						Если вал находится в состоянии покоя или рав-
						Если вал находится в состоянии покоя или рав-
						номерного вращения, то выполняется условие
						номерного вращения, то выполняется условие
						равновесия ∑Мі = 0.
						равновесия ∑Мі = 0.
							Внутренние усилия в любом попереч-
						ном сечении, приводятся к паре сил, действую-
					М4	щей в плоскости, перпендикулярной оси бру-
						щей в плоскости, перпендикулярной оси бру-
						са, так как все внешние пары сил так же


				М3		перпендикулярны этой оси (рис.7.5). Эта
		М2			М3		пара сил называется крутящим мо-
		М2					пара сил называется крутящим мо-
	М1						ментом (Мк )и определяется мето-
							ментом (Мк )и определяется мето-
							дом сечений. Рассечѐм вал (рис.7.5)
			Мкр лев.				дом сечений. Рассечѐм вал (рис.7.5)
			к.				плоскостью и рассмотрим равнове-
			к.				сия каждой его части.
							сия каждой его части.
						М4	Равновесие левой части (рис.7.5, α):
			Мкр прав			М4	Мвн.лев. Мкр лев 0 ,
			Мкр прав				Мвн.лев. Мкр лев 0 ,
					b)		Мкр лев Мвн..лев.
							Мкр лев Мвн..лев.
М1	а)		Рис. 7.5
М1	а)
Равновесие правой части (рис.7.5, b): Мвн.пр.						Мк пр.	0 , Мк пр Мвн.пр.
							.

Из полученных выражений следует, что крутящий момент в любом сечении равен сумме моментов внешних пар сил, расположенных по одну сторону от сечения. При этом принимаются следующие правила знаков: если смотреть на сечение со стороны внешней нормали то крутящий момент принимается положительным, если он направлен против хода часовой стрелки, и отрицательным, если направлен по ходу часовой стрелки.

Эпюра крутящих моментов Мк – это график изменения его величины вдоль оси вала (рис.7.6).

М1=50кН

М =80кН

М =70кН

М =100к

МIкр = М1=50 кНм

III

Мкр,

МIIкр =М1–М2=50-80= -

30кНм

Рис.7.6

7.2.2 Связь между моментом внешних пар сил, передаваемой мощностью и числом оборотов вала

Обычно известны передаваемая мощность N и число оборотов вала n.

n об/мин	Мощность - это работа внешних сил за единицу времени : N	A	. При
θ		t

кручении вала работа определяется произведением величины внешнего

<<< < Предыдущая 1 2 3 4 56 / 86 7 8 > Следующая >>>

Соседние файлы в предмете Сопротивление материалов

#
29.03.2016516.82 Кб29Расчетно-проектировочные работы по сопротивлению материалов.pdf
#
16.03.2015613.54 Кб41СБОРНИК РАСЧЕТНО-ПРОЕКТИРОВОЧНЫХ РАБОТ ПО СОПРОТИВЛЕНИЮ МАТЕРИАЛОВ.pdf
#
29.03.2016152.26 Кб29СОПРОМАТ 2-ая 561.docx
#
16.03.2015342.37 Кб33СОПРОМАТ 1 РГР Вариант 548.docx
#
16.03.2015147.46 Кб37Сопромат 2ргр Вариант 309.doc
#
29.03.20161.65 Mб20Сопромат Лекции Филатов.pdf
#
16.03.20151.95 Mб31Сопромат Лекции Часть 1.pdf
#
29.03.2016517 Кб18Сопромат Расчетно-проектировочные работы.pdf
#
29.03.20161.34 Mб22Справочные данные. Часть 1.pdf
#
16.03.20151.48 Mб46СПРАВОЧНЫЕ ДАННЫЕ.doc