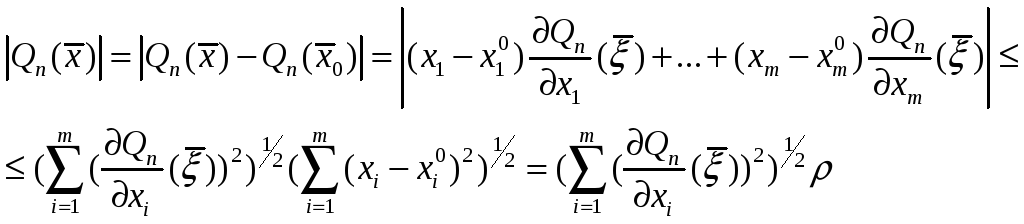-
Формула Тейлора с остаточным членом в форме Пеано
Теорема 5.
Пусть функция
u=f(x1,x2,…,xm)
n-дифференцируема
в точке
 .
Тогда существует непрерывная в точке
.
Тогда существует непрерывная в точке
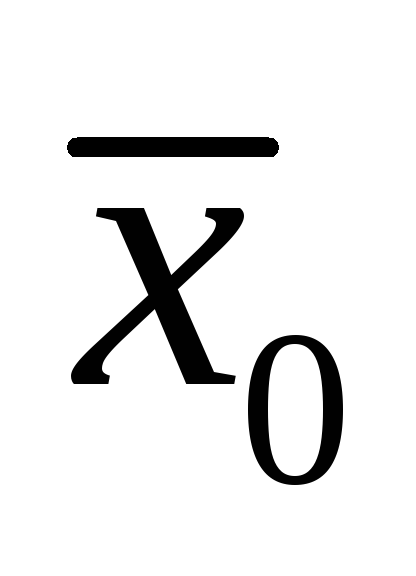 функция
функция
 такая, что
такая, что
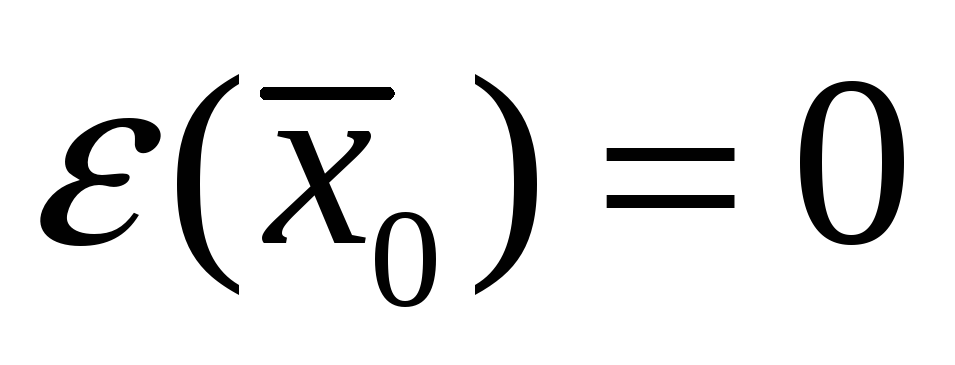 и для всех
и для всех
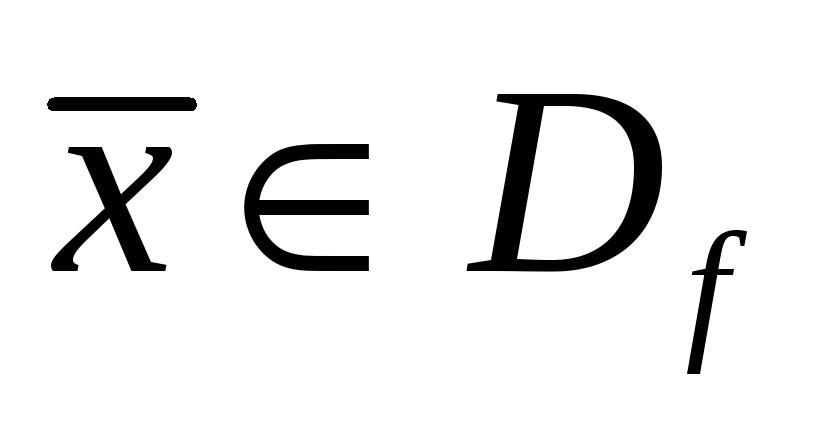 имеет место равенство
имеет место равенство
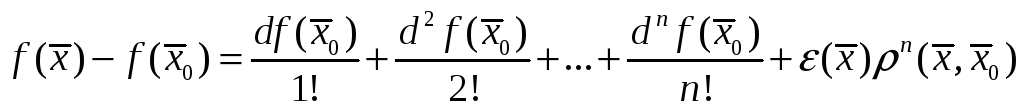 (5), где
(5), где
 .
Дифференцируемость n
раз функции f
в точке x0
предполагает её (n-1)-дифференцируемость
в некоторой окрестности точки x0.
.
Дифференцируемость n
раз функции f
в точке x0
предполагает её (n-1)-дифференцируемость
в некоторой окрестности точки x0.
Доказательство.
Положим для
всех
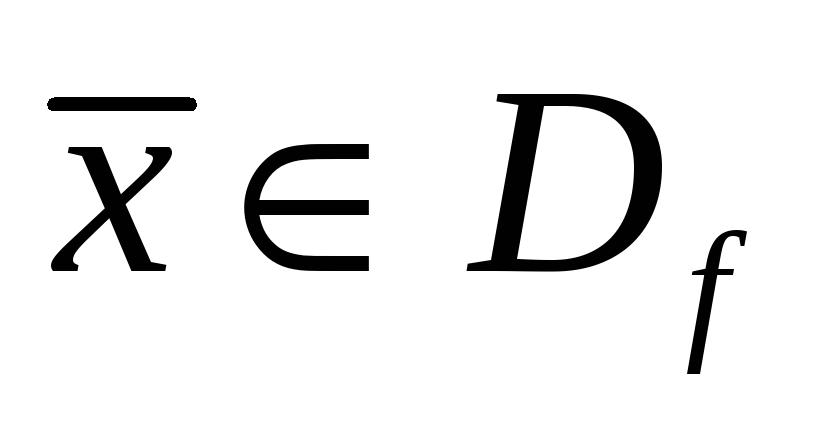
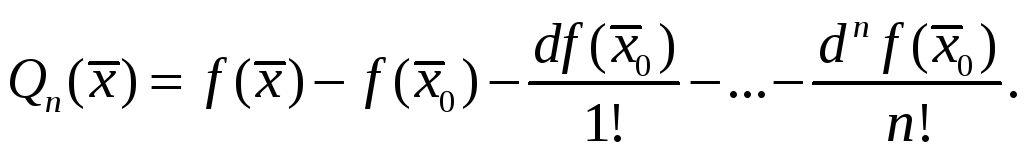 Нужно лишь доказать, что
Нужно лишь доказать, что
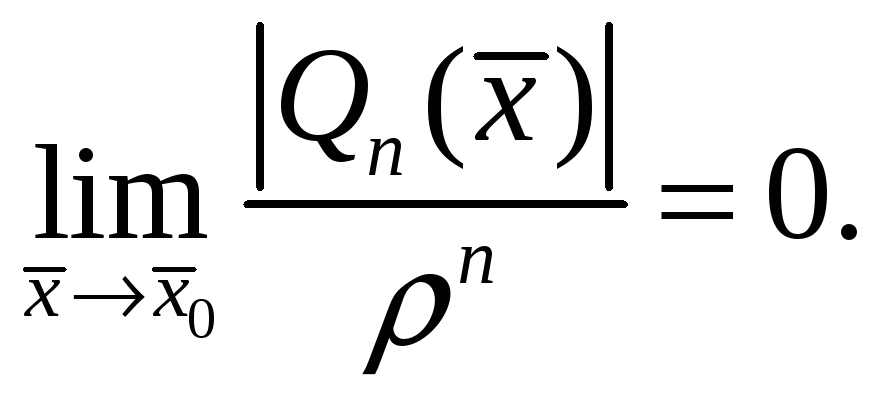
Докажем по индукции.
Для n=0
и n=1
это следует из определения соответственно
непрерывности и 1-дифференцируемости
функции f
в точке
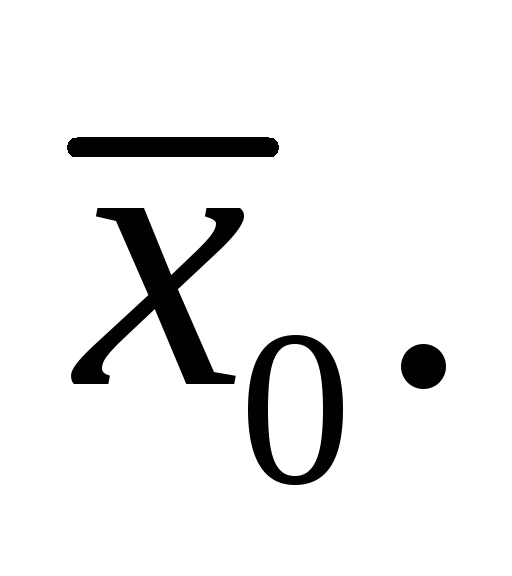
Пусть
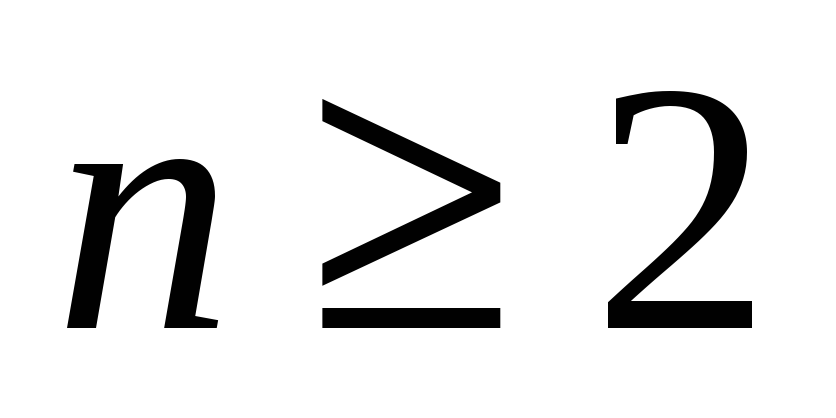 ,
и пусть теорема верна для i=n-1.
Докажем её для i=n.
,
и пусть теорема верна для i=n-1.
Докажем её для i=n.
Найдем производную
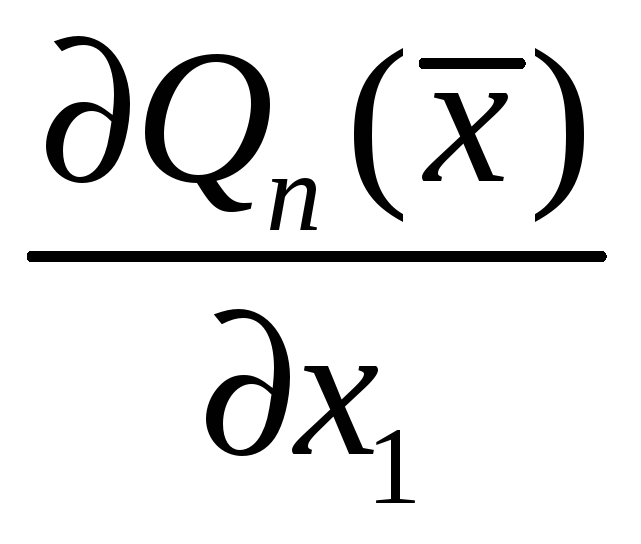 .
Предварительно убедимся, что для k=1,…,n
при фиксированных x2,x3,…,xm
.
Предварительно убедимся, что для k=1,…,n
при фиксированных x2,x3,…,xm
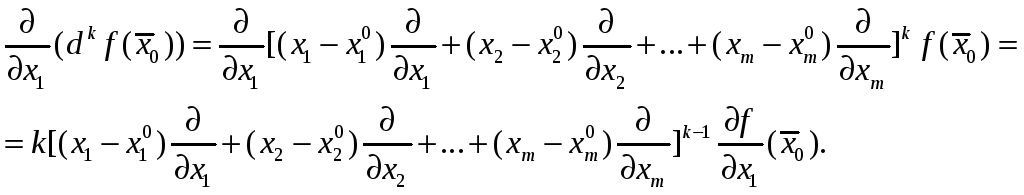
При фиксированных
x2,x3,…,xm
величину
 можно рассматривать как постоянную,
поскольку символы
можно рассматривать как постоянную,
поскольку символы
 используются для образования частных
производных функции f
в фиксированной точке
используются для образования частных
производных функции f
в фиксированной точке
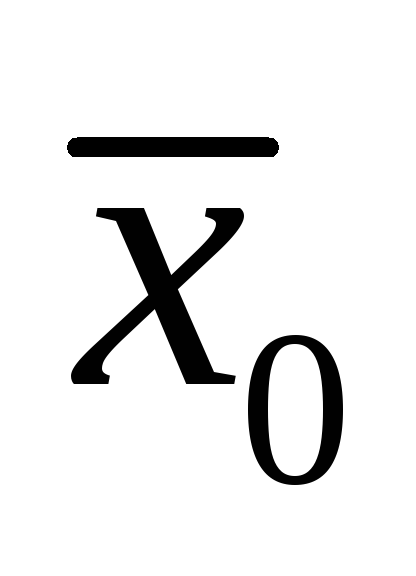 .
Поэтому
.
Поэтому
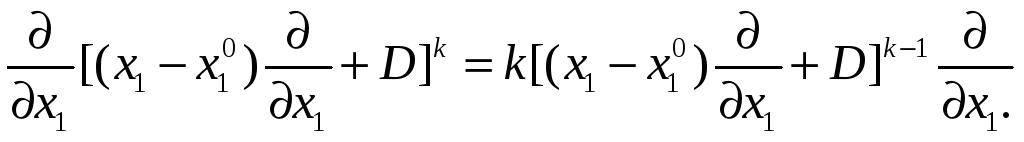 Следовательно,
Следовательно,
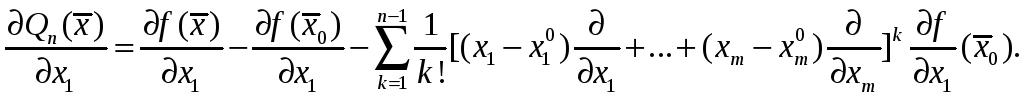 Но это есть остаточный член в формуле
Тейлора порядка n-1,
примененной к функции
Но это есть остаточный член в формуле
Тейлора порядка n-1,
примененной к функции
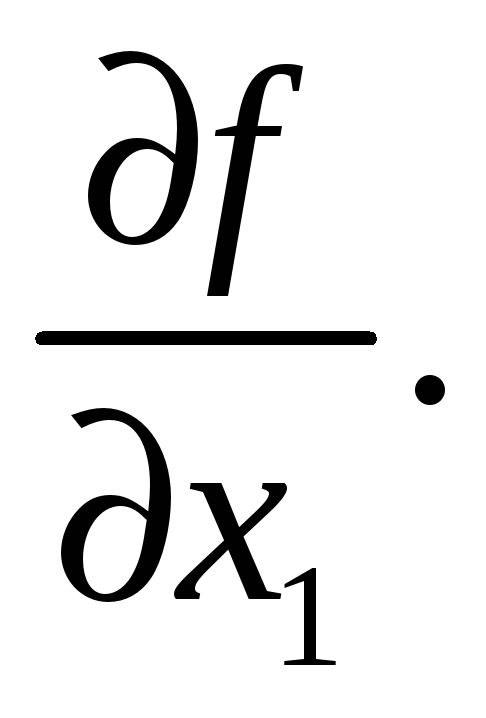 По предположению индукции
По предположению индукции
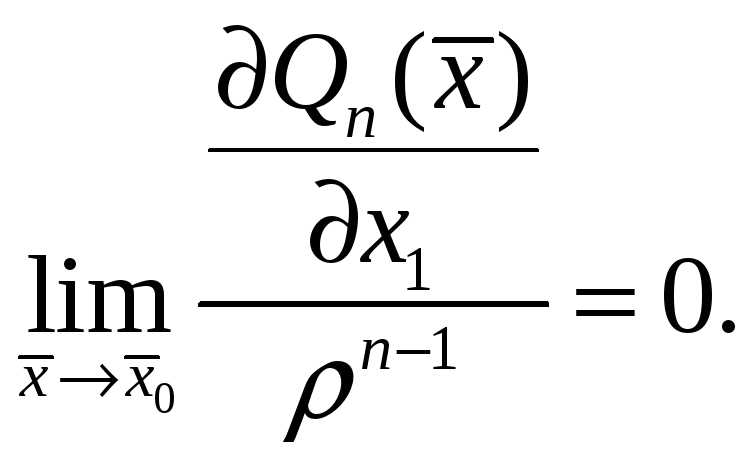 Совершенно аналогично получим, что для
i=2,…,m
Совершенно аналогично получим, что для
i=2,…,m
 Тогда взяв точку
Тогда взяв точку
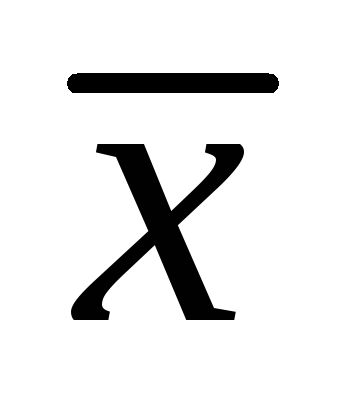 из указанной окрестности точки
из указанной окрестности точки
 и заметив, что
и заметив, что
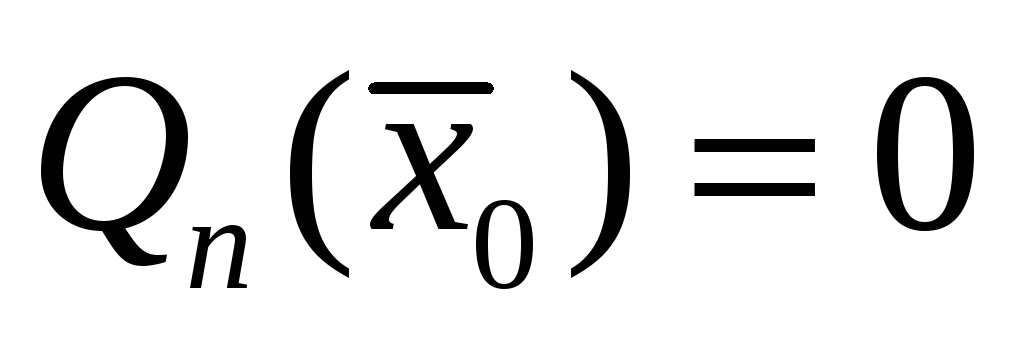 и применив формулу Тейлора порядка 1 с
остаточным членом в форме Лагранжа
будем иметь
и применив формулу Тейлора порядка 1 с
остаточным членом в форме Лагранжа
будем иметь
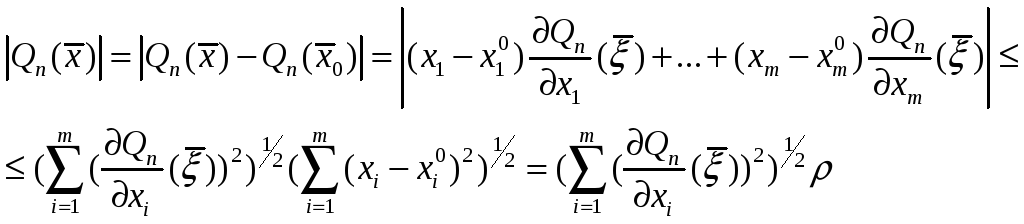
Где
 - точка, промежуточная между
- точка, промежуточная между
 и
и
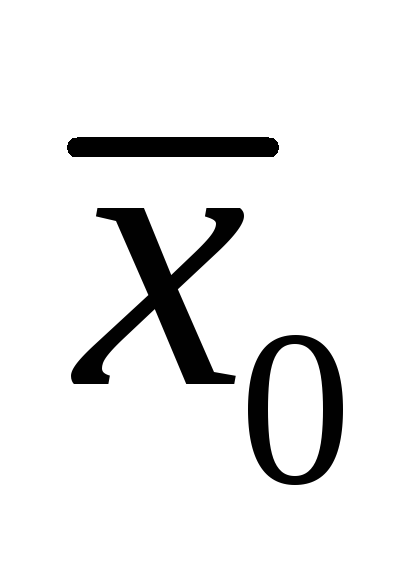 .
Следовательно,
.
Следовательно,
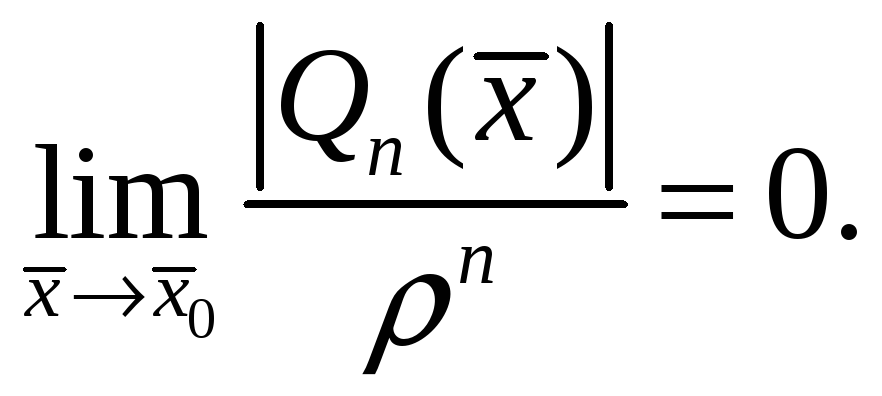 Теорема доказана.
Теорема доказана.
Замечание.
Остаточный член формулы (5) в виде
 записывают короче в виде
записывают короче в виде
 ,
где
,
где
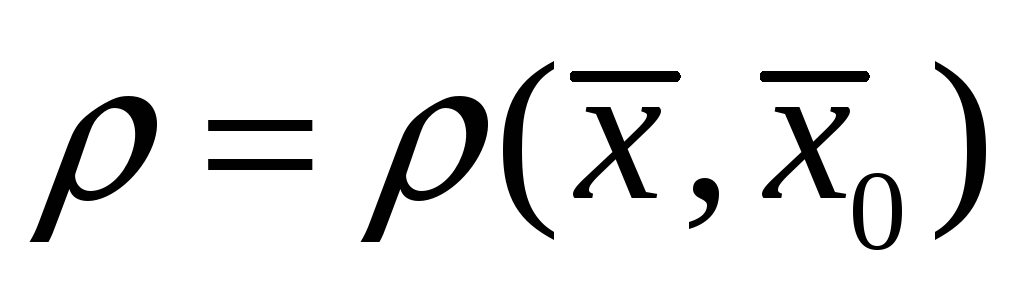 ,
и называют остаточным членом в форме
Пеано.
,
и называют остаточным членом в форме
Пеано.


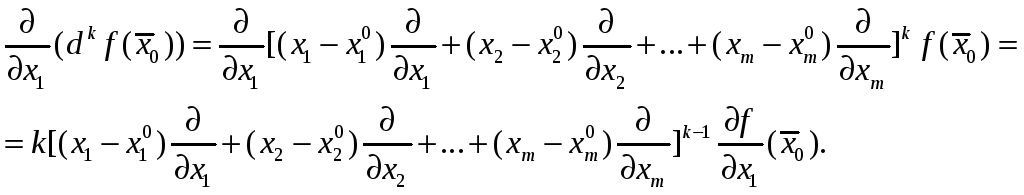
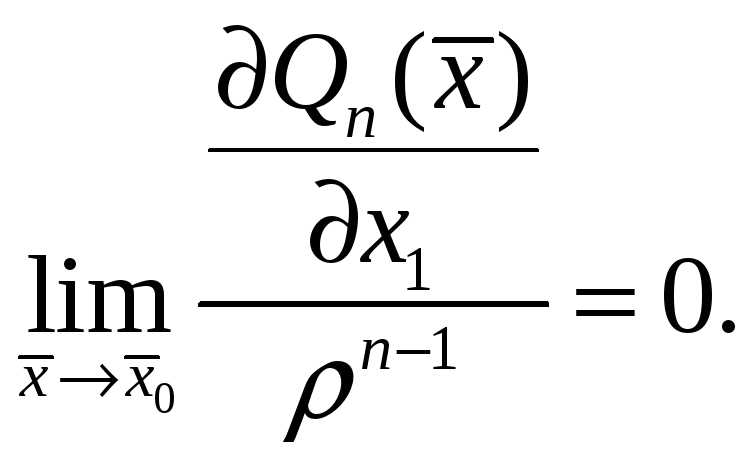 Совершенно аналогично получим, что для
i=2,…,m
Совершенно аналогично получим, что для
i=2,…,m
 Тогда взяв точку
Тогда взяв точку