Ряды фурье

Изучаемая в настоящей главе проблема разложения функции в ряд Фурье является обобщением и развитием идеи разложения вектора по базису.

Из линейной алгебры известно, что если в линейном пространстве конечной размерности выбрать некоторый базис, то любой вектор этого пространства может быть разложен по базису, т.е. представлен в виде линейной комбинации базисных векторов. Гораздо более сложными вопросами являются вопросы о выборе базиса и о разложении по базису для случая бесконечномерного пространства. В настоящей главе эти вопросы изучаются для случая евклидовых бесконечномерных пространств и для базисов специального типа (ортонормированных базисов).

Особенно подробно изучается базис, образованный в пространстве всех кусочно непрерывных на некотором сегменте функций так называемой тригонометрической системой.

§1. Ортонормированные системы и общие ряды фурье

1. Ортонормированные системы. Будем рассматривать произвольное евклидово пространство бесконечной размерности. Напомним, что линейное пространство называетсяевклидовым, если выполнены два условия:

1) известно правило, посредством которого любым двум элементам ипространстваставится в соответствии число, называемое скалярным произведением этих элементов и обозначаемое символом;

2) указанное правило удовлетворяет следующим четырем аксиомам:

1⁰ . (переместительное свойство);

2⁰ . (распределительное свойство);

3⁰ . для любого вещественного;

4⁰ . , если- ненулевой элемент;

, если - нулевой элемент.

Напомним далее, что линейное (и, в частности, евклидово) пространство называется бесконечномерным, если в этом пространстве найдется любое наперед взятое число линейно независимых элементов.

Приведем классический пример евклидова пространства бесконечномерной размерности.

Напомним, что функция называетсякусочно непрерывной на сегменте , если она непрерывна всюду на этом сегменте, за исключением конечного числа точек, в каждой из которых она имеет разрыв первого рода¹.^1

Для линейного пространства всех кусочно непрерывных на сегменте функций естественно ввести скалярное произведение любых двух функцийи, определив его равенством

(8.1)

Легко проверяется, что при таком определении справедливы первые три аксиомы скалярного произведения. Однако для того чтобы оказалась справедливой и четвертая аксиома, приходится принять дополнительную договоренность о том, чтобы значение кусочно непрерывной функции в каждой ее точке разрываравнялось полусумме правого и левого ее пределов в этой точке:

(8.2)

В самом деле, во-первых, всегда . Далее, заметим, что так каккусочно непрерывна на, то весь сегментраспадается на конечное число сегментов, на каждом из которых функциянепрерывна при условии, что в качестве значенийна концах соответствующего сегментаберутсяи. Из равенствавытекает, что для каждого сегментасправедливо равенство.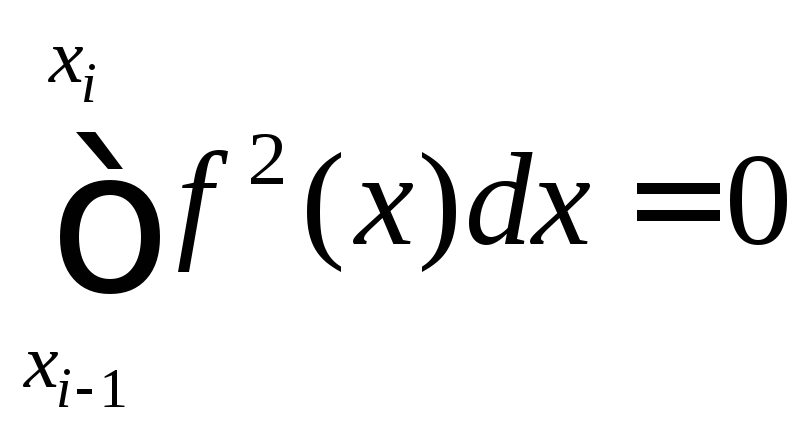

Из этого равенства и из непрерывности на сегментевытекает, что на этом сегменте. В частности,иравны нулю. Так как эти рассуждения справедливы для любого сегмента, т.е. для всех, то правый и левый пределы в любой точкеравны нулю, а отсюда в силу соотношения (8.2) и само значениев любой точкеравно нулю. Итак, функцияравна нулю во всех точках сегмента, т.е. является нулевым элементом линейного пространства всех кусочно непрерывных на сегментефункций.

Тем самым мы доказали, что пространство всех кусочно непрерывных на сегменте функций с условием (8.2) в каждой точке разрыва и со скалярным произведением, определяемым соотношением (8.1) является евклидовым пространством.

Это евклидово пространство мы в дальнейшем будем обозначать символом . Напомним теперь два общих свойства любого евклидова пространства, которыми, естественно, будет обладать и пространство:

1) во всяком евклидовом пространстве для любых двух элементов исправедливо неравенство

(8.3)

называемое неравенством Коши - Буняковского²;

2) во всяком евклидовом пространстве для любого элемента этого пространства можно ввести понятие нормы этого элемента, определив его как число, обозначаемое символоми определяемое равенством

, (8.4)

так что будут справедливы следующие три свойства:

1⁰. , причем лишь тогда, когда - нулевой элемент;

2⁰. для любого элемента и любого вещественного ;

3⁰. (8.5)

для любых двух элементов и (это неравенство называется неравенством треугольника).

В самом деле, справедливость свойства 1⁰ сразу же вытекает из (8.4) и из аксиомы 4⁰ скалярного произведения.

Для обоснования свойства 2⁰ заметим, что в силу (8.4) и аксиом скалярного произведения

.

Наконец, справедливость свойства 3⁰ вытекает из (8.4), из аксиом скалярного произведения и из неравенства Коши-Буняковского (8.3). Действительно,

.

В частности, во введенном выше евклидовом пространстве всех кусочно непрерывных на сегментефункций норма (8.4) любого элементаопределяется равенством

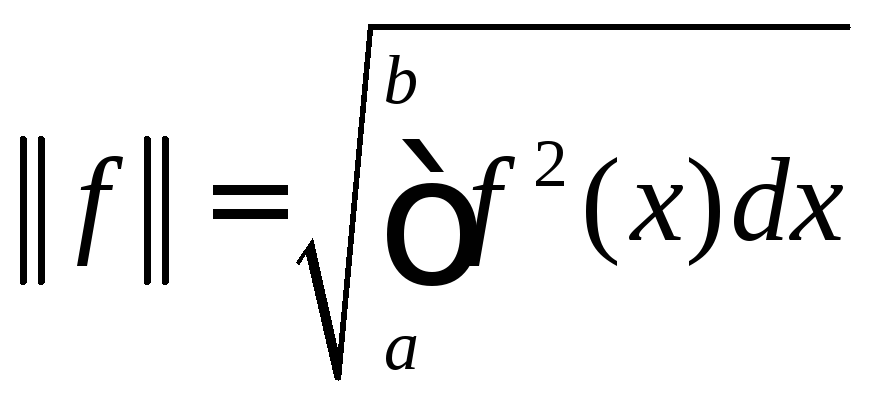, (8.6)

а неравенства Коши-Буняковского (8.3) и треугольника (8.5) принимают вид

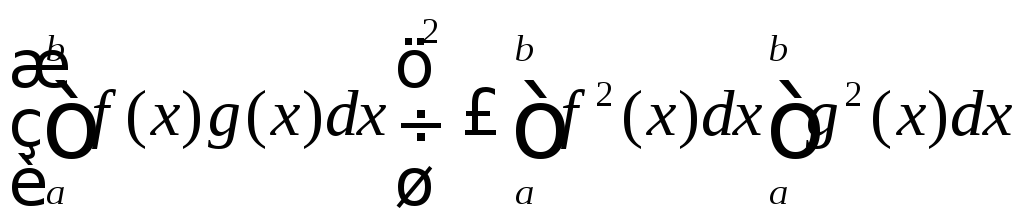; (8.7)

. (8.8)

Введем теперь в произвольном бесконечномерном евклидовом пространстве понятия ортогональных элементов и ортонормированной системы элементов.

Определение 1. Два элемента иевклидова пространства называются ортогональными, если скалярное произведениеэтих элементов равно нулю.

Рассмотрим в произвольном бесконечномерном евклидовом пространстве некоторую последовательность элементов

(8.9)

Определение 2. Последовательность (8.9) называется ортонормированной системой, если входящие в эту последовательность элементы попарно ортогональны и имеют норму, равную единице.

Классическим примером ортонормированной системы в пространстве всех кусочно непрерывных на сегментефункций является так называемаятригонометрическая система

(8.10)

Читатель легко проверит, что все функции (8.10) попарно ортогональны (в смысле скалярного произведения (8.1), взятого при ,) и что норма каждой из этих функций (определяемая равенством (8.6) при,) равна единице.

2. Понятие об общем ряде Фурье. Пусть в произвольном бесконечномерном евклидовом пространстве задана произвольная ортонормированная система элементов. Рассмотрим какой угодно элементпространства.

Определение 1. Назовем рядом Фурье элемента по ортонормированной системеряд вида

, (8.11)

в котором через обозначены постоянные числа, называемые коэффициентами Фурье элементаи определяемые равенствами

Естественно назвать конечную сумму

(8.12)

n-й частичной суммой ряда Фурье (8.11).

Рассмотрим наряду с n-ой частичной суммой (8.12) произвольную линейную комбинацию первых n элементов ортонормированной системы

(8.13)

с какими угодно постоянными числами .

Выясним, что отличает n-ю частичную сумму ряда Фурье (8.12) от всех других сумм (8.13).

Договоримся называть величину отклонением от(по норме данного евклидова пространства).

Имеет место следующая основная теорема.

Теорема 8.1. Среди всех сумм вида (8.13) наименьшее отклонение от элемента по норме данного евклидова пространства имеетn-я частичная сумма (8.12) ряда Фурье элемента .

Доказательство. Учитывая ортонормированность системы и пользуясь аксиомами скалярного произведения, можем записать:

.

Итак,

. (8.14)

В левой части (8.14) стоит квадрат отклонения суммы (8.13) от элемента (по норме данного евклидова пространства). Из вида правой части (8.14) следует, что указанный квадрат отклонения является наименьшим при (так как при этом в правой части (8.14) первая сумма обращается в нуль, а остальные слагаемые от не зависят). Теорема доказана.

Следствие 1. Для произвольного элемента данного евклидова пространства и любой ортонормированной системыпри произвольном выборе постоянныхдля любого номераn справедливо неравенство

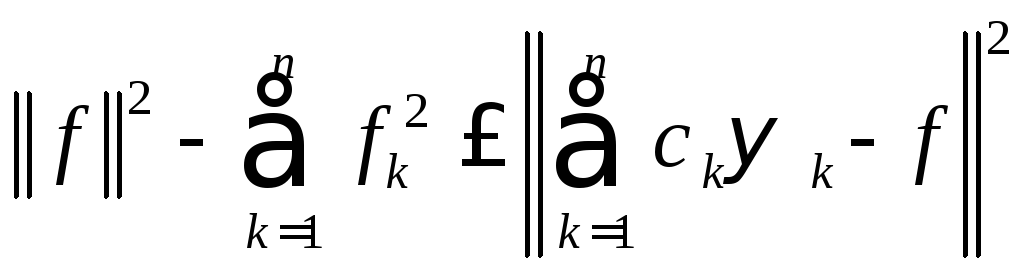. (8.15)

Неравенство (8.15) является непосредственным следствием тождества (8.14).

Следствие 2. Для произвольного элемента данного евклидова пространства, любой ортонормированной системы и любого номера n справедливо равенство

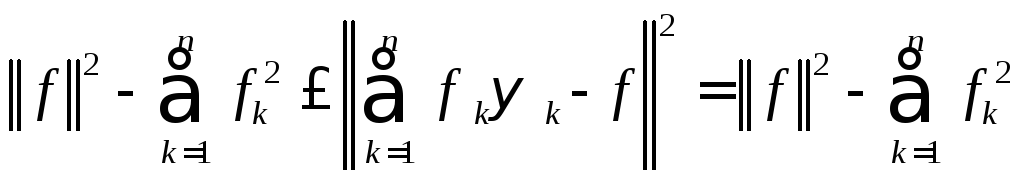, (8.16)

часто называемое тождеством Бесселя³.

Для доказательства равенства (8.16) достаточно положить в (8.14) .

Теорема 8.2. Для любого элемента данного евклидова пространства и любой ортонормированной системысправедливо следующее неравенство:

, (8.17)

называемое неравенством Бесселя.

Доказательство. Из неотрицательности левой части (8.16) следует, что для любого номера n

. (8.18)

Но это означает, что ряд из неотрицательных членов, стоящий в левой части (8.17), обладает ограниченной последовательностью частичных сумм и поэтому сходится. Переходя в неравенстве (8.18) к пределу при (см. теорему 3.13 ч. 1), получим неравенство (8.17). Теорема доказана.

В качестве примера обратимся к пространству всех кусочно непрерывных на сегменте функций и в этом пространстве к ряду Фурье по тригонометрической системе (8.10) (этот ряд принято называтьтригонометрическим рядом Фурье). Для любой кусочно непрерывной на сегментефункцииуказанный ряд Фурье имеет вид

, (8.19)

где коэффициенты Фурье иопределяются формулами

;

.

Неравенство Бесселя, справедливое для любой кусочно непрерывной на сегменте функции, имеет вид

. (8.20)

Отклонениеотпо норме в этом случае равно так называемомусреднему квадратичному отклонению

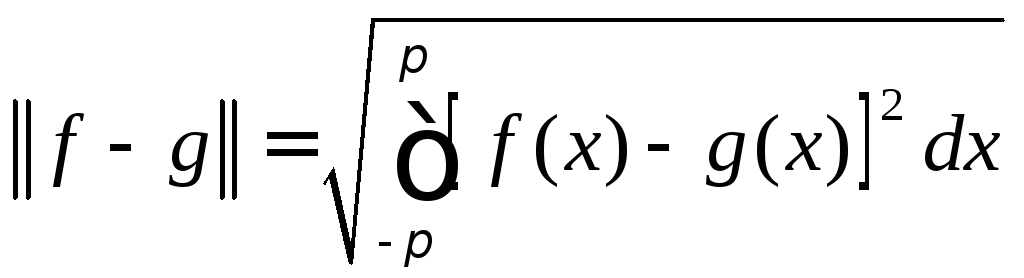. (8.21)

Отметим, что в теории тригонометрических рядов Фурье принята несколько иная форма записи как самого ряда Фурье (8.19), так и неравенства Бесселя (8.20), а именно: тригонометрический ряд Фурье (8.19) обычно записывают в виде

, (8.19^’)

где

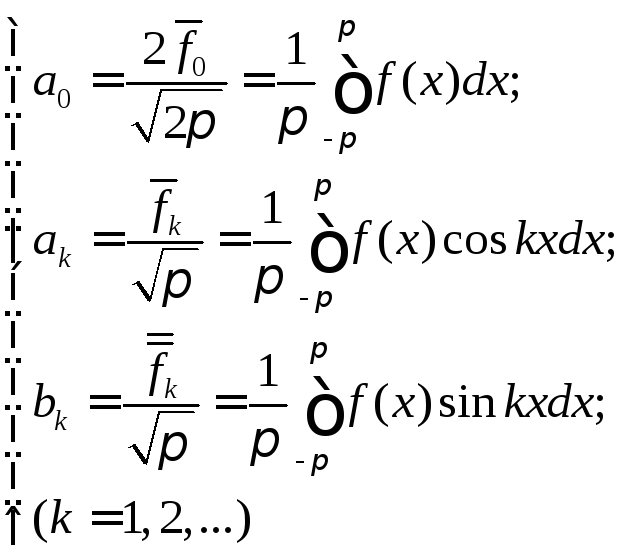. (8.22)

При такой форме записи неравенство Бесселя (8.20) принимает вид

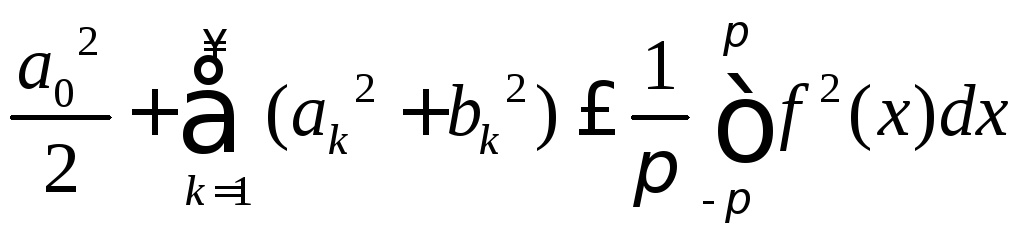. (8.20^’)

Замечание. Из неравенства Бесселя (8.20^’) вытекает, что для любой кусочно непрерывной на сегменте функциивеличиныи(называемыетригонометрическими коэффициентами Фурье функции ) стремятся к нулю при(в силу необходимого условия сходимости ряда в левой части (8.20^’)).