§ 1. Повторные интегралы от функции двух переменных.

В этой главе будет развита теория интегрирования в пространстве . Точнее, будут рассмотрены интегралы от действительных функций двух переменных.

В 1 части курса довольно подробно были изучены интегрлы от функций одного переменного. Обобщение на случай пространства может идти по двум направлениям: для вектор-функцийи функций двух переменных. В гл. 3 при построении дифференциального исчисления мы убедились, что обобщение операции интегрирования на вектор-функции одного переменного не представляет серьезного труда. Действительно, почти все изложенное в 1 части книги элементарно переносится на случай вектор-функции. Гораздо более сложным является построение теории интегрирования для функций. Здесь возникают осложнения, которые заметно усложняют положение вещей.

Начнем с того, что с помощью понятия интеграла от функции одного переменного определим повторные интегралы. Пусть дана функция , определенная всюду на, то есть. При каждом фиксированном значении первого переменногозначения функциипредставляет собой значения некоторой функции одного переменного. Допустим, что она интегрируема на прямой. Это означает, что при всех фисированных значенияхсуществует интеграл

.

Результат интегрирования зависит от того, каково значение фиксированного переменного , и тем самым представляет собой значение новой функции в точке. Допустим, что и эта функция интегрируема на прямой. Тогда интеграл

Называется повторным (первым повторным) интегралом от функции на плоскостии обозначается

.

Аналогично определяется и второй повторный интеграл:

.

Отметим, что на интегрируемость функции одного переменного и на величину интеграла не влияют значения функции, которые она принимает в конечном числе точек. Поэтому существование повторных интегралов от функции двух переменных и их величина не зависят от значений функции, которые она принимает на конечном числе прямых, параллельных координатным осям. Это обстоятельство позволяет говорить о повторных интегралах на плоскости от функции, не заданной на множестве, состоящем из точек конечного числа прямых, параллельных координатным осям.

Повторные интегралы могут быть определены и для функции с произвольной областью определения. Обозначим черезпродолжение нулем функциина плоскость, то есть

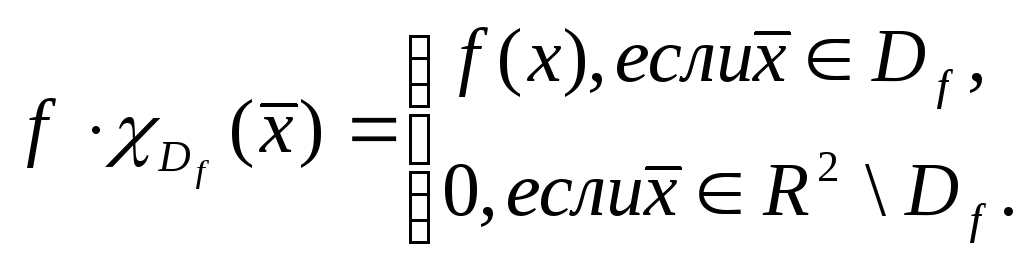
Повторные интегралы функции на плоскостиназовем повторными интегралами от функциина множестве. Эти интегралы иначе можно определить следующим образом. Пусть множество

Есть проекция множества на ось переменного, или первая проекция множества. И пусть множество

есть первое сечение множества при фиксированном значении. Очевидно, что имеет место равенство

.

Интеграл в левой части является первым повторным интегралом от функции на множествеи обозначается

Аналогично, пусть множество

Есть вторая проекция множества при фиксированном значении. Тогда интеграл

Является вторым повторным интегралом от функции на множествеи обозначается

.

Пример 1. Пусть ,

Вычислим первый и второй повторные интегралы. Так как первая проекция множества есть отрезок, а первое сечение при фисированном значенииесть отрезок, то первый повторный интеграл равен

.

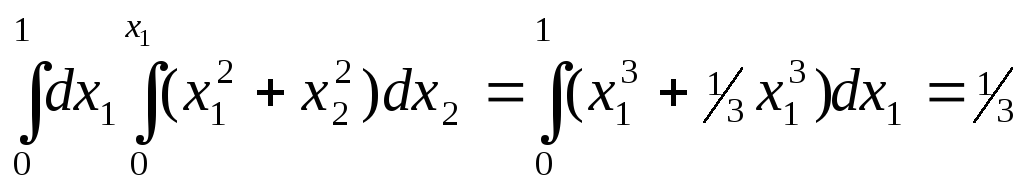Вторая проекция множества есть отрезок, а второе сечение при фиксированном значенииесть отрезок. Второй повторный интеграл равен

.

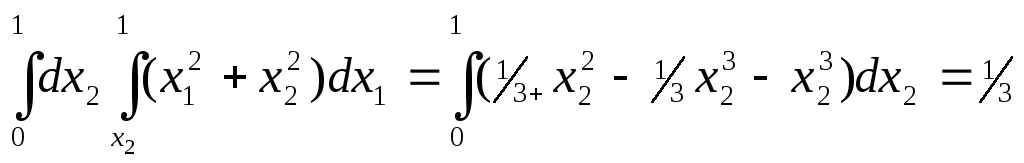Рассмотренный пример показывает, что с точки зрения вычисления повторных интегралов никакой проблемы нет. Вполне достаточно уметь вычислять интегралы от функции одного переменного. Однако часто даже интеграл от элемнтарной функции одного переменного на отрезке нельзя вычислить по формуле Ньютона-Лейбница, используя первообразную, выраженную через элементарные функции, так как она может в этом классе функций не существовать. Поэтому иногда приходится довольствоваться приближенным вычислением интеграла от функции одного переменного с помощью квадратурной формулы. В связи с этим при приближенном вычислении повторного интеграла следует заране установить его существование, исходя из свойств функции . Дело осложняется тем, что функции

, ,

Зависят от соответствующих переменных достаточно сложным образом. В полседующих параграфах проблема существования повторнх интегралов будет решаться с помощью введения двойных интегралов.

Обратим еще внимание на то, что в примере 1 первый и второй повторные интегралы равны между собой. Закономерность этого результата поясним геометрическими рассуждениями. Допустим, что функция , и вообразим в пространстве её график. Интеграл

может быть истолкован как площадь сечения тела, расположенного между графиком функции и плоскостью, плоскостью, на которой все точки имеют одну и ту же первую координату, равную. Таким образом, первый повторный интеграл есть интеграл от площадей сечений некоторого тела плоскостями, параллельными между собой, и поэтому он представляет собой объем этого тела. Второй повторный интеграл тоже дает объем этого тела. Поэтому следует ожидать, что при достаточно общих предположениях о функции повторные интегралы равны между собой. Далее докажем, что это действительно так.