§ 2. Ступенчатые функции и их интегралы.

Пусть дан прямоугольник на плоскостииесть характеристическая функция прямоугольника:

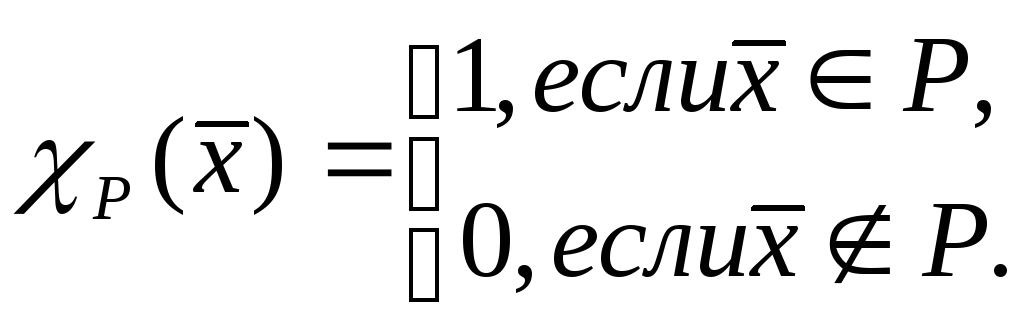
Заметим, что , где-это характеристические функции интегралов,:

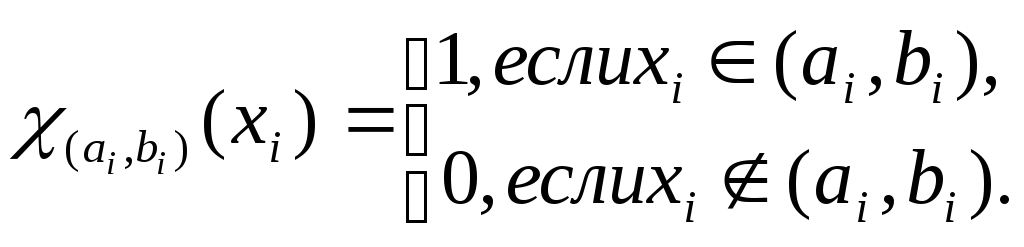
Легко подсчитать, что повторные интегралы от функции равны произведению, которое выражает площадь прямоугольника, обозначаему дальше. Это число назовем двойным интегралом от функциии обозначим одним из символов:

,

Таким образом,

.

Определение. Функция называется ступенчатой, если существует конечное число прямоугольникови числатакие, что равенство

.

имеет место при всех , за исключением, быть может, точек, расположенных на конечном числе прямых, параллельных координатным осям. В этом случае мы будем далее писать

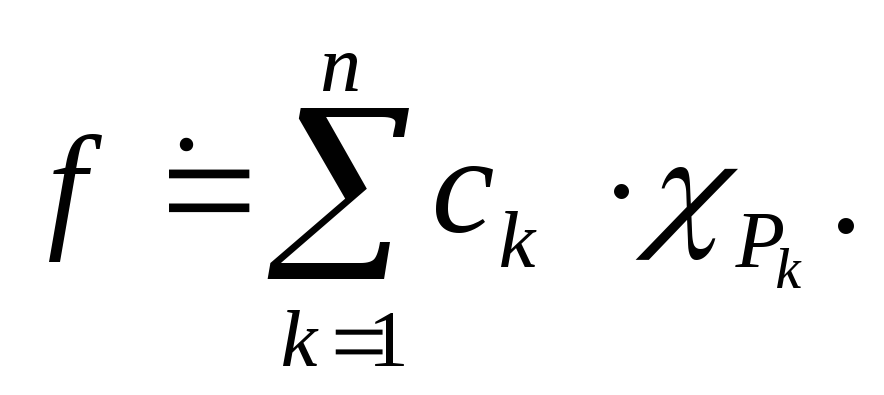
Аналогичный смысл будем придавать обозначениям .

Величину

назовем интегралом, или дойным интегралом от функции и будем обозначать одним из символов:

, .

Из определения 1 сразу следует, что если -ступенчатые функции,, то функциитакже ступенчатые.

Покажем, что интеграл от ступенчатой функции совпадает с обоими повторными интегралами.

Теорема 1. Если функция ступенчатая, то

.

Доказательство.

Пусть Тогда по определению интеграла от характеристической функции прямоугольника и интеграла от ступенчатой функции имеем

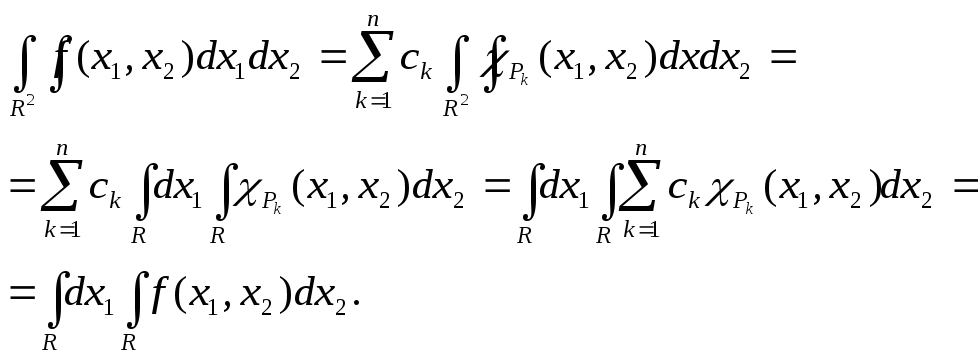
Аналогично доказывается, что

.

Теорема доказана.

Следствие 1. Интеграл от ступенчатой функции определен однозначно.

Следствие 2. Если функция ступенчатая и, то

.

Это свойство называется свойством положительности интеграла.

Следствие 3. Если функции иступенчатые,, то

, .

Это свойство называется свойством линейности интеграла.

Следствие 4. Если функции иступенчатые,, то.

Это свойство называется свойством мононтонности интеграла.

Все эти следствия доказываются с помощью теоремы 1 и аналогичных свойств интеграла от функции одного переменного. Возможно получить и непосредственные доказательства этих утверждений, исходя из определения интеграла от ступенчатой функции.

§ 3. Верхний интеграл Дарбу и его свойства.

Определение. Замыкание множества точек, в которых функция отлична от нуля, называется носителем функциии обозначается символомsupp f. Функция называется финитной, если ее носитель есть ограниченное множество.

Определение. Пусть функция ограничена и финитна. Тогда число

,

(нижняя грань берется по всем ступенчатым функциям , обладающим свойством) называется верхним интегралом Дарбу функции.

Теорема 1. У каждой ограниченной финитной функции существует верхний интеграл. Причем, если supp f ,

, , то.

Доказательство. Рассмотрим множество чисел , где ступенчатые фунцииобладают свойством, а-ограниченная финитная функция. Функцияявляется ступенчатой и. Следовательно, рассматриваемое числовое множестов не пусто, ему принадлежит число. Кроме того это множество ограничено снизу числом, так как если, тои. Поэтому числовое множество должно иметь конечную нижнюю грань, то есть существует верхний интеграл. При этом справедливы неравенства

.

Теорема доказана.

Следующее следствие носит название теоремы о среднем.

Следствие 1. Если функция непрерывна на замкнутом прямоугольникеиsupp f , то существует точка , такая, что

.

Доказательство. По теореме 1

.

По теореме о промежуточном значении непрерывной функции на линейно связном множественайдется точкатакая, что, то есть.

Покажем, что для ступенчатых функций понятие верхнего интеграла совпадает с прежним понятием интеграла.

Теорема 2. Если функция ступенчатая, то.

Доказательство. Пусть -ступенчатая функция. Если-произвольная ступенчатая функция, обладающая свойством, то. Перейдя в левой части неравенства к нижней грани по всевозможным функциям, получим неравенство. В качестве ступенчатой функции, удовлетворяющей условию, можно взять функцию. Тогда по свойству нижней грани. Следовательно,. Теорема доказана.

Для верхнего интеграла сохраняется свойство монотонности. Докажем это.

Теорема 3. Если и-ограниченные финитные функции и, то.

Доказательство. Пусть ступенчатая функция обладает свойством. Тогдаи поэтому по свойству нижней грани. Перейдя в правой части неравенства к нижней грани по всевозможным функциям, получим неравенство. Теорема доказана.

Интеграл от ступенчатой функции обладал свойством линейности, которое объединяет свойства аддитивности и однородности. Верхний интеграл от произвольной огрниченной финитной функции теряет эти свойства, но не совсем, а наполовину. Следующая теорема выражает свойство полуаддитивности, или выпуклости верхнего интеграла.

Теорема 4. Если и-ограниченные финитные функции, то

.

Доказательство. Пусть . По свойству нижней грани найдутся ступенчатые функции, такие, чтои. Так как, то

.

Перейдя к пределу при , получим неравенство. Теорема доказана.

Следующая теорема выражает свойство положительной однородности верхнего интеграла.

Теорема 5. Если -ограниченная финитная функция,, то

.

Доказательтво. При утверждение очевидно. Пусть. Тогда

===.

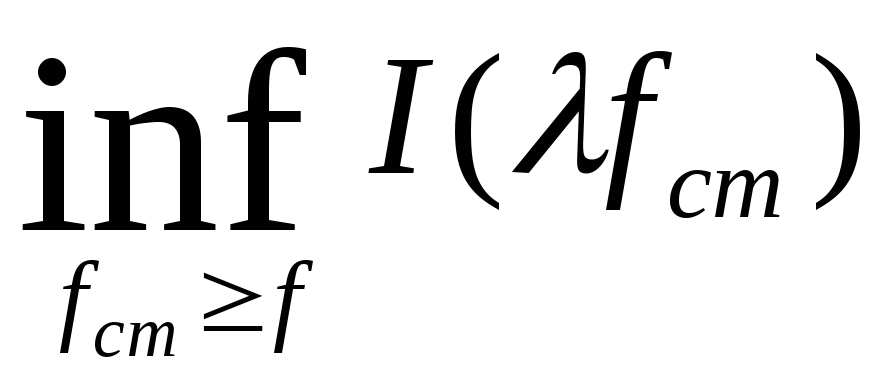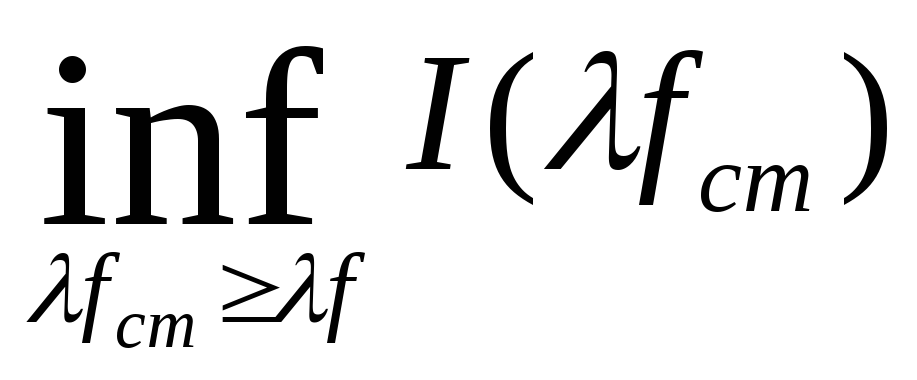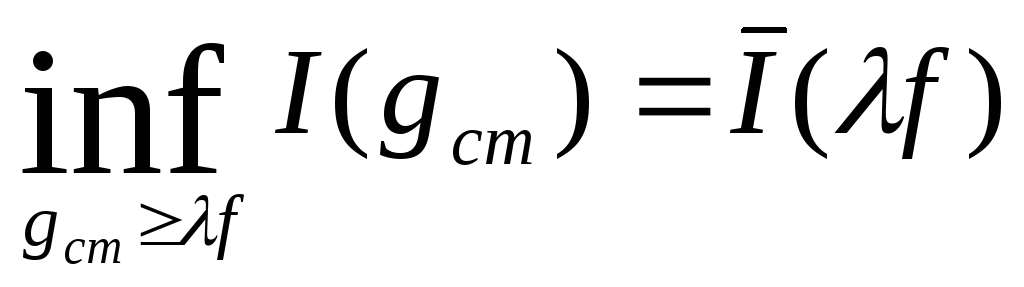Теорема доказана.