Материалы по мат. анализу для самостоятельного обучения / Глава 5 Степенные_ряды

Степенные ряды.

Определение. Степенным рядом называется функциональный ряд вида:

а₀+а₁х+ а₂х²+…=а_nxⁿ (1),

где а₀, а₁,… -- вещественные числа, называемые коэффициентами ряда.

Выясним, как устроена область сходимости степенного ряда.

Заметим, что любой степенной рядсходится в точке х=0, причем существуют степенные ряды, сходящиеся только в этой точке (например, ряд n!xⁿ).

Рассмотрим числовую последовательность (). Могут представляться два случая:

1. она является неограниченной;

2. она является ограниченной.

В первом случае – =+∞,

во втором – 0≤ <+∞.

Докажем следующую замечательную теорему.

Теорема 1 (Коши-Адамара).

Пусть =l . Тогда

1. если l=+ , то ряд (1) сходится лишь в точке х=0;

2. если 0<l<+, то ряд (1) абсолютно сходится в точках х, удовлетворяющих условию |x|<, и расходится в точках х, удовлетворяющих условию |x|>;

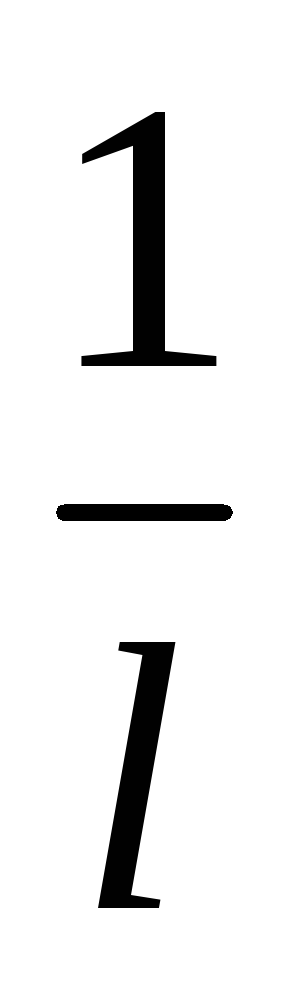3. если l=0, то ряд (1) абсолютно сходится во всех точках хR.

Доказательство.

Очевидно, что

=l|x|

Если l=0, то для любого хR l|x|=0 и по радикальному признаку Коши ряд абсолютно сходится.

Если 0<l<+, то при всех х, удовлетворяющих |x|<, (l|x|<1) по радикальному признаку Коши ряд абсолютно сходится, а при всех х, удовлетворяющих |x|> – расходится.

Аналогично при l= + ряд расходится при любом х≠0.

Теорема доказана.

Определим число R=, если 0<l<+; R=0, l= и R=+, если l=0.

Это число R называют радиусом сходимости степенного ряда, а интервал

(-R, R) при R>0 – интервалом сходимости.

Отметим, что в точках х=-R и х=R степенной ряд может сходится, а может расходится.

Замечание. Если воспользоваться признаком Даламбера для последовательности степенного ряда, то можно придти к формуле:

||, если этот предел существует.

Выясним, какими свойствами обладает сумма степенного ряда.

Теорема 2. Пусть радиус сходимости степенного ряда R>0. Если 0<r<R, то ряд (1) равномерно сходится на отрезке [-r,r], т.е. при |x|≤r.

Доказательство.

В силу теоремы 1 ряд (1) сходится в точке х=r, т.е. сходится ряд а_nrⁿ. Этот числовой ряд мажорирует при любом х из отрезка [-r,r]. На основании признака Вейерштрасса ряд (1) равномерно сходится на отрезке [-r,r]. Теорема доказана.

Следствие. В условии теоремы сумма ряда является функцией непрерывной на отрезке [-r,r].

Теорема 3. Сумма степенного ряда внутри интервала сходимости является непрерывной функцией.

Доказательство.

Пусть S(x) – сумма ряда (1), R – радиус сходимости. Пусть |x|<R, тогда найдется r такое, что |х|<r<R. В силу следствия теоремы 2 S непрерывна на отрезке [-r,r], а следовательно и в точке х. Теорема доказана.

Теорема 4. Пусть R>0 – радиус сходимости степенного ряда (1), |x|<R. Тогда на отрезке с концами 0 и х сумма ряда интегрируема и

=a₀x+x²+…+xⁿ+…,

Причем новый ряд имеет тот же радиус сходимости.

Доказательство.

Для любого х, удовлетворяющего условию |x|<R, найдется r такое, что |х|<r<R. Согласно теореме 1 на [-r,r] ряд сходится равномерно, и следовательно, его можно интегрировать почленно. Но тогда этот ряд можно почленно интегрировать и на отрезке с концами 0 и х. В результате почленного интегрирования получаем степенной ряд

a₀x+x²+…+xⁿ+… ,

радиус сходимости которого, есть величина обратная верхнему пределу

==, т.е. R.

Теорема доказана.

Теорема 5. Пусть радиус сходимости степенного ряда (1) R>0. Тогда в интервале сходимости сумма ряда S(x) дифференцируема и

S’(x)= ,

Причем полученный ряд имеет тот же радиус сходимости.

Доказательство.

Возможность почленного дифференцирования вытекает из теоремы о дифференцируемости суммы функционального ряда.

Так как =,

То радиус сходимости полученного ряда то же число. Теорема доказана.

Следствие. Степенной ряд в интервале сходимости можно почленно дифференцировать сколько угодно раз. Все получаемые ряды имеют тот же радиус сходимости.

Будем говорить, что функция f(x) на интервале (-R, R) может быть разложена в степенной ряд, если существует степенной ряд, сходящийся к f(x) на указанном интервале.

Пусть f(x)= а₀+а₁х+ а₂х²+…+а_nxⁿ+…

Дифференцируя этот ряд почленно n раз, получим

f⁽ⁿ⁾(x)=n!a_n+a_n+1(n+1)n…2x+…

отсюда

f⁽ⁿ⁾(0)= a_n n!

или

a_n=, nN, a₀=f(0). (*)

Степенной ряд, коэффициенты которого определяются по формуле (*), называется рядом Тейлора функции f. Можно сделать вывод, если функция f может быть разложена на интервале (-R, R) в степенной ряд, то этот ряд является ее рядом Тейлора.

Для того, чтобы функция могла быть разложена в ряд Тейлора на интервале (-R, R) необходимо и достаточно, чтобы остаточный член формулы

Тейлора – Маклорена для этой функции стремился к нулю на указанном интервале.

Поскольку остаточные члены в формуле Маклорена для функций e^x, cos x и sin x стремятся к нулю на всей числовой прямой, для функции ln(1+x) стремится к нулю на полуинтервале (-1,1], то справедливы разложения:

e^x= , хR,

cos x=, хR,

sin x=, хR,

ln(1+x)= , -1<x≤1

Кроме того

(1+x)^α =, α>0, -1<x<1.

4