§ 3. Кратный интеграл фурье

Здесь мы дадим лишь самые начальные понятия о кратном ин» теграле Фурье. Пусть функция N переменных f(x)=f(x₁, х₂, ... , х_N), , такова, что существует несобственный интеграл

Назовем преобразованием (образом) Фурье такой функции f(х) величину

где (х,λ) означает скалярное произведение векторов x=(x₁, х₂, ... ..., x_N) и λ =( λ₁, λ₂, …, λ_N), т. е.

Точно так же, как в § 1, можно показать, что g(λ) является непрерывной функцией λ в Е^N и стремится к нулю при 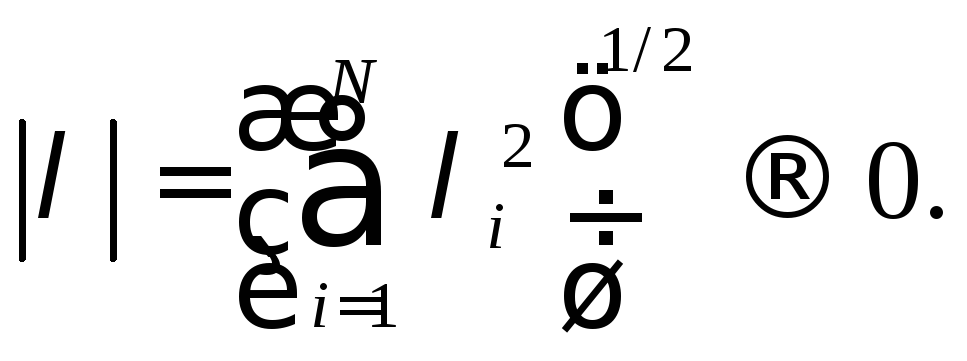Предел

при условии, что он существует, называется разложением функции f(x) в N-кратный интеграл Фурье. С помощью перехода к пределу получается (так же, как в случае одной переменной х) формула обращения

где

x=(x₁, x₂,…,x_N), λ=(λ₁, λ₂,…, λ_N ).

1^¹ Т.е. в каждой точке разрыва у функциисуществует конечный левый и конечный правый пределы.

2 Для доказательства неравенства (8.3) заметим, что для любого вещественного в силу аксиомы 4⁰ скалярного произведения справедливо неравенство , которое в силу аксиом 1⁰ – 4⁰ эквивалентно неравенству . Необходимым и достаточным условием неотрицательности квадратного трехчлена, стоящего в левой части последнего неравенства, является неположительность его дискриминанта, т.е. неравенство, которое эквивалентно неравенству (8.3).

3 Фридрих Вильгельм Бессель – немецкий астроном и математик (1784-1846).

4 М.А.Парсеваль – французский математик (1755-1836).

5 Под тригонометрическими функциями в данном случае понимаются косинус и синус.

6 Так как эта функция удовлетворяет тем же условиям, что и полученная после продолжения функция .

7 А следовательно (в силу теоремы 8.5), и полной

8 Первый пример такой функции был построен французским математиком Дю Буа Раймоном в 1876г.

9При этом функция может оказаться неопределенной в конечном числе точек сегмента. В этих точках мы доопределим ее произвольным образом (например, положим равной полусумме правого и левого предельных значений).

10Например, можно положить функцию в указанных точках равной полусумме правого и левого предельных значений.

11При интегрировании по частям следует разбить сегмент на конечное число не имеющих общих внутренних точек частичных сегментов, на каждом из которых производная непрерывна, и, беря формулу интегрирования по частям для каждого из этих частичных сегментов, учесть, что при суммировании интегралов по всем частичным сегментам все подстановки обратятся в нуль (вследствие непрерывности на всем сегменте и условий ).

12 Мы исходим из элементарного неравенства , вытекающего из неотрицательности величины .

13 При интегрировании по частям сегмент следует разбить на конечное число не имеющих общих внутренних точек частичных сегментов, на каждом из которых непрерывна, и учесть, что при суммировании интегралов по всем частичным сегментам все подстановки дают нуль.