4. Дифференцирование сложной функции

Рассмотрим сложную функцию , где (3)

Теорема 4. Пусть функции (3) дифференцируемы в точке , а функция u=f(x₁,x₂,…,x_m) дифференцируема в точке , где Тогда сложная функция дифференцируема в точке , при этом частные производные вычисляются по формулам

Доказательство. Возьмем приращения . Им соответствуют приращения функций (3) в точке . Приращениям, в свою очередь, соответствует приращение функций u=f(x₁,x₂,…,x_m) в точке . Так как функция f дифференцируема в точке , то . В силу дифференцируемости функций (3) в точке

Подставив последние равенства, получим:

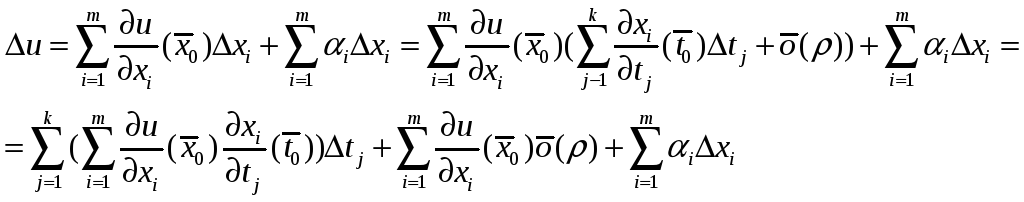
Осталось доказать, что последние две суммы представляют собой величину . Очевидно, что . Далее, . Так как , то .

Итак, , что означает дифференцируемость сложной функции, причем . Теорема доказана.

Замечание. Рассмотрим важный частный случай, когда . Тогда .

5. Дифференциал функции многих переменных. Инвариантность формы первого дифференциала.

Определение. Дифференциалом дифференцируемой в точке функции u=f(x₁,x₂,…,x_m) называется главная линейная относительно приращений аргументов часть приращения этой функции в точке , то есть .

Используя теорему 1, перепишем .

Введем понятие дифференциала независимой переменной . Под дифференциалом независимой переменной можно понимать любое число. Будем брать это число, равным приращению независимой переменной . Тогда (4)

Докажем, что формула (4) справедлива и в том случае, когда аргументы x₁,x₂,…,x_m сами являются дифференцируемыми функциями некоторых новых переменных t₁,t₂,…,t_k. Это свойство называют свойством инвариантности формы первого дифференциала.

Пользуясь теоремой 4, получим

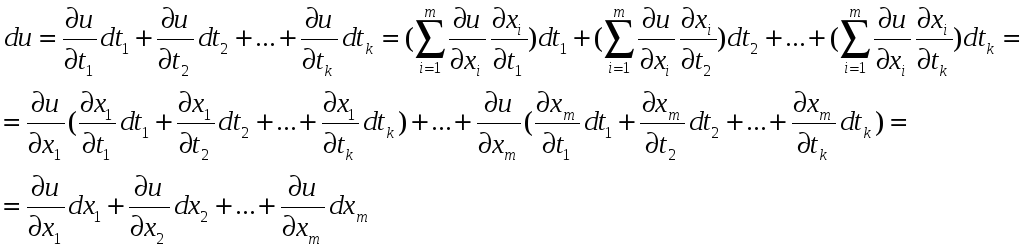
Свойство инвариантности формы первого дифференциала позволяет установить следующие правила дифференцирования. Пусть u и v – дифференцируемые функции. Тогда

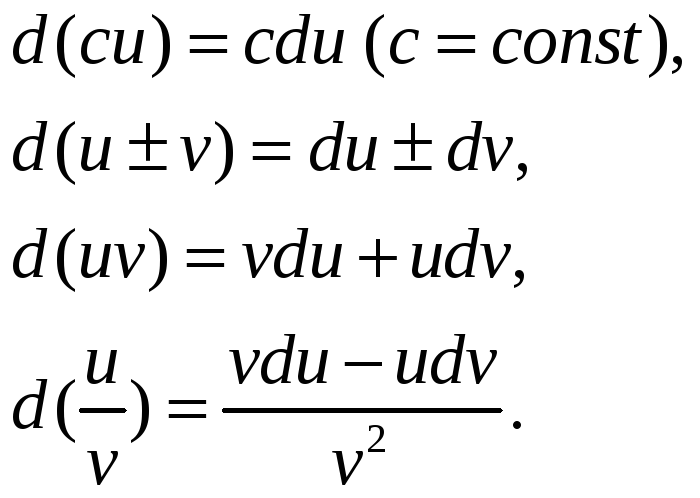
Докажем, например, справедливость третьего равенства. Рассмотрим функцию двух переменных u и v. Тогда В силу инвариантности формы первого дифференциала выражение будет дифференциалом функции и в случае, когда u и v сами являются дифференцируемыми функциями каких-либо переменных.

Задание. Доказать остальные равенства.

6. Производная по направлению. Градиент.

Начнем с рассмотрения функции трех независимых переменных . Пусть эта функция определена в некоторой окрестности точки M₀(x₀,y₀,z₀) и дифференцируема в этой точке.

Рассмотрим всевозможные лучи, выходящие из точки M₀(x₀,y₀,z₀). Каждый такой луч задается единичным вектором .

Взяв на прямой, содержащей этот луч, точку M(x,y,z), рассмотрим вектор , где l – длина отрезка M₀M. С другой стороны, . Сопоставляя эти равенства, получим:

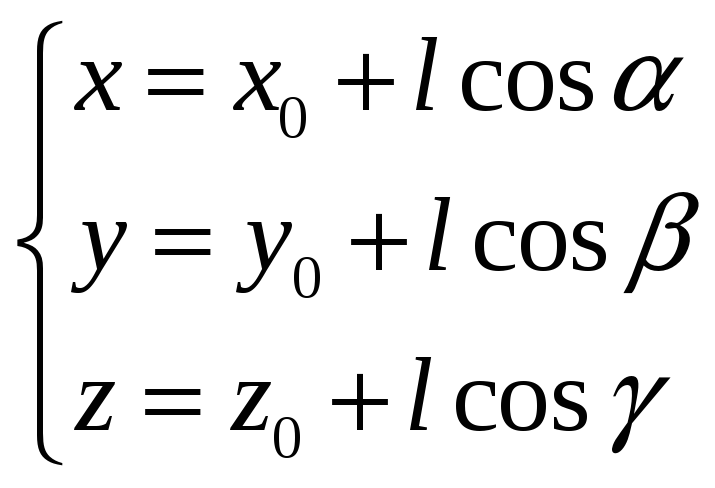
и рассмотрим сложную функцию одной переменной l .

Определение. Производную указанной сложной функции по переменной l, взятой в точке l=0, называют производной функции u=f(x,y,z) в точке M₀(x₀,y₀,z₀) по направлению вектора , и обозначают символом .

Согласно теореме 4, . (5)

Определение. Градиентом функции u=f(x,y,z) в точке M₀(x₀,y₀,z₀) называют вектор с координатами . Вектор градиент обозначают символом grad u.

Итак, . Тогда производная по направлению является скалярным произведением вектора и вектора : . Так как , где φ – угол между векторами и , а , то . Тогда максимальное значение получается при , то есть при совпадении направления с направлением , причем в этом направлении .

Итак, мы доказали два утверждения:

1. производная функции u=f(x,y,z) в точке (x₀,y₀,z₀) по направлению, определенному градиентом этой функции в указанной точке, имеет максимальное значение по сравнению с производной в этой точке по любому другому направлению;

2. значение производной по направлению, определенному градиентом этой функции в данной точке, равно 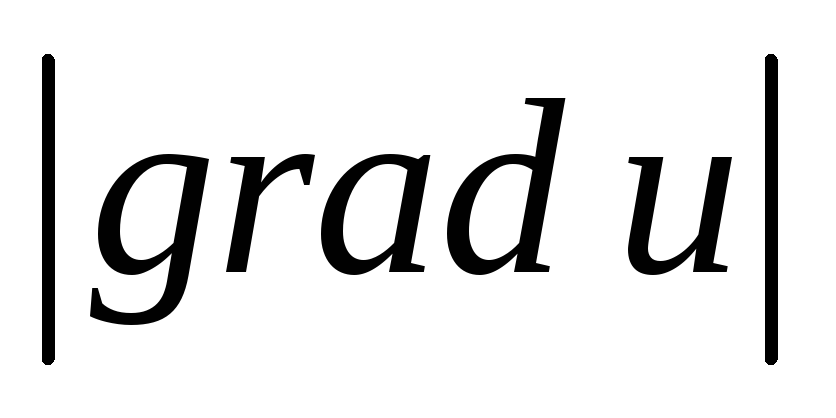, то есть длине вектора в данной точке.

Для выполнения геометрического смысла вектора введем понятие поверхностей уровня функции u=f(x,y,z). Множество точек, удовлетворяющих уравнению f(x,y,z)=c=const, называется поверхностью уровня.

В каждой точке (x₀,y₀,z₀) поверхности уровня f(x,y,z)=c нормальным вектором к касательной плоскости будет являться вектор , другими словами, вектор ортогонален к поверхности уровня.

Аналогичные выводы можно сделать относительно производной по направлению и вектора для функции m переменных, в частности для функции двух переменных.

Задание. Провести выкладки самостоятельно.

Частные производные и дифференциалы высших порядков