8. Дифференциалы высших порядков

Чтобы дать определение дифференциалов высших порядков, введем еще одно обозначение первого дифференциала функции u=f(x₁,x₂,…,x_m) . То есть мы заменили на соответственно. В прежних обозначениях .

Правая часть равенства есть функция переменных x₁,x₂,…,x_m; и если функция f 2-дифференцируема в точке M(x₁,…,x_m), то можно рассмотреть её дифференциал .

Определение. Значение дифференциала от первого дифференциала, взятое при , называется вторым дифференциалом функции f (в данной точке М) и обозначается символом .

Итак, .

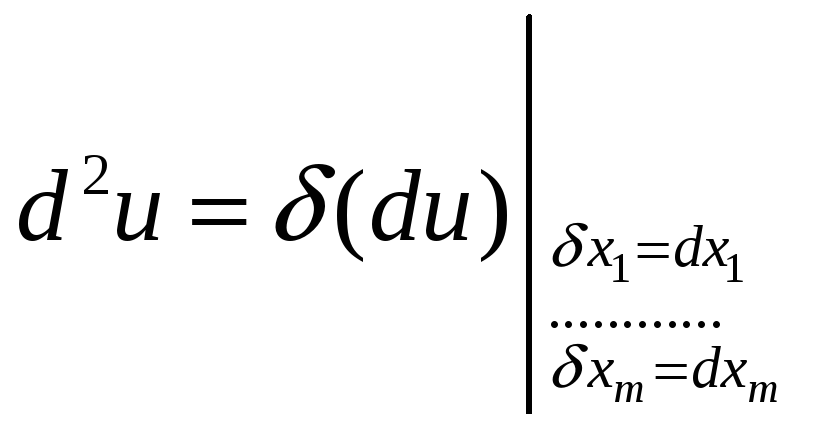Дифференциал dⁿu любого порядка n введем по индукции.

Предположим, что определен дифференциал d^n-1u порядка n-1 и функция f n-дифференцируема в точке M(x₁,…,x_m), а её аргументы x₁,…,x_m являются либо независимыми переменными, либо n-дифференцируемыми функциями некоторых независимых переменных t₁,…,t_k.

.

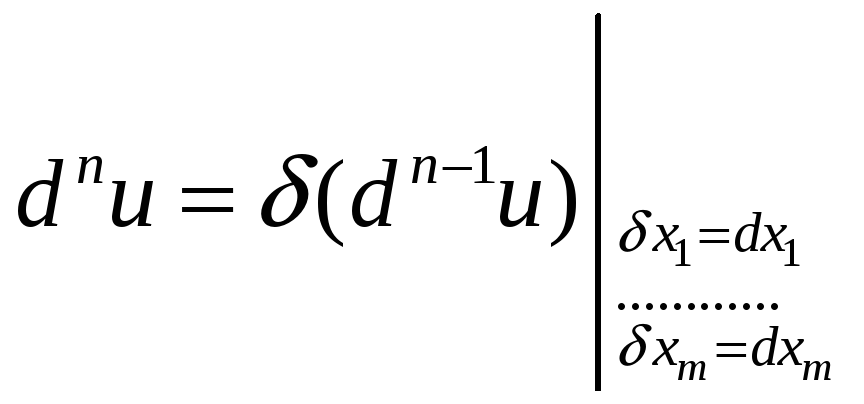При вычислении второго и последующих дифференциалов приходится различать два случая.

1. Пусть аргументы x₁,…,x_m являются независимыми переменными. Тогда 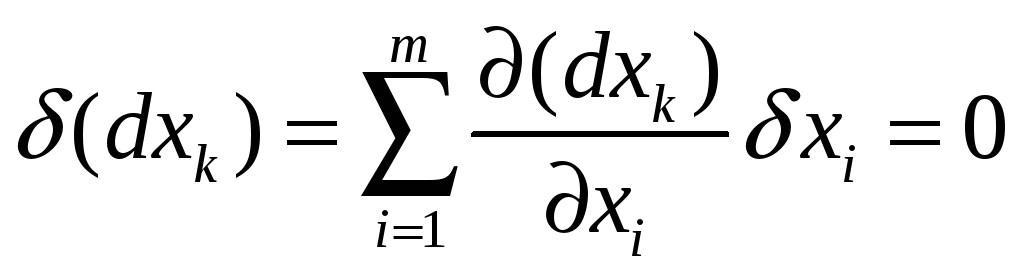, так как 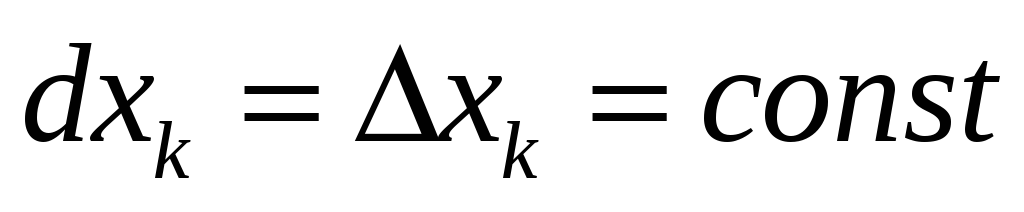для всех точек M(x₁,…,x_m).

Следовательно,

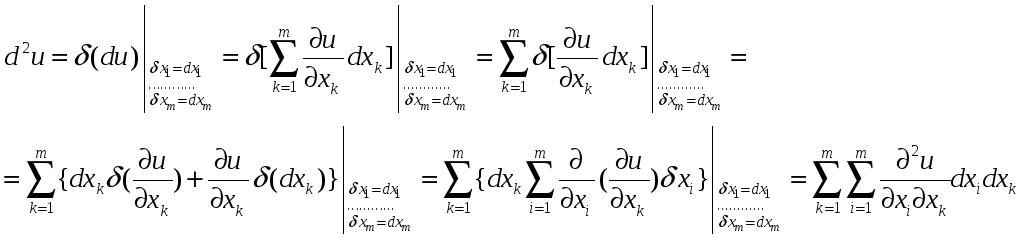
(Мы воспользовались еще и тем, что смешанные производные 2-го порядка не зависят от порядка дифференцирования).

И далее по индукции .

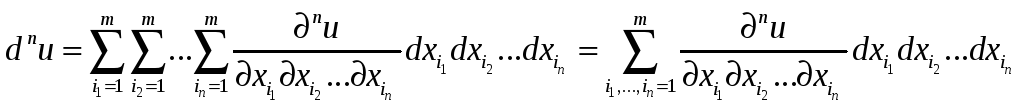Введем формальный символ . Тогда можно записать и (*)

2. Пусть аргументы x₁,…,x_m являются 2-дифференцируемыми функциями некоторых независимых переменных t₁,…,t_k. Тогда

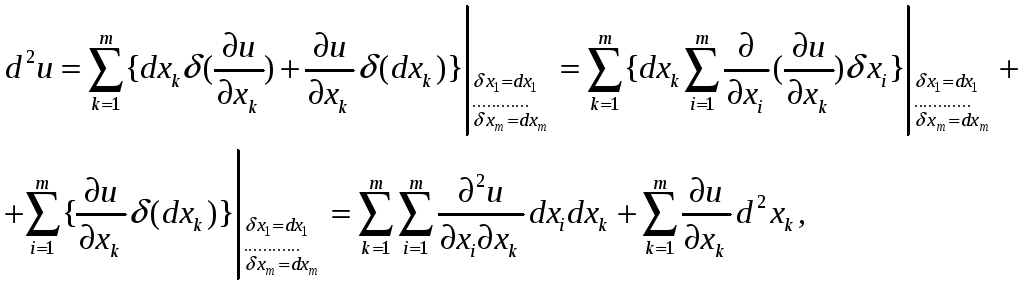
Или (**)

Сравнивая формулы (*) и (**), делаем вывод, что второй дифференциал уже не обладает свойством инвариантности формы. Тем более не обладают этим свойством все последующие дифференциалы.

Замечание. Укажем важный частный случай, когда 2-дифференциал и последующие дифференциалы функции u=f(x₁,x₂,…,x_m) определяются той же самой формулой (*), что и для случая независимых переменных x₁,x₂,…,x_m.

Пусть переменные x₁,x₂,…,x_m являются линейными функциями независимых

переменных t₁,…,t_k: , где - постоянные.

Так как любая частная производная выше первого порядка от линейной функции равна нулю, то . Следовательно, n-дифференциал определяется формулой (*).

9. Формула Тейлора с остаточным членом в форме Лагранжа

Пусть функция u=f(x,y) двух переменных n-дифференцируема в окрестности точки (x,y), и и достаточно малы, чтобы точка принадлежала указанной окрестности.

Тогда и отрезок с концами (x,y) и содержится в ней.

Рассмотрим сложную функцию , определенную на отрезке [0,1] и дифференцируемую на нем (в силу теоремы 4 о дифференцируемости сложной функции).

Имеем: . Далее по индукции получим, что

В аналогичной ситуации для функции u=f(x₁,x₂,…,x_m) имеем: и

Докажем важную теорему.

Теорема 4. Пусть и функция u=f(x₁,x₂,…,x_m) n-дифференцируема в некоторой окрестности точки , а отрезок содержится в ней. Тогда (2)

где (3)

Равенство (2) называют формулой Тейлора с достаточным членом (3) в интегральной форме.

Доказательство. Рассмотрим функцию . Тогда при в силу формулы Тейлора для функции одной переменной .

Полагая , получим: .

Подставляя в полученное равенство в соответствии с формулой (1) значения

, получаем утверждение теоремы.

Замечание 1. Если остаточный член формулы Тейлора для функции записать в форме Лагранжа, т.е. , где , то мы получим остаточный член формулы (2) в виде (4)

Эту форму, так же как и в случае функции одной переменной, называют формой Лагранжа остаточного члена формулы Тейлора.

Замечание 2. Формулу Тейлора с остаточным членом в форме Лагранжа можно переписать в виде: , где в дифференциале функции f и