7. Частные производные высших порядков

Пусть частная производная функции u=f(x₁,x₂,…,x_m), определенной на области G, существует в каждой точке этой области. Таким образом, представляет собой функцию переменных x₁,…,x_m, также определенную на области G. Если эта функция имеет частную производную по переменной x_k в некоторой точке М области, то указанную частную производную называют частной производной второго порядка функции f в точке М сначала по переменной x_i, а затем по переменной x_k и обозначают одним из следующих символов: . При этом если , то частная производная .

Предположим, что уже введено понятие (n-1)-ой частной производной 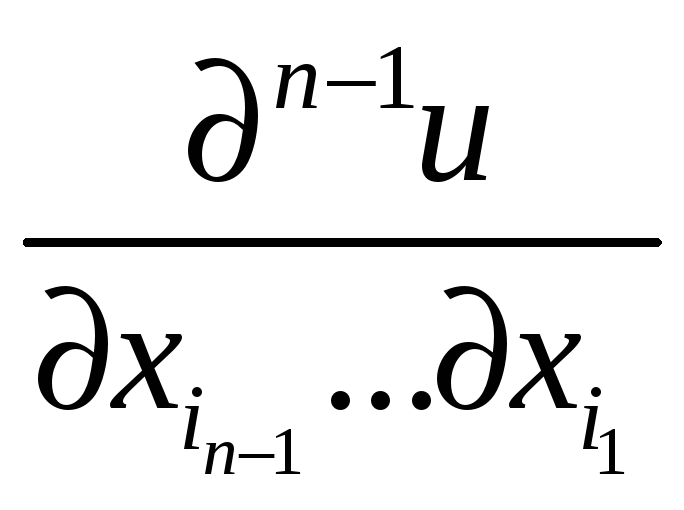. Тогда если эта (n-1)-я частная производная имеет в точке М частную производную по переменной , то указанную частную производную называют n-й частной производной функции f в точке М, т.е. .

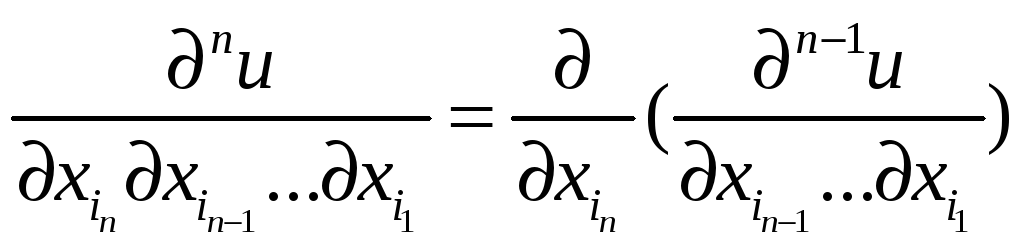Если не все индексы совпадают между собой, то эта частная производная называется смешанной.

Таким образом, мы ввели понятие n-й частной производной индуктивно.

Далее мы выясним достаточные условия независимости смешанных производных от порядка дифференцирования.

Сначала введем важное понятие.

Определение. Пусть n=2,3,… Назовем функцию n-дифференцируемой в точке , если эта функция (n-1)-дифференцируема всюду в некоторой окрестности точки и все её частные производные порядка (n-1) являются дифференцируемыми в точке функциями.

Заметим, что при этом для любого k, удовлетворяющего условию , любая её частная производная порядка k будет (n-k) дифференцируемой в этой точке. Принято также считать функцию 0-дифференцируемой в точке, если она непрерывна в этой точке.

Для того, чтобы функция f была n-дифференцируема в точке достаточно, чтобы все её частные производные n-ого порядка существовали в окрестности точки и являлись непрерывными в этой точке функциями.

Справедливость этого утверждения вытекает из определения n-дифференцируемости и теоремы 3 о достаточных условиях дифференцируемости.

Теорема 1. Пусть функция u=f(x,y) 2-дифференцируема в точке M₀(x₀,y₀). Тогда в этой точке частные производные и равны.

Доказательство. Так как функция f 2-дифференцируема в точке M₀(x₀,y₀), то частные производные и определены в некоторой -окрестности точки M₀ и дифференцируемы в этой точке.

Рассмотрим выражение , где h достаточно мало, так что точка M₀(x₀+h,y₀+h) находится в указанной -окрестности точки M₀. Выражение Ф можно рассматривать как приращение дифференцируемой на отрезке функции одной переменной x. Поэтому по формуле Лагранжа найдется такое, что, Так как дифференцируема в точке M₀, то 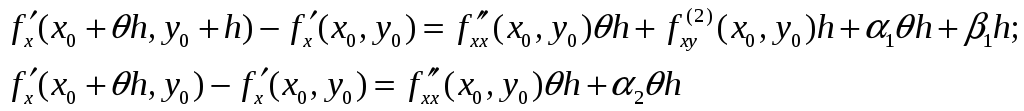, где - бесконечно малые при функции. Тогда , где - бесконечно малая при функция.

С другой стороны, рассматривая как приращение , аналогично предыдущему получим выражение для Ф: , где - бесконечно малая при функция. Тогда . Перейдя к пределу при , получим . Теорема доказана.

Докажем еще одну теорему о равенстве смешанных производных.

Теорема 2. Пусть в некоторой окрестности точки M0(x0,y0) функция f имеет частные производные и производные и непрерывны в точке M0. Тогда .

Доказательство. Воспользуемся выражением Ф из доказательства предыдущей теоремы . Применяя к этой разности формулу Лагранжа по переменной y на отрезке [y₀,y₀+h], получим: , где . В силу непрерывности в точке M₀(x₀,y₀) получим , где при . Следовательно, , и перейдя к пределу при , получим . Теорема доказана.

Докажем теперь теорему о независимости значения любой смешанной производной от порядка дифференцирования.

Теорема 3. Пусть функция u=f(x1,x2,…,xm) n-дифференцируема в точке . Тогда в этой точке значение любой смешанной производной n-ого порядка не зависит от порядка дифференцирования.

Доказательство. Очевидно.

Достаточно доказать равенство .

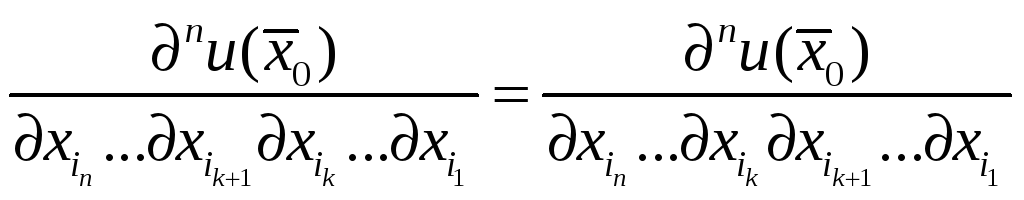Рассмотрим функцию как функцию двух переменных и . Тогда в силу теоремы 1 . Остальное очевидно. Теорема доказана.

Отметим, что любую частную производную n-го порядка можно записать в виде , где - целые числа, удовлетворяющие условиям: .