
- •§1.Общая характеристика атомов.
- •§2.Законы теплового излучения.
- •§3.Испускание и поглощение излучения по квантовой теории. Вывод формулы Планка по Энштейну., 1916г.
- •§5. Ядерная модель атома. Формула резерфорда.
- •§14. Дифракция рентгеновских лучей (рл) на кристаллической решетке.
- •§15. Формула Вульфа-Брегга.
- •§16. Экспериментальное наблюдение дифракции
- •§17. Корпускулярно волновой дуализм.
- •§18. Эффект Комптона.
- •§19. Волновые свойства частиц.
- •§20. Экспериментальное подтверждение гипотезы де Бройля.
- •§21. Статистическая интерпретация волн де Бройля.
- •§22. Соотношение неопределенностей Гейзенберга 1927г.
- •§23. Постулаты квантовой физики.
- •§24. Принцип суперпозиции квантовых состояний.
- •§25. Примеры движения квантовой частицы в стационарных
- •§26. Момент импульса квантовой теории.
- •§27. Гипотеза Уленбека (Юленбека) и Гаудсмита о спине электрона.
- •§28. Спектр атома водорода.
- •§29. Щелочные металлы.
- •§36. Эффект Зеемана.
- •§37. Неразличимость тождественных квантовых частиц.
- •§ 38. Периодическая система элементов (псэ)
§27. Гипотеза Уленбека (Юленбека) и Гаудсмита о спине электрона.
Опыты Штерна и Герлаха.
Предпосылкой гипотезы о спине являлись следующие факты:
Наблюдения Штерна и Герлаха
Магнитомеханические опыты Энштейна, де Гааза, Барнетта, в которых было установлено в два раза большее значение гиромагнитного отношения.

Дублетная структура термов щелочных металлов.
Уленбек
и Гаудсмит предположили, что у электрона
есть не только орбитальный механический
момент
 и соответствующий ему магнитный
орбитальный момент
и соответствующий ему магнитный
орбитальный момент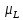 , но и собственный (внутренний) механический
момент
, но и собственный (внутренний) механический
момент , называемый спином, и соответствующий
ему спиновый магнитный момент
, называемый спином, и соответствующий
ему спиновый магнитный момент .
.
Спин – квантовая характеристика, не имеющая классических аналогов и являющаяся внутренним свойством квантовых объектов, характеризующая их равноправно с такими величинами, как масса или электрический заряд.
С точки зрения теоретической физики спин – это дополнительная степень свободы квантовой частицы.

 -
спин, собственный механический момент
-
спин, собственный механический момент
 -
спиновое квантовое число, характеризующее
ту или иную частицу
-
спиновое квантовое число, характеризующее
ту или иную частицу

Спин в отличии от орбитального механического момента строго фиксирован для данной частицы и принимает единственное значение.

Но его проекция также, как и орбитального момента – квантуется.

 -
магнитное спиновое квантовое число
-
магнитное спиновое квантовое число
Гиромагнитное отношение для спиновых моментов:


Говорят, что спиновый момент обладает удвоенным магнетизмом, этот факт – одно из доказательств того, что спин нельзя представить, как вращение частицы относительно собственного диаметра.
 -
проекция магнитного спинового момента
квантуется и у электрона может принимать
два значения:
-
проекция магнитного спинового момента
квантуется и у электрона может принимать
два значения:


Т.о. магнитный момент атома складывается из трех составляющих:

 -
магнитные моменты орбитальной оболочки
-
магнитные моменты орбитальной оболочки
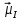 -
магнитный момент ядра. В атомной физике
обычно не учитывается ввиду малости по
сравнению с магнитными моментами
электронной оболочки.
-
магнитный момент ядра. В атомной физике
обычно не учитывается ввиду малости по
сравнению с магнитными моментами
электронной оболочки.
Опыты Штерна и Герлаха доказали существование у атомов магнитных моментов, явление их квантования, а также существование спина электрона.
Схема эксперимента Штерна и Герлаха.

Серебро
было выбрано, т.к. у него один валентный
электрон. Между пластинами создавалось
магнитное поле
 , сильно неоднородное на атомных
расстояниях
, сильно неоднородное на атомных
расстояниях
Было установлено, что пучек атомов серебра расщеплялся относительно начального направления на два симметричных пучка, это расщепление связано с взаимодействием магнитных моментов атомов и приложенного магнитного поля.
Дополнительная энергия, приобретаемая атомом в магнитном поле:
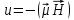

Если бы проекция момента не квантовалась, то в силу неравенства:

мы бы наблюдали на экране сплошную полосу. В действительности на экране наблюдались отдельные пятна. Т.о. было доказано явление квантования магнитных и механических моментов.
Покажем, что из опыта Штерна и Герлаха следует существование спина у электрона.


Предположим,
что
 ,
тогда
,
тогда ,
тогда:
,
тогда:


Всего
 значений
значений при любых
при любых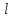 нечетное, т.е. пучок должен разбиваться
на 1, 3, 5, …
нечетное, т.е. пучок должен разбиваться
на 1, 3, 5, …
Для объяснения четного количества компонент на экране рассмотрим атом серебра с одним валентным электроном на внешней оболочке.

Для
атома серебра в основном состоянии
орбитальное квантовое число
 .
Тогда
.
Тогда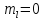 ,
,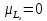 .
В данном случае магнитный момент чисто
спиновый.
.
В данном случае магнитный момент чисто
спиновый.
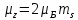
Т.к.
для одного электрона на внешней оболочке
возможно всего две проекции
 спинового момента, то весь пучок
разбивается на две компоненты.
спинового момента, то весь пучок
разбивается на две компоненты.
Глава: Теория атомов и молекул.
