§21. Статистическая интерпретация волн де Бройля.

Рассмотрим схему по интерференции света, предложенную Юнгом.

Аналогичную схему по интерференции имели опыты Бибермана, Фабриканта, Сушкина (1949).

- характерное время, необходимое электрону для преодоления интерферометра.

Опыты проводились в двух режимах:

1. Электроны запускались по одному: . Т.о., исключалась возможность взаимодействия электронов между собой и влияния этого взаимодействия на интерференционную картину. Опыт повторялся многократно с длительным временем экспозиции (эксперимента).

2. Электроны запускаются потоком с малым временем экспозиции.

Результаты эксперимента оказались одинаковыми в том и другом случае, при этом весьма парадоксальными. Если закрыть одну из щелей, то на экране будет один из максимумов. Теоретически, для двух щелей ожидалось увидеть картину двух максимумов:

На опыте была зарегистрирована картина, аналогичная интерференции света:

Если считать, что электрон проходит через какую-то одну щель, то наличие интерференционной картины наводит на мысль, что электрон каким-то образом ощущает вторую щель, иначе ему было бы безразлично состояние второй щели, и в этом случае наблюдалась бы корпускулярная сумма интенсивностей.

Т.о., на характер интерференционной картины, а значит и на движение электрона влияют обе щели! Этот вывод несовместим с классическими представлениями о том, что электрон движется по какой-то траектории (если бы это было так, то электрон двигался бы только через одну определенную щель, однако электрон не можем одновременно проходить через две щели, т.к. это элементарная частица, которую невозможно расщепить).

Вывод: микрочастицу нельзя представлять, как классическую м.т., движущуюся по определенной траектории.

В случае опыта с регистрирующими электроны устройствами возле каждой щели было установлено, что всегда срабатывает счетчик только одной щели, т.е. электрон действительно не расщепляется. Однако в этом опыте электрон начинает вести себя, как корпускула и интерференционная картина не наблюдается.

Вывод: наблюдение за микрочастице изменяет ее состояние.

Наблюдение интерференции и дифракции электронов позволило М.Борну в 1926г. Предложить статистическую интерпретацию волн де Бройля, которая сочетает анатомизм (неделимость) и волновые свойства, связанные с тем, что волны де Бройля следует рассматривать, как волны вероятности.

Интенсивность волны де Бройля в какой-либо точке пространства пропорциональна вероятности обнаружить частицу в данной точке.

Статистика микрочастиц не зависит от их количества и одинакова, как для одиночных частиц, так и для их потоков.

Поясним появление интерференции. Перед попаданием в интерферометр все электроны проходят одинаковую разность потенциалов, а значит имеют одну и ту же длину волны λ де Бройля. В какую точку экрана попадает электрон, достоверно предсказать не возможно, но вероятность этого попадания пропорциональна интенсивности волны де Бройля в этой точке, значит электрон, в основном, будет попадать в те точки экрана, для которых выполняется условие максимума.

Из оптики известно:

Рассмотрим движение электрона с постоянной скоростью в отсутствии действия внешних сил, при этом состояние электрона описывается уравнением волны де Бройля.

Такой электрон равновероятно обнаружить в любой точке пространства. Волна де Бройля – простейший частный случай некоторой функции состояния микрочастицы.

В квантовой физике для описания состояния микрочастицы вводится некоторая волновая функция 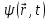, сложным образом зависящая оти. На опыте, волновая функция не наблюдается и сама по себе физического смысла не имеет, хотя ее называют амплитудой вероятности.

Вероятность обнаружения частицы в объеме в окрестности точкив момент времени:

–плотность вероятности, вероятность обнаружения частицу в единичном объеме.

Условие нормировки волновой функции:

Равенство единице вероятности обнаружения частицы в объеме означает достоверность данного события.

Рассмотрим вероятность волны де Бройля.

Данный интеграл расходится, в таком случае выполнение условия нормировки требуют на ограниченной области:

Волновая функция позволяет определить среднее значение физических величин, наблюдаемых в опыте, например среднее значение координаты можно рассчитать следующим образом: