§19. Волновые свойства частиц.

Гипотеза де Бройля (1924г.)

Де Бройль предложил, что частицам вещества также, как и световым квантам, присуще не только корпускулярные, но и волновые свойства. Для частиц выполняется соотношение де Бройля.

Где 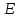и- энергия и импульс частицы, связанные между собой релятивистским соотношением:

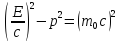
и - частота и длина волны де Бройля.

Постоянная монохроматическая волна де Бройля или волна материи:

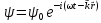
Волну де Бройля можно сопоставить равномерному прямолинейному движению частицы массы со скоростью.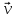

В отсутствии действия внешних сил:

Координатная часть волновой - функции:

Временная часть волново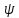й - функции:

–величина, наблюдаемая на опыте.

Волна де Бройля является частным случаем сложного движения, которое в квантовой механике можно описать волновой функцией .

Найдем длину волны, соответствующую частице:

Откуда получаем длину волны де Бройля:

1. Рассмотрим пример камня массой , летящего со скоростью:

- атомная физика.

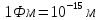- ядерная физика.

Зарегистрировать волновые свойства макрообъектов на данный момент невозможно.

2. Рассмотрим электрон, ускоренный разностью потенциалов :

При разности потенциалов 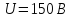длина волны, что сопоставимо с длиной волны РИ, а значит можно наблюдать дифракцию электронов теми же методами, что и в рентгеноструктурном анализе и рентгеновской спектроскопии.

Свойства волн де Бройля.

Рассмотрим фазовую скорость волн де Бройля - скорость перемещения поверхности равных фаз.

и - полные энергия и импульс частицы.

Данное уравнение не противоречит СТО, т.к. с фазовой скоростью не связан не перенос энергии, не перенос массы, за перенос энергии и массы отвечает групповая скорость.

Рассмотрим волновой пакет с очень близкими частотами. Групповая скорость волнового пакета – скорость перемещения максимальной по амплитуде составляющей.

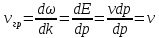
Групповая скорость волнового пакета совпадает со скоростью движения частицы.

§20. Экспериментальное подтверждение гипотезы де Бройля.

1. Опыт Девиссона и Джернера (по сути: дифракция электронов по схеме Вульфа-Брегга).

Электронная пушка позволяла получать монохроматические электроны с длиной волны де Бройля.

Коллектор улавливает дифрагировавшие от кристалла электроны.

Опыт состоял из двух частей:

1. Регистрировался ток дифрагировавших электронов в зависимости от угла скольжения при постоянной длине волны де Бройля

Полярная диаграмма, в которой длина отрезка от начала координат до точки , проведенного под углом , соответствует регистрирующему току.

Было установлено, что дифракционный максимум наблюдается при угле падения равном углу отражения.

Дифракционные условия Вульфа-Брегга:

- порядок максимума.

По известному значению и параметру решеткиможно рассчитать угол, под которым наблюдается тот или иной дифракционный максимум.

В опыте Девиссона-Джернера была установлена справедливость соотношения Вульфа-Брегга для электронов.

2. Регистрировалась зависимость при постоянном угле скольжения

Максимум силы тока соответствует условию максимумов интерференционного отражения.

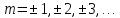
Отсюда следует, что расстояние между соседними максимумами должно быть постоянным, что и соответствует опыту.

2. Дифракцию электрона можно наблюдать методом Лауэ.

Для генерации белого (сплошного) спектра напряжение на электронной пушке должно непрерывно изменяться, т.к.

3. Томсон и Тартаковский в опыте по дифракции электронов использовали метод Дебая

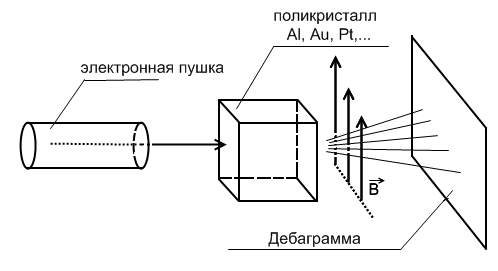
Для того, чтобы убедиться, что дифракционная картина образована электронами, а не вторичным РИ, в промежутке между поликристаллом и экраном создавалось МП, которое смещало электроны и вызывало сдвиг дифракционной картины.

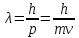
Волновые свойства атомов и молекул наблюдать значительно сложнее, чем электрона, тем не менее принципиально возможно.

В дальнейших опытах было установлено, что волновые свойства присущи не только потоку частиц, но и каждой отдельно взятой.