§36. Эффект Зеемана.

Эффект Зеемана состоит в расщеплении спектральных термов и соответствующих спектральных линий в МП.

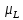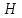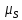В слабом МП - связь сохраняется, т.е. взаимодействиеимежду собой сильнее, чем взаимодействие отдельных моментови,ис МП. В таком случае наблюдается аномальный эффект Зеемана, при котором спектральные линии расщепляются больше, чем на три компоненты.

В сильном МП спин – орбитальное взаимодействие разрывается, т.к. энергия взаимодействия отдельных моментов с МП превосходит энергию спин – орбитального взаимодействия 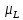и.

В МП любой уровень расщепляется на 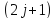компонент, которые расположены на одинаковом расстоянии друг от друга, это расщепление много меньше, чем расстояние между компонентами тонкой структуры.

Рассмотрим пример главной серии щелочных металлов:

Любой переход данной серии имеет две компоненты тонкой структуры.

Рассмотрим терм :

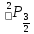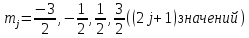
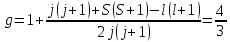
Рассмотрим терм :

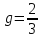
Рассмотрим терм :

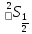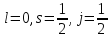
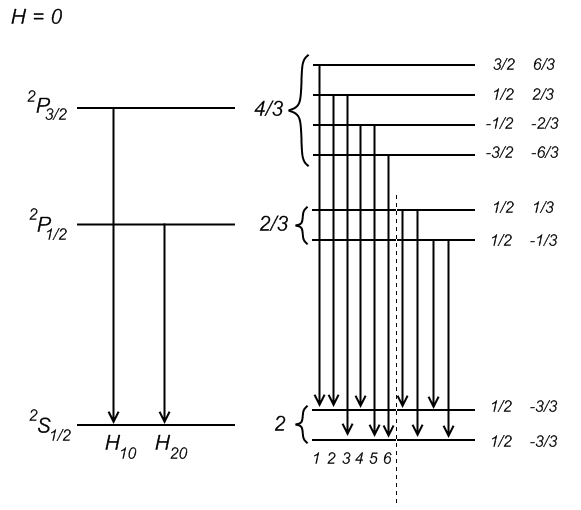
Правила отбора в слабом МП:

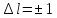
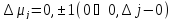
Рассмотрим частоты перехода :

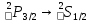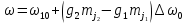
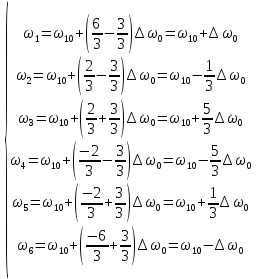
Спектральные линии при этом расщепляются на три компоненты. Этот эффект называют эффектом Пашена – Бака.

Для термов в слабом МП также наблюдается ращепление на три компоненты. Этот эффект называют нормальным эффектом Зеемана длятермов.

В МП сохраняется только проекция механического момента на выделенное направление.

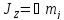
В общем случае в МП энергия атома зависит от трех квантовых чисел: главного квантового числа, орбитального квантового числа, спинового квантового числа.

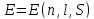
В МП энергия атома оказывается зависящей от дополнительного квантового числа .

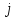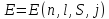
Таким образом, в МП один энергитический уровень атома расщепляется на 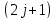Зеемановский подуровень.

Значит, 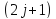- есть статистический вес уровня или кратность его вырождения в отсутствии МП.

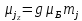
Атом в МП обладает дополнительной энергией, которая определяется, как:

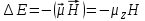
1. Аномальный эффект Зеемана.

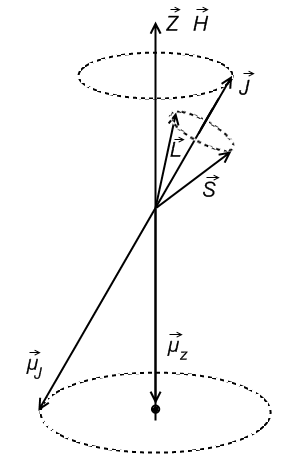
Для случая 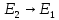с испусканием света в отсутствии МП:

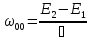
В присутствии МП энергия атома:

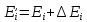
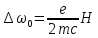
–Лоренцева частота или частота нормального расщепления спектральной линии.

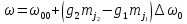
Д/З: рассчитать частоты переходов, соответствующих второй компоненте .

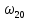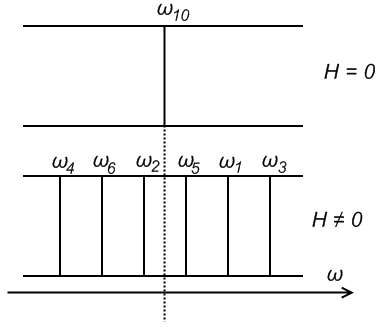
2. Нормальный эффект Зеемана.

Расщепление спектральных линий, соответствующих синглетным уровням, на три компоненты. Лоренцев триплет.

Для синглетных уровней:

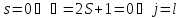
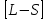–связь отсутствует.

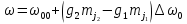
Согласно правилам отбора

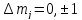
Лоренцев триплет:

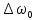- частота нормального расщепления.

Можно считать, что для синглетных уровней любое магнитное поле сильное, т.к. оно взаимодействует только с магнитным орбитальным моментом.

3. Расщепление спектральных линий в сильном МП. Эффект Пашена – Бакка.

В сильном МП - связь разрывается и поле взаимодействует по отдельности с орбитальным и спиновым магнитным моментами.

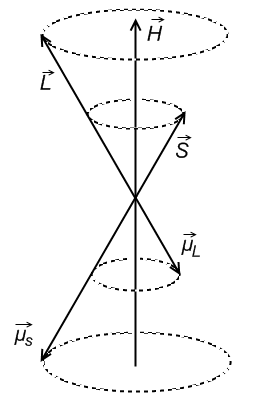
Результирующий магнитный момент атома:

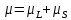
Дополнительная энергия, приобретенная атомом:

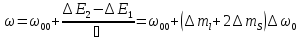
Правила отбора в сильном МП:

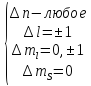
Т.о., в сильном МП каждая компонента расщепляется на три.

Расщепление спектральных линий в ЭП называют эффектом Штарка.

§37. Неразличимость тождественных квантовых частиц.

Принцип Паули (пятое начало квантовой механики).

Рассмотрим СС одинаковых квантовых частиц, например электронов. Все они имеют одинаковые характеристики: 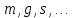, однако в отличии от классических частиц, все эти электроны принципиально не различимы. Если классическим частицам можно сопоставить определенную траекторию, другими словами - пронумеровать, то для квантовых частиц это невозможно в силу соотношений неопределенности.

Вероятность нахождения СС в таком состоянии, что:

В элементе объема :

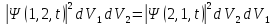
Т.к. частицы принципиально не различимы, это равенство возможно в двух случаях:

1) – волновая функция симметрична относительно перестановки двух частиц.

2) 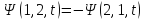– волновая функция антисимметрична.

Общая формулировка принципа Паули:

Волновая функция СС тождественных частиц с полуцелым спином полностью антисимметрична относительно перестановки двух частиц. Частицы с полуцелым спином называются фермионами и говорят, что они подчиняются статистике Ферми – Дирака.

Волновая функция тождественных частиц с целым спином полностью симметрична относительно любых перестановок частиц, сами такие частицы называют бозонами и говорят, что они относятся к статистике Бозе – Энштейна.

Для фотона:

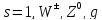
Рассмотрим атом, как многоэлектронную СС, будем считать, что взаимодействие электронов между собой незначительно. Тогда состояние любого электрона в атоме описывается четырьмя степенями свободы, другими словами, четырьмя квантовыми числами, эти четверки могут быть выбраны любыми:

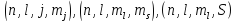
Рассмотрим наиболее общий случай :

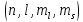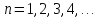1. - главное квантовое число

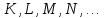- обозначение квантового слоя

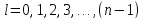2. - орбитальное квантовое число

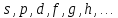
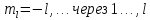3. - магнитное орбитальное квантовое число

способом орбитальный момент импульса может ориентироваться относительно выбранного направления.

4. – магнитное спиновое квантовое число

способом спиновый механический момент может ориентироваться на выделенное направление.

Частная формулировка принципа Паули:

В атоме не может быть двух или более электронов с одинаковой четверкой квантовых чисел.

Рассмотрим основное триплетное состояние атома гелия. Докажем, что для него невозможно состояние:

1. 

2. 

Из вышестоящего следует, что . Значит, гелий может находиться только в основном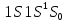синглетном состоянии, а состояние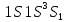- запрещено принципом Паули, т.к. для его реализации необходимо противоречащее принципу Паули равенство всех четырех квантовых чисел.

Очевидно, что терм 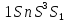, где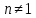возможен:

1. С одинаковыми квантовыми числами 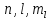. В атоме может быть только два электрона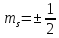

2. С одинаковыми квантовыми квантовыми числами 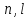в атоме может быть толькоэлектрона.

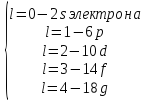
3. С одним и тем же квантовым числом в атоме может бытьэлектронов.

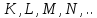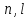Электроны с одинаковым значением образуют электронную оболочку атомаОболочки электронов с одинаковыми числаминазывают эквивалентными, они образуют подоболочку атома