telnov-mechanika-and-TO

Здесь Vr′ – это скалярное произведение.

Пример. Пусть два события произошли одновременно в системе S ′ в различных точках x1′ и x2′. Из формул обратного преобразования

Лоренца получаем временной интервал между этими событиями в системе S

Именно поэтому при измерении длины линейки, лежащей вдоль движения в системе S ′ , экспериментаторы из систем S и S ′ получают разные результаты.

Наконец, рассмотрим пример, позволяющий до конца понять, почему в приведенном в предыдущем разделе примере при одновременном ускорении в лабораторной системе двух зарядов расстояние в сопутствующей системе возрастает. Пусть эти два заряда, расположен-

ные на расстоянии l0 , одновременно (в лаб. системе S ) в результате

удара получают скорость V . В сопутствующей системе расстояние между ними будет в γ раз больше. Как это могло произойти?!

Очень «просто». Рассмотрим, как произошли эти удары в системе отсчета S ′ , движущейся со скоростью V , в которой эти заряды после ударов будут покоиться. Во-первых, в этой системе удары произошли не одновременно. Действительно, в лабораторной системе

x1 = 0, x2 = l0, t1 = t2 = 0 , тогда из преобразований Лоренца для вре-

мени (18.5), t′ = γ(t −Vxc2 ), находим, что в движущейся системе эти

времени второй заряд еще покоился в лаб. системе, т.е. двигался назад

41

это как раз то, что мы и хотели объяснить! Увеличение расстояния происходит из-за того, что системе S ′ имеется задержка между ударами.

Формулы (18.6) получены в 1904 году Х. Лоренцем как преобразования, при которых уравнения электродинамики сохраняют свой вид при переходе от одной инерциальной системы к другой. В 1905 году А.Эйнштейн вывел их из постулатов о равноправии всех инерциальных систем и существовании максимальной скорости передачи сигналов. Хотя получились те же самые преобразования, но физическое содержание в них было совершено новым.

Интересно, что Эйнштейн неоднократно выдвигали на Нобелевскую премию за разработку специальной теории относительности, но ее не давали (дали позже за объяснение фотоэффекта, гипотезу о фотонах). Причина состояла в том, что Лоренц был против, т.к. он раньше нашел закон преобразования. Сам же Х. Лоренц получил Нобелевскую премию в 1902 г за другие работы.

§ 19. Четырехмерный вектор события.

Упорядоченную четвёрку чисел R = (ct,x,y,z) ≡ R(ct, r) называют

4-вектором события. В отличие от обычного вектора, обозначаемого стрелкой или жирной буквой, 4-вектор пишут обычным шрифтом.

Обычно знак суммирования опускают, подразумевая, что происходит суммирование по повторяющемуся индексу. Аналогично можно

записать R = L−1R′, где L−1 - матрица обратного преобразования, отличающаяся от L заменой β на −β. Запись в матричной форме здесь

приведена чисто для красоты (матрицы широко используются в теоре-

42

метрию, в отличие от евклидовой, называют псевдоевклидовой. Она была введена в теорию относительности Г. Минковским, и данное пространство называют пространством Минковского

Выше мы видим, что если интервал равен нулю в одной системе отсчета, то он равен нулю и в любой другой системе отсчета. А как связаны между собой интервалы s и s′ в общем случае? Оказывается, они всегда равны! В этом легко убедиться, выразив в (20.3) x,y, z,t че-

рез x′,y′, z′,t′, используя преобразования Лоренца. Действительно, поскольку поперечные координаты сохраняются, y = y′ и z = z′, то ос-

Подставляя (20.5) в правую часть (20.4), после небольших преобразований находим, что правая часть тождественно равна левой. Таким образом, мы убедились, что

Это замечательный результат! В классической механике, где верны преобразования Галилея, инвариантом преобразования является длина отрезка

Инвариантность интервала при релятивистских скоростях можно доказать формально, не прибегая к преобразованиям Лоренца. Рассмотрим два близких события, имеющие интервал

ds2 = c2dt2 − dx2 − dy2 − dz2 .

Выше было показано, что, если ds = 0 , то и ds′ = 0 . В общем случае для ds ≠ 0 следует ожидать

ds12 = a(V )ds122 ,

где коэффициент a может зависеть только от абсолютной величины относительной скорости. Он не может зависеть от координат и времени, так как тогда различные точки пространства и моменты времени

44

были бы неравноценны, что противоречит однородности пространства и времени. Он не может зависеть также и от направления относительной скорости, так как это противоречило бы изотропии пространства. Рассмотрим три системы отсчета S, S1, S2 и пусть V1 и V2 — скорости

движения систем S1 и S2 относительно S . Тогда имеем:

С тем же основанием можно написать ds12 = a(V12 )ds22

где V12 — абсолютная величина скорости движения S1 относительно S2 . Сравнивая друг с другом эти соотношения, найдем, что должно быть

a(V ) =

a(V2) a(V12 )

1

Но V12 зависит не только от абсолютных величин векторов V1 и V2 ,

но и от угла между ними. Между тем угол вообще не входит в левую часть соотношения. Ясно поэтому, что это соотношение может быть справедливым лишь, если функция a(V) сводится к постоянной величине, равной, как это следует из того же соотношения, единице. Таким образом,

ds12 = ds22 .

Из равенства бесконечно малых следует, что и s1 = s2 .

§ 21. Преобразований Лоренца как вращение в четырехмерном пространстве

Ранее мы вывели преобразования Лоренца, пользуясь очень наглядной и физической картиной, основанной на постоянстве скорости света во всех инерциальных системах отсчета. Теперь рассмотрим другой, менее прозрачный, но более короткий вывод преобразования Лоренца. Преобразование координат и времени при переходе в другую систему отсчета должно быть таким, чтобы сохранялась неизменной величина интервала в четырехмерном пространстве. Такими переходами из одной инерциальной системы в другую являются параллельные переносы и вращения системы координат. Однако переносы системы координат не представляют интереса, т.к. сводятся к переносу начала

45

отсчета координат и времени. Таким образом, искомое преобразование должно быть связано с поворотом осей координат.

Введем обозначение T = ict , где i = −1 - мнимая единица. Тогда все 4 координаты становятся равноценными и можно пользоваться евклидовой геометрией. Рассмотрим поворот осей в плоскости T, x, y и z при этом не изменяются. Из геометрических соображений нетрудно получить, что при повороте осей на угол ϕ координаты точки преоб-

разуются следующим образом

Пусть вас не удивляет, что tgϕ – мнимое число, это ведь отношение

двух "катетов", один из которых мнимый. Подставляя (21.4) в (21.1) получаем снова преобразования Лоренца

46

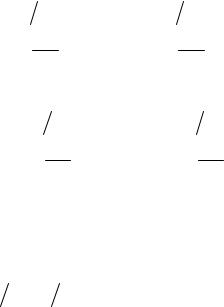
§ 22. Преобразование скоростей

Пусть некоторое тело движется относительно системы отсчёта S ′ со скоростью v′ . В свою очередь S ′ движется относительно S со скоростьюV вдоль оси OX . В кинематике Галилея скорость тела относительно S есть просто векторная сумма переносной скорости V и от-

В релятивистской кинематике это правило сложения скоростей неверно. Для получения правильных формул продифференцируем преобразования Лоренца

Легко убедиться, что при малых скоростях эти формулы переходят в правило Галилея для преобразования скоростей.

Пример. Если ракета летит со скоростью V ≈ c и выпускают вперед снаряд со скоростью vx′ = c , то скорость снаряда относительно неподвижного наблюдателя будет равна

§ 23. Аберрация

Пусть в системе S ′ движется тело со скоростью v′ под углом θ к оси OX ′. Найдем, под каким углом к оси X это тело движется в системе S, рис. 22.

47

В случае если тело движется с предельной скоростью v′ = c , например свет, можно легко получить выражения для sin θ и cosθ , заме-

тив, что и в системе S скорость света также равна c. Тогда

Этот случай называется световой аберрацией. Обратный переход

Пример. Пусть в космическом корабле произошла вспышка света. Нетрудно получить направления лучей в лабораторной системе:

48

Видим, что свет, испущенный в системе корабля в переднюю полусферу, соберётся в конус sin θ = 1 γ вокруг направления движения

корабля. Это явление называют «эффектом фары».

Явление аберрации искажает картину звёздного неба. Рассмотрим, что увидят наблюдатели в космическом корабле. Воспользуемся формулами (23.4) и учтем, что свет от звёзд падает на корабль, т.е. нужно заменить c на −c . Пусть в лабораторной системе луч света падает на корабль по углом θ к направлению движения. Тогда в системе корабля

Передняя полусфера неба соберется в системе отсчёта корабля в угол

Явление звёздной аберрации впервые наблюдал Брэдли в 1725 году. В результате орбитального движения Земли относительно Солнца, угол, под которым видны звёзды, меняется в течение года на величину

V/c ≈ 10−4 . Пример нерелятивистской аберрации – изменение направления падения капель дождя при движении наблюдателя.

§24. Эффект Доплера

При наблюдении звёздного неба из кабины движущегося космического корабля меняется не только распределение звёзд на небе, но и изменяется их цвет и яркость. Как известно, свет характеризуется частотой, длиной волны и скоростью распространения. Пусть волна возбуждается электронами, движущимися в плоскости XY (т.е. z = 0 ). Волна будет распространяться в направлении Z . Рассмотрим только электрическую компоненту поля. Пусть вблизи поверхности z = 0

E = E0(t) . Тогда поле в точке с координатой z

49

т.е. равно полю у источника с задержкой zc . Пусть E0 = Acos ωt , тогда

где k = ωc . В заданной точке пространства поле меняется с периодом (фаза, ωt −kz , меняется на 2π)

Сдругой стороны, k = ωc , откуда следуют тривиальные

Здесь k – волновой вектор, направленный в сторону распространения волны, его модуль определен (24.4).

Переходим, наконец, к нашей задаче – преобразованию частоты и волнового вектора волны при переходе из одной инерциальной системы отсчёта в другую. Здесь может возникнуть вопрос, зачем нам нужно знать преобразование вектора k ? Во-первых, оказывается, между ω и k имеется глубокая связь – они образуют 4-вектор; во-вторых, для квантов электромагнитного поля, фотонов, энергия и импульс равны E = ω , p = k (это будет обсуждаться подробно в разделе релятиви-

стская динамика).

Итак, представим себе, что источник в системе S ′ создаёт систему плоских волн, распространяющихся из начала координат O′ под углом θ′ и характеризующуюся длиной волны λ′ = λ0 и периодом T ′ =T0

(для простоты считаем, что происходят короткие вспышки через вре-

мя T0 ), рис.23.

50