telnov-mechanika-and-TO

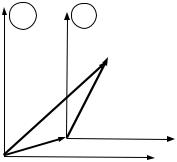
Г Л А В А XI.

ДВИЖЕНИЕ В НЕИНЕРЦИАЛЬНЫХ СИСТЕМАХ ОТСЧЕТА

§ 89. Неинерциальные системы отсчета. Неинерциальные силы.

До сих пор исследовалось движение тел относительно инерциальных систем отсчета, в которых справедливы Законы Ньютона.

Рассмотрим теперь движение тела (материальной точки) относи-

Т.е., если движение рассматривается относительно системы отсчета, ускоренно движущейся относительно инерциальной системы отсчета, то во втором законе Ньютона, кроме реальной силы, появляется до-

полнительное слагаемое -ma0 . Это не реальная, а фиктивная сила, имеющая чисто кинематическое происхождение, пропорциональная

221

массе тел (как и гравитационная сила). Такие силы называют силами инерции. Они появляются в неинерциальных системах отсчета.

Казалось бы, рассматривай все в инерциальных системах, тогда все просто, никаких сил инерции. Это так, но иногда удобно систему координат связывать с ускоренно движущимися телами, такими как вращающаяся Земля или ускоренно движущаяся тележка.

Рассмотрим тележку, движущуюся с ускорением a , на которой стоит подставка с висящим на нитке грузиком, рис.84. На какой угол отклонится грузик?

В инерциальной системе задача рассуждения следующие:

222

§ 90. Силы инерции во вращающейся системе отсчета

Центробежная сила.

Для того, чтобы тело было неподвижно относительно диска, вращающегося с угловой скоростью w , к нему нужно приложить центростремительную силу

Чтобы объяснить неподвижность тела в системе вращающегося диска нужно объявить, что кроме реальной силы (например, натяжение веревки, связывающей тело с осью) в этой системе действует сила инерции

направленная от центра. Ее называют центробежной силой. Эта сила уравновешивает натяжение веревки, и тело остается неподвижным относительно вращающегося диска. Такой силы нет в инерциальной лабораторной системе, ее вводят только при рассмотрении движения во вращающейся системе отсчета.

Кориолисова сила

Рассмотрим движение тела со скоростью v относительно обода вращающегося диска. Для такого движения неподвижной системе координат должна действовать центростремительная сила

Наблюдатель, сидящий на диске, видит, что веревка натянута с таким натяжением, значит в этой системе отсчета натяжение веревки уравновешено силами инерции

Первый член в (90.4) это уже знакомая центробежная сила, третий член

– это обычная центростремительная сила, необходимая для движения по окружности, второй член, F = 2mwv , зависит как от угловой скорости вращения диска, так и от скорости движения тела относительно диска, называется Кориолисовой силой ( Г.Кориолис, 1792-1843).

223

Рассмотрим движение тела вдоль спицы вращающего колеса. Мо-

мент инерции тела L = mwr2 увеличивается при движении от центра. Изменение момента импульса за единицу времени равно моменту сил

Эта сила, с которой спица действует на тело, сопротивляясь силе Кориолиса. Поскольку сила Кориолиса перпендикулярна угловой скорости и скорости тела, то в векторном виде ее можно записать как

Далее мы получим это выражение строго математически.

Рассмотрим снова рис.83. Система S является неподвижной, а система S ¢ движется относительно ее как поступательно, так и вращательно. Скорость материальной точки относительно неподвижной системы

224

находим

центробежное

Рассмотрим смысл каждого члена.

aабс = F / m – это ускорение, вызванное реальной силой;

a0 +[ω× r] +[ω×[ω× r]] – переносное ускорение, связанное с движением системы S ¢ ;

2[ω× vотн ] – ускорение Кориолиса.

Член [[ω× r]×ω] в переносном ускорении – это центробежное ускорение. Полагая r = r + r^ (относительно ω), находим

Перегруппируя члены в (90.14) с учетом (90.15) получим уравнение относительного движения

Примеры силы Кориолиса:

Маятник Фуко – это обычный тяжелый маятник на длинном подвесе. Впервые публичная демонстрация была осуществлена Фуко в 1851 г. в Парижском Пантеоне. Плоскость колебаний

ωтакого маятника поворачивается относительно земной поверхности в сторону, противопо-

225

угловой скорости параллельная поверхности Земли не влияет, т.к. создает силу вдоль троса. Период вращения плоскости колебаний

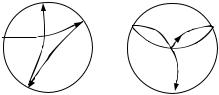
На рис. 87 показаны фигуры, описываемые нижним концом маятника, если его оттянуть и опустить (слева) и толкнуть из центра (справа).

Подмывание берегов

В северном полушарии сила Кориолиса направлена вправо от направления движения, поэтому правые берега рек в Северном полушарии более крутые – их подмывает вода. В Южном полушарии всё происходит наоборот.

Колеса поезда

Правые колеса (в северном полушарии) поезда сильнее прижимаются к рельсу сбоку и быстрее снашивается.

Ураганы

Ураганы закручиваются силой Кориолиса. Наиболее сильные на сороковых «ревущих» широтах. На экваторе не бывает.

§91. Приливы

Уберегов морей и океанов дважды в сутки наблюдается подъем уровня воды до некого максимального значения и столько же раз опускание до минимального уровня. Они являются результатом изменения положений Луны и Солнца относительно Земли совместно с эффектами вращения Земли и особенностями рельефа. В некоторых местах подъем достигает 10-15 м, но в среднем перепад составляет порядка одного метра. Аномальные подъемы связаны с увеличением высоты волны при набегании ее на берег и геометрией береговой линии.

226

C

O

Рис. 88

Рассмотрим механизм возникновения приливной волны в идеализированном случае, когда имеется сплошной океан. Приливные силы зависят не от величины гравитационного поля (Луны, Солнца), а от степени его неоднородности (градиента). Ниже будет получено соотношение приливных эффектов от Луны и Солнца. Пусть для определенности Луна притягивает Землю, рис.88. Рассмотрим ускорения, действующие в точках А, B и С, вычитая при этом ускорение центра масс Земли.

Поскольку точка А ближе у Луне, то в ней дополнительная гравитационная сила направлена к Луне, в то время как в противоположной точке В сила такая же, но направлена от Луны. В точке C имеется составляющая перпендикулярная линии, соединяющей Луну и Землю. Приливы в точках А и В будут происходить одновременно и одинаковой величины.

Ускорение в точке находящейся между О и А на расстоянии x от центра Земли за вычетом ускорения центра Земли равно

Потенциал в точке А относительно О, связанный с этим градиентным полем,

Потенциал между точками С и О может быть найден непосредственно как разность потенциалов в этих точках, поскольку в этом направлении центр масс Земли не имеет ускорения.

227

Отсюда разность эффективная разность потенциалов между А и С (эффективная потому, что вычтено поле, действующее на ц.м. Земли) равна

Эта разность потенциалов равна gh , где h разность уровней подъема воды в точках А относительно точки С, g – ускорение свободного па-

дения на поверхности Земли. Учитывая, что g = GMЗ находим пере-

RЗ2

пад подъемов воды при приливах, связанный с Луной,

3M R4

hЛ = 2r3 ЛMЗ ~ 0.55 м. (91.5)

ЛЗ З

Ответ для прилива за счет Солнца находится заменой MЛ MС ,

rЛЗ rСЗ :

3M R4

h С = 2r3 СMЗ ~ 0.24 м. (91.6)

СЗ З

Выше была рассмотрена статическая теория приливов, в которой горбы на воде появляются на линии Луна-Земля (средневзвешенным направлением между Луной-Солнцем и Землей). Более точная, динамическая теория учитывает движение приливной волны вокруг Земли. Не вдаваясь в детали можно сказать, что приливные силы можно считать вынуждающей силой, а период обхода волны вокруг Земли собствен-

Луна

Динамическая

Рис. 89

ной частотой осциллятора. Период обхода волны вокруг Земли оказывается больше периода вынуждающей силы. В этом случае, в соответ-

228

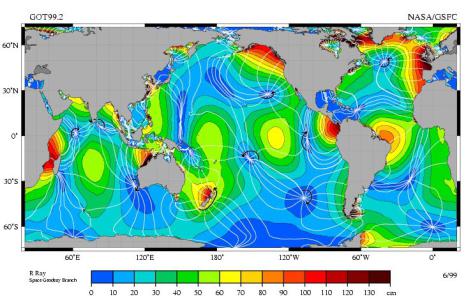
Рис. 90

ствие с теорией вынужденных колебаний осциллятора с малым затуханием (§ 57), амплитуда отстает от силы на p , т.е. на половину периода. Это приводит к тому, что горбы на воде будут находиться прямо противоположно тому, что предсказывает статическая теория (минимумы вместо максимумов и наоборот), рис 89.

Реально, наличие материков меняет эту картину до неузнаваемости. Так что физику явления нужно представлять, а реальную картину лучше не объяснять, а созерцать, отдыхая на берегах океанов и морей.

229

Г Л А В А XII

ГРАВИТАЦИЯ, ЭЛЕМЕНТЫ ОБЩЕЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ

§ 92. Введение

Ранее мы рассмотрели Специальную Теорию Относительности (СТО), которая описывает движение тел относительно инерциальных систем отсчета. При этом предполагалось, что пространство евклидово и сигналы связи, например, свет, распространяются по прямым линиям. При известном законе взаимодействия СТО, в принципе, позволяет рассчитать все движения тел при любых скоростях.

В таком подходе, однако, имеются проблемы при рассмотрении гравитационных взаимодействий. Силы гравитации действуют на все тела без исключения, в том числе и на свет. Траектории фотонов становятся "кривыми", и само пространство становится искривленным. Еще одна особенность – гравитационные поля создаются не только самими телами, но и любым видом энергии (в том числе гравитационной) и давлением. Принцип суперпозиции в достаточно сильных гравитационных полях не выполняется.

Явления, связанные с гравитацией, описывает Общая Теория Относительности (ОТО), созданная А. Эйнштейном (1916). Принцип относительности был распространен на системы, находящиеся в гравитационных полях. Ключом к решению задачи стал принцип эквивалентности. Гравитационные поля по своему действию очень похожи на силы, возникающие в неинерциальных (ускоренных) системах отсчета. В падающем лифте сила инерции и гравитационная сила компенсируются. Законы физики в такой системе будут совпадать с законами в инерциальных системах. Сидя в лифте нельзя сказать, какая часть силы вызвана гравитацией, а какая ускорением лифта. Разница заключается только в том, что силы инерции можно полностью исключить выбором системы отсчета, а истинно гравитационные силы можно скомпенсировать силами инерции только в точке. Так в падающем лифте пробное тело, помещенное в центре лифта, будет иметь нулевое ускорение относительно лифта, в верхней точке лифта сила тяжести немного меньше, поэтому тело будет ускоряться вверх, соответственно в нижней точке вниз.

230