telnov-mechanika-and-TO

Коэффициент Пуассона не может быть больше 0.5, иначе при прикладывании внешнего давления объем будет расти, и тело будет совершать работу. При снятии давления объем вернется к прежнему значению. Процесс можно повторить много раз, получается неисчерпаемый источник энергии, что невозможно.

Рассмотрим стержень, который не может расширяться вбок, т.к. с боков очень твердая среда. Тогда при приложении Pz возникают

Px ,Py , такие, что поперечные размеры не меняются

– модуль одностороннего сжатия. Например, если резинку поместить в металлическую трубку, то в продольном направлении у нее будет очень малая сжимаемость и, соответственно, очень большой эффективный модуль Юнга.

151

§ 61. Волны в среде, модель с шариками

Представим среду как линейку и стоящих вплотную шариков. Если крайнему шарику сообщить скорость, то он ударится о следующий шарик и остановится, передав ему весь свой импульс. Далее второй шарик ударит по третьему шарику, и остановится, и.т.д. В каждый момент в движении будет находиться только один шарик, а конце будет двигаться только последний шарик.

Если после того как первый шарик остановится, по нему снова ударить, то по цепочке побежит волна, состоящая из двух шариков. В конце, все шарики будут стоять, кроме двух последних.

Теперь заменим шарики тонкими пластинками, стоящими вплотную друг к другу (получается стержень), и начнем ударять по первой пластинке после каждой ее остановки. По стопке побежит волна длительностью равной времени воздействия на торец стержня. При устремлении толщины пластинки к нулю удары становятся бесконечно частыми, и воздействие сводится к действию постоянной силы.

Приравнивая (62.2) и (62.4), получаем скорость звука для среды, подчиняющейся закону Гука,

152

В общем случае, вместо (62.4) можно записать уравнение непрерывности на движущейся границе B. Переходим в систему отсчета движущегося фронта B, спереди фронта за единицу времени падает масса rc , а

за фронт уходит (c -v)(r +dr) . Из сохранения потока

В случае закона Гука, dr = -rldl = rdPE и для скорости звука по-

лучаем формулу (62.5). В курсе молекулярной физике, используя (62.7), будет получена скорость звука в газе

где g = сP . cV

Следует заметить, что формула (62.5) справедлива только для тонких стержней, когда ничего не мешает стержню расширяться вбок. В противном случае, вместо E нужно использовать E ¢ (ф-ла (60.8)), тогда продольная скорость

Эта скорость больше, чем в тонком стержне. Приближением толстого стержня работает в случаях: 1) стержень находится в очень жесткой трубке, 2) длина стержня короче толщины, 3) длина волны меньше толщины стержня.

153

Для справки: существуют еще и поперечные волны (частицы колеблются поперек движения волны). Для них

Поперечные волны существуют только в твердом веществе, в жидкости при сдвиге слоев не возникает возвращающих сил. Именно по этому признаку геологи различают твердые и жидкие породы.

§ 63. Волновое уравнение

Рассмотрим звуковую волну в газе. При распространении волны происходит 3 явления

1.Газ движется, плотность меняется.

2.При изменении плотности меняется давление.

3.Неравномерность давления вызывает движение газа.

Начнем с пункта 2. В общем случае P = f(r). В равновесии P0 = f (r0 ) . Отсюда отличие давления и плотности от равновесных значений в звуковой волне

Теперь используем явление 1. Пусть в волне продольное (X) смещение частиц y(x,t), и в данный момент времени это смещение различно для

точек с разными начальными координатами x . Тогда возникает изменение плотности. Пусть x невозмущенное положение частицы. В волне она сместится в точку x + y(x,t). Другая невозмущенная частица с ко-

ординатой x + Dx при этом сместится в точку x + Dx + y(x + Dx,t) . Частицы, которые находились в интервале Dx , теперь будут нахо-

154

второй член много меньше первого, т.к. смещения малы. Из сохране-

Наконец, явление 3 дает уравнение движения объема частиц в интервале Dx

Нетрудно убедиться, что решением волнового уравнения являются функции

т.е. любые функции, описывающие возмущения в среде, бегущие влево и вправо со скоростями c . Действительно, подставляя в (63.4) получа-

ем в левой части y¢¢c2 , в правой c2y¢¢ , где производная y¢¢берется по аргументу функции (t x / c) , т.е. решение (63.5) удовлетворяет вол-

новому уравнению (63.4). Это бегущая волна, поскольку, если в точке x = 0 в момент t = 0 было возмущение y(0), то такое же возмущение

будет через время t в точке x = ct . Таким образом, общее решение волнового уравнения

155

Принцип суперпозиции

Если в среде возбуждено несколько волн, и для каждой из них имеется решение вида (63.6), то нетрудно видеть, что и сумма этих волн является решением волнового уравнения линейного (в первой степени) по амплитуде. Это означает, что волны никак не влияют друг на друга, т.е. справедлив принцип суперпозиции.

Нетрудно сообразить, что для волн большой амплитуды это не так. Если изменение плотности в волне порядка самой плотности, то другие волны будут отражаться от таких перепадов плотности, так же как звуковая волна в воздухе отражается от стенок.

Ниже мы получим аналогичное уравнение для натянутой струны, а затем еще раз проанализируем решение волнового уравнения (63.5) и

поймем, как y1,2 зависят от начальных условий.

§ 64. Натянутая струна

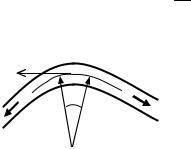
Рассмотрим струну, натянутую с силой T , по которой на некотором участке Dl частицы имеют малые смещения x в поперечном направлении. Соответствующее продольное

156

Уравнение движения по x

отсюда получаем волновое уравнение и скорость волны в натянутой струне

Получим скорость в струне другим, более элементарным способом. Пусть волна бежит по струне со скоростью c . Перейдем в систему бегущей волны. Струна имеет в точке горба возмущения некий радиус кривизны R , по которому перетекает масса струны. Частицы струны в этой системе отсчета испытывают центростремительное ускорение,

вызванное натяжением. Сила, действующая на участок малой длины l равна F = 2T sin a2 »Ta » TlR . Масса этого участка m = rSl , и ус-

корение

совпадающую с (64.3)

§ 65. Энергия в волне

157

Как нам известно, потенциальная энергия растянутой пружинки

В случае приложенной к торцу стержня силы в стержне бежит волна и, в соответствие с (62.3) и (62.5),

Таким образом, кинетическая и потенциальная энергии в бегущей волне равны!

§ 66. Начальные условия

Вернемся снова к общему решению волнового уравнения (63.6), состоящего из волн, бегущих в противоположные стороны. Предположим, в некоторой области произошло мгновенное увеличение давления (ударили по стержню сбоку), тогда в начальный момент есть только повышенное давление P в некоторой области, но частицы стержня никуда не движутся. Это состояние можно представить как две проти-

воположно бегущие волны, каждая с давлением P2 и скоростями час-

тиц в волне v . При наложении волн, в соответствие с принципом суперпозиции, давления и скорости сложились, давление стало P , а скорость ноль. В результате данное возмущение вызовет две одинаковые волны, бегущие в разные стороны. В данном примере в начальном состоянии была конечная потенциальная энергия и нулевая кинетическая. Если бы они были равны, то волна побежала бы в одну сторону, туда, куда направлена скорость частиц. В промежуточном случае (неравные потенциальные и кинетические энергии) возникнут две волны с неравными амплитудами.

158

§ 67. Столкновение стержня со стенкой, столкновение двух стержней

Столкновение со стенкой

Столкновение стержней разной длины.

Пусть короткий стержень налетает со скоростью v на покоящийся более длинный стержень. Перейдем в систему центра масс, движу-

щуюся со скоростью v2 . В этой системе стержни налетают с одинако-

вой скоростью и после столкновении их торцы остановятся и по стержням побегут волны сжатия. Торцы остановятся, поскольку пока

159

волны не сбегали туда-сюда в этом месте ничего не известно о длинах стержней. Т.е. вначале ситуация такая же как и при столкновении стержней одинаковой длины. Наконец по короткому стержню пробежала волна разряжения, и он долетел в обратном направлении. Во длинном стержне аналогичная волна разрежения еще не достигла границы столкновения, однако после отлета короткого стержня этот конец оказался свободным и от него пошла волна разряжения, а сам конец стал двигаться в вдогонку отлетающему короткому стержню с той же скоростью, но не давя на него. Далее в длинном стержне будут еще долго бегать волны сжатия и разряжения, но он уже не будет давить на короткий стержень. Перейдя обратно в лабораторную систему, мы находим, что короткий стержень остановился, а, стало быть, длинный стержень полетел с его импульсом (импульс всегда сохраняется).

Получился удивительный результат. Короткий стержень останавливается как в случае столкновения со стержнем той же длины, так и при столкновении с более длинным стержнем. В первом случае при соударении сохраняются и импульс и энергия (передаются покоящемуся стержню), а во втором случае энергия длинного стержня

P2 < P2 , следовательно, удар неупругий, хотя и сталкиваются аб-

2m2 2m1

солютно упругие тела. Тут нет никакого противоречия. Часть кинетическая энергия перешла в колебания длинного стержня, которые постепенно затухли, перейдя в хаотическое движение молекул, т.е. тепло.

Надо заметить, что продемонстрировать данный факт экспериментально очень трудно, поскольку нужен идеальный контакт торцов стержней.

§68. Стоячие волны

Пусть две синусоидальных волны бегут в противоположных направлениях:

где w - частота, k = 2lp . Фазовая скорость волны (точки с постоянной

фазой) c = wk . Это могут быть налетающая и отраженная от стенки волны. Суммарная амплитуда

160