
telnov-mechanika-and-TO
.pdfКак уже подчеркивалось, ко всем законам нужно относиться осторожно, они неточны при определенных условиях. Не исключено, что постоянная Планка и скорость света зависят от возраста Вселенной. Этот вопрос изучается, например, путем сравнения спектров атомов в лаборатории со спектром атомов от далеких звезд. Пока изменения фундаментальных констант во времени не обнаружено.
11
Г Л А В А II
НЕРЕЛЯТИВИВИСТСКАЯ КИНЕМАТИКА
§5. Пространство, время, системы координат
Вэтой главе мы будем рассматривать случай малых (нерелятивистских) скоростей, v c . Классическая механика опирается на следующие представления, почерпнутые из эксперимента:
1. В мире существуют тела, движущиеся под действием сил. Задание сил и начальных условий определяет полностью поведение системы в любой последующий момент времени.
2. Все физические процессы происходят в пространстве и времени. Предполагаются следующие свойства пространства:
• равноправие всех точек пространства (однородность);
• равноправие всех направлений (изотропность);
• евклидовость (сумма углов в треугольнике равна π).
Предполагается, что во всем пространстве можно ввести единое время, текущее везде равномерно и одинаково. По умолчанию предполагается, что движение тел никак не влияет на свойства пространства и времени.
Тела состоят из материальных точек, т.е. тел, размерами которых при рассмотрении можно пренебречь. В природе существуют твёрдые тела, в которых относительное расположение точек остаётся приблизительно неизменным. Их этих твердых тел можно сделать линейки для измерения расстояния между точками, выбрав одну из них за единицу масштаба. Между двумя точками можно провести бесконечное число линий. Кратчайшая из них называется прямой, а её длина расстоянием.
Точки пространства сами по себе не могут быть помечены, они имеют смысл только по отношению к материальным телам. Для описания пространства нужно указать тело отсчёта (или некоторое количество материальных точек, расстояние между которыми не изменяется). К этим телам можно прикрепить оси координат, а затем, используя жесткий масштаб (линейку), можно определить координаты любой точки. Координаты удаленных объектов можно найти также методом триангуляции, основанном на прямолинейном распространении света.
Совокупность тел, относительно которых определяется положение точек пространства, называется системой координат, а сами эти тела базисными. Минимальное количество тел, равное количеству чисел
12

необходимых для однозначного задания положения точек в пространстве, называется размерностью пространства. Мы живём в трехмерном пространстве. Задание, например, расстояний до трёх опорных точек задает координату в пространстве. Можно за три точки жестко закрепить декартову систему координат, тогда положение точки будет характеризоваться тремя числами (x,y,z ). Другие, наиболее популяр-
ные системы отсчета – это цилиндрическая и сферическая системы координат.
Для описания движения тел в пространстве нужно к системе опорных тел (системе координат) добавить еще часы в каждой точке пространства. Часами может быть любой периодический процесс, слабо зависящий от внешних воздействий. В классической механике предполагается, что все часы в пространстве независимо от движения идут одинаково, однако, это не так при больших скоростях. Система координат, снабженная часами, является системой отсчёта.
Декартова ( x,y ) и полярная (r,ϕ) системы координат на плоскости изображены на рис. 1 и 2.
Y |
|
Y |
x |
A |
A |
|
y |
r |
|
|
|
|
|
ϕ |
|
X |
X |
Рис. 1 |
|
Рис. 2 |
Переход от декартовых координат к полярным и обратно дается формулами
x = r cos ϕ |
r = x2 +y2 |
|
|
y = r sin ϕ |
ϕ = arctg |
y . |
(5.1) |
x |
|
||
|
|
|
|
13

Системы координат в пространстве: декартова (x,y,z ), цилиндрическая (r,ϕ,z ) и сферическая (r, θ,ϕ), показаны на рис. 3, 4 и 5. Декар-
Z Z
|
z |
z |
|
Y |
Y |
y |
x |
ϕ r |
X |
|
X |
Рис. 3 |
|
Рис. 4 |
това система в пространстве бывает двух видов: правая и левая. В правой системе (рис. 3-5) направление оси Z находится по правилу буравчика (штопора): при вращении ручки штопора в плоскости XY от оси X к оси Y он будет вкручиваться в направлении оси Z . Левой системе координат соответствует противоположное направление оси Z . Обычно используется правая система координат.
В сферической системе координат угол θ меняется от 0 до π , угол ϕ от 0 до 2π. Справа от рис.5 приведены формулы перехода сфериче-
ских к декартовым координатам и обратно.
|
Z |
|
x = r sin θcos θ |
||||||
|
|
|
y = r sin θsin θ |
||||||
|
r |
|
z = r cos θ |
|
|
(5.2) |
|||
θ |
|
|
|
|
|
|
|||
|
|
r = |
x2 +y2 |
|
+z2 |
||||
|
|
Y |
|
||||||
|
|
|
|
|
x |
2 |
+y2 |
|
|
ϕ |
|
|
θ = arctg |
|
|||||
|
|
|
|
|
z |
||||
X |
|
|
ϕ = arctg y |
|
|
||||
|
|
|
|
x |
|
|
|
|
|
Рис. 5
14
§ 6. Векторы
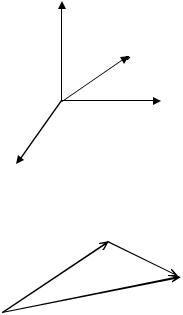
Положение можно также задать радиус-вектором r (или жирное r ) с началом в точке отсчета (O) и кон-
Zцом в рассматриваемой точке (A), рис. 6. Он имеет направление и длину r =| r |.
r |
A |
|
В каждой системе координат имеется |
||
|
|
однозначная связь между радиус- |
|||
|
|
|
|||
O |
|
Y |
вектором и координатами точки. При век- |
||
|
|
|
торном описании координат нужна лишь |
||
|
|
|
точка отсчета. |
|
|
|
|
|
Пример: пусть точка имела координа- |
||
X |
|
|
ту r1 |
относительно точки O . Затем точка |
|
Рис. 6 |
|
|
переместилась в точку r2 относительно |
||
|
|
|
исходного положения. Новый радиус век- |
||
r1 |
|
r2 |
тор |
относительно точки |
O будет |
|
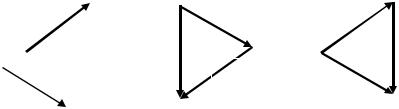
r3 = r1 + r2 . Графическое |
построение |
|||
(сложение векторов) показано на рис. 7 Векторный характер имеет не только
радиус-вектор, но и скорость, ускорение, сила, импульс и.т.д. Многие законы удобно записывать в векторном виде, получа-
ется более короткая запись, не нужно записывать уравнения по каждой проекции. Математически векторы могут быть представлены в виде строки с его компонентами в пространстве. Так радиус-вектор
r = (x,y,z) ≡ i x + jy + k z , |
(6.1) |
где i, j, k - единичные вектора в направлении осей X,Y,Z . То же для
вектора скорости |
|
v = (vx ,vy ,vz ) ≡ i vx + j vy + k vz . |
(6.2) |
Пример. Пусть скорость одного тела равна v1 , второго v2 , чему
равна их относительная скорость? |
|
По определению относительная скорость |
|
vотн = v2 − v1 = v2 +(−v1) . |
(6.3) |
15
Видим, что операция вычитания вектора эквивалентна прибавлению
v1 |
v2 |
v |
|
1 |
|
|
vотн |
vотн |
v2 |
−v1 |
v2 |
|
||
Рис. 8 |
Рис. 9 |
Рис. 10 |
вектора с противоположным направлением. Пристраивая вектор (−v1) к концу вектора v2 , рис. 9, находим построением вектор vотн .
Заметим, что относительную скорость можно найти более простым построением. Сведем начало векторов v1 и v2 в одну точку, рис.10.
Вектор, идущий от конца вектора v1 к концу вектора v2 , и будет вектор относительной скорости. Действительно, исходное выражение для относительной скорости vотн = v2 - v1 – то же самое, что и
v1 + vотн = v2 , соответствующее рис. 10. Для векторов создана векторная алгебра:
•b = γa - умножение на число
• |
c = a + b |
или |
cx |
= ax |
+bx , |
cy |
= ay |
+by – сложение |
• |
c = a − b |
или |
сx |
= ax |
-bx , |
сy |
= ay |
-by – вычитание |
• |
c = (ab) ≡ ab =| a || b | cosϕ – скалярное умножение |
|||||||
|
(c – скаляр, т.е. число, ϕ –угол между векторами). |
|||||||
• |
c = [ab] ≡ [a, b] ≡ a ×b – векторное умножение, |
|||||||
| c |=| a || b | sin ϕ. Направление вектора c перпендикулярно
aи b и находится по правилу буравчика при повороте a к
bпо кратчайшему пути, поэтому a × b = −b× a .
Для скалярного и векторного произведений работает распределительный закон: (a + b)c = ab + bc
Запишем скалярное и векторное произведение через компоненты векторов. Скалярное произведение двух векторов (ax ,ay,az ) и (bx ,by ,bz )
c = (ab) = (iax + jay + kaz )(ibx + jby + kbz ) = axbx +ayby +azbz (6.4)
16
при этом учтено, что (ii) = (jj) = (kk) = 1 , а (ij) = (jk) = (ik) = 0 .
Убедимся, что получается формула c = (ab) =| a || b | cosϕ .
Пусть a = (cos α, sin α), b = (cos β, sin β) , и ϕ = β −α, тогда
ab = cos αcos β + sin αsin β = cos(β −α) = cosϕ – все верно.
Найдем теперь компоненты векторного произведения:
c = a × b = (iax + jay + kaz )×(ibx + jby |
+ kbz ). |
(6.5) |
Учитывая что |
|
|
i × j = -j× i = k, j× k = -k × j = i, k × i = -i × k = j |
|
|
(используется правая система координат), получаем |
|
|
c = i(aybz −azby ) + j(azbx −axbz ) + k(axby |
−aybx ) . |
(6.6) |
Впринципе можно придумать и другие операции векторами, но они не применяются, т.к. для них не работает распределительный закон.
Вданном курсе нам понадобятся еще произведения трех векторов:
a(b× c) = (a × b)c = (c× a)b , |
(6.7) |
в результате такого произведения получается скаляр, соответствующий объему параллелепипеда, построенного из этих векторов.
Еще одно произведение трех векторов – это двойное векторное произведение
a ×(b× c) = b(ac) - c(ab) . |
(6.8) |
Здесь в результате получается вектор. Это выражение можно получить прямой проверкой.
§ 7. Прямая задача кинематики, скорость и ускорение
Прямая задача кинематики заключается в нахождении скорости v(t) из известного r(t)и ускорения a(t) из v(t) и. Рассмотрим сначала
одномерную задачу.
Мгновенная скорость v = |
x |
при t → 0 в момент времени |
|
t |
|
t = t0 , будет ни что иное, как производная функции x(t), равная тан-
генсу угла наклона между касательной к графику и положительным направлением оси t .
17

X
x(t)
|
|
|
|
|
|
|
|
|
t0 |
|
t |
|
|
||
|
|
|
|
|
|
|
Рис. 11 |
|
|
|
|
|
|||
|
Производная функции x(t) в точке t0 |
|
|
|
(7.1) |
||||||||||
|
|
|
|
dx(t0) = x(t0 +dt) −x(t0) . |
|
||||||||||
|
|
|
|
|
|
|
|
t→0 |
|
|
|
|
|
||
|
|
|
|
|
dt |
|
|
|
|
dt |
|
|
|
|
|
|
Рассмотрим |
простейший пример: x(t) = at2 , |
где a = const . |
||||||||||||
Подставляя в (7.1) получаем |
|
|
|
dt→0 |
|
||||||||||
|
|
|
|
|
|
|
|
|
2at dt +a(dt) |
|
|
|
|||
dx(t0) = a(t +dt) |
−at |
2 |
= |
|
|
|
2 |
= 2at +adt = 2at . (7.2) |
|||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
dt |
|
|
|
|
|
|
|
dt |
|
|
|
|
|
Используются различные обозначения производной:
dx(t) - по Лейбницу dt
x′(t)- по Лагранжу
x - по Ньютону
Все это мгновенная скорость v(t). Ускорение, по определению
a(t) = v(t +dt) −v(t) = dv |
≡ v′(t) ≡ v(t) |
(7.3) |
|||
|
dt |
|
dt |
|
|
Выразивv(t) через x(t) , получаем |
|
|
|
||
a(t) = |
d2x(t) |
≡ x |
′′ |
|
(7.4) |
dt2 |
(t) = x(t). |
||||
Выпишем производные от элементарных функций, часто встречающихся в физических задачах (подробности в курсе мат. анализа)
18
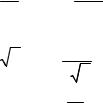
f (x)
const
xn
1
xn x
x
1 x
f ′(x)
0
nxn−1
−xnn+1
1
1
2x
−x12
f(x) |
f ′(x) |
|
ex |
ex |
|
ln x |
1 / x |
|
sin x |
cos x |
(7.5) |
cos x |
−sin x |
|
tg x |
1 / cos2 x |
|
ctg x |
−1 / sin2 x |
|
Дифференцирование произведения и дроби функций: Пусть f (x) = u(x)v(x) , тогда
df |
= |
|
u(x +dx)v(x +dx) −u(x)v(x) |
= |
|
|
|
dx |
|
|
|||||
|
|
|
dx |
|
|
|
|
|
(u(x) +u′(x)dx)(v(x) +v′(x)dx) −u(x)v(x) |
(7.6) |
|||||
|
= |
|
|
|
|
= |
|
|
|
|
dx |
|
|||
|
|
|
|
|
|
|
|
|
dx→0 |
|
|
|
|
||
|
|
|
′ |
′ |
|
|
|
|
= u (x)v(x) +u(x)v (x) |
|
|
|
|||
Аналогично находятся производные от любых произведений и дробей, в частности
f (x) |
|
|
f |
′ |
|
|
|
|
|
|
|
(x) |
|
|
|
|
|||
u(x)v(x) |
|
′ |
|
′ |
|
|
|
|
|
u (x)v(x) +u(x)v (x) |
|
|
|
|
|||||
u(x)v(x)g(x) |
|
′ |
|
|
′ |
′ |
(7.7) |
||
u (x)v(x)g(x) +u(x)v |
|
(x)g(x) +u(x)v(x)g (x) |
|
||||||
u(x) |
|
u |
′ |
′ |
|
|
|
|
|
|
(x)v(x) −u(x)v (x) |
|
|
||||||
v(x) |
|
|
|
|
v2(x) |
|
|
|
|
19

Дифференцирование сложной функции:
Пусть есть
Например: dudf = 2u,
f (u), где u = g(x). Тогда
|
df = df du . |
|
(7.8) |
|
|
dx |
du dx |
|
|
f (x) = sin2 x . Здесь |
f = u2 , где |
u = sin x . Находим |
||
du |
= cos x , следовательно df |
= 2 sin x cos x = sin 2x . |
||
dx |
|
dx |
|
|
Используя эти довольно простые правила, можно найти производную от любой функции, являющейся комбинацией элементарных математических функций. Задача всегда имеет решение.
При движении в пространстве удобно использовать векторное описание, при этом мгновенная скорость, рис. 12,
r |
v(t) = lim r(t + t) − r(t) |
= dr |
(7.9) |
|||||||||
|
t→0 |
|
|
t |
|
|
|
|
|
dt |
|
|
r(t + dt) |
Аналогично |
|
a(t) = dv |
= d2r . |
(7.10) |
|||||||
r(t) |
|
|
|
|
dt |
|
|
dt2 |
|
|||
|
В декартовых кординатах |
|
|
|
|
|||||||
|
|
|
|
|
|
|
dy |
|
dz |
|
|
|
|
v = (v |
,v |
,v |
|
dx |
, |
, |
|
(7.11) |
|||
Рис. 12 |
|
) = |
|
|
|
. |
||||||
x |
y |
|
z |
|
|
dt |
|
dt |
|
|
||
|
|
|
|
|
dt |
|
|
|
|
|||
vz |
Годограф |
Конец вектора r(t) описывает |
|||
траекторию в X,Y,Z -пространстве. По |
|||||
|
скорости |
аналогии можно нарисовать то же для |
|||
|
v(t) |
скорости, рис. 13. Такую кривую в |
|||
|
|
||||
|
vy |
пространстве |
скоростей |
называют |
|
vx |
годограф скорости. Он показывает |
||||
|
|||||
|
какие значения принимает скорость во |
||||
время движения.
Рис. 13
20
