
ТФКП и ОП
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Государственное образовательное учреждение высшего профессионального образования МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ "МАМИ"
Коган Е.А.
УЧЕБНОЕ ПОСОБИЕ
по курсу ‘Теория функций комплексной переменной и операционное исчисление” для студентов всех специальностей и направления подготовки дипломированных специалистов и бакалавров
очного и очно – заочного отделений
Одобрено методической комиссией по математическим и естественно-научным дисциплинам
Москва
2011
2
Разработано в соответствии с Государственным образовательным стандартом ВПО 2000 г. для всех специальностей и направления подготовки дипломированных специалистов и бакалавров очного и очно – заочного отделений на основе рабочей программы дисциплины “Математика’.
Рецензенты: проф., д. т. н. Балакирев Ю.Г., кафедра «ПиВМ», вед. науч. сотр., к. ф.- м. н, Король Е.З. НИИ
механики МГУ.
Работа подготовлена на кафедре «Прикладная и вычислительная математика» им. Э.И.Григолюка
Теория функций комплексной переменной и операционное исчисление. Учебное пособие по дисциплине " Математика" для студентов всех специальностей и направления подготовки дипломированных специалистов и бакалавров очного и очно – заочного отделений. МГТУ «МАМИ». 2011. - 190 стр.
Пособие предназначено для изучения раздела дисциплины “Математика”, посвященного теории функций комплексной переменной и операционному исчислению. Оно содержит теоретические сведения в объëме лекционного курса и подробно разобранные примеры решения типовых задач. Приведены также варианты тестовых заданий и РГР. Пособие может быть использовано студентами в качестве руководства для самостоятельной работы и преподавателями для проведения практических занятий. -
Библ. 10. Рис. - 56.
© Коган Е.А. © МГТУ «МАМИ», 2011

3
ВВЕДЕНИЕ
На протяжении многих столетий в математике происходило последовательное обобщение понятия числа. От натуральных (целых положительных) чисел в математике перешли к целым (положительным и отрицательным) числам, затем к рациональным (дробным), далее к действительным (включающим и иррациональные) числам. Каждое расширение понятия числа открывало возможности решения новых задач, казавшихся до этого неразрешимыми. Так произошло и с комплексными числами.
Как известно, алгебраическое уравнение второй степени ax2 +bx +c = 0 имеет действительные корни, если дискриминант
уравнения D = b2 − 4ac ≥ 0. Первым, кто рассмотрел задачи, не удовлетворяющие этому условию, был Джеронимо Кардано1 (1545 г.). Он обнаружил, что если дискриминант квадратного уравнения D < 0, то вычисление корней сводится к извлечению квадратного корня из отрицательного числа (что невозможно в области действительных чисел). Полученные числа он назвал “софистическими”.
Позднее Р.Декарт2 в приложении к своему труду “Рассуждение о методе, чтобы хорошо направить свой разум и отыскивать истину в науках” (1637 г.), рассматривая алгебраическое уравнение n – ой степени, показал, что оно имеет всегда n корней, но среди них возможны, кроме действительных, и “воображаемые” (названные им мнимыми) корни.
Формальное математическое определение мнимого числа было дано Л.Эйлером3 в работе “Введение в математический анализ” (1746 г.). Используя первую букву предложенного Р.Декартом термина (мнимый – imaginares). Л.Эйлер определил
1Кардано Джеронимо (24.09.1501 – 21.09.1576) – итальянский математик.
2Декарт Рене (31.03.1596 – 11.02.1650) – французский математик и философ.
3Э й л е р Леонард (15.04.1707 – 18.09.1783) – швейцарский математик, механик и физик (с 1727 г. по 1741г. и с 1766 г. до конца жизни жил и работал в России).

4
мнимую единицу равенством i2 = −1 (так как действительных чисел, которые при возведении в квадрат были бы отрицательными, не существует).
Введение мнимого числа было отнюдь не тривиальным шагом и потребовало исторически длительного периода осмысления нового понятия. Это подтверждается, например, так называемым “парадоксом Карно4”. Парадокс состоял в следующем преобразовании:
|
i2 = −1 |
−1 = |
(−1)(−1) = 1 = ±1. |
|
||
Таким образом, получалось, что i2 |
равно и −1 и |
+1. При- |
||||
веденное |
преобразование |
связано |
с |
применением |
равенства |
|
a b = |
ab. Справедливость |
его |
доказывается в |
алгебре в |
||
предположении, что числа |
a, b и ab положительны, как и значе- |
|||||
ния корней из этих чисел. В рассматриваемом же случае числа
−1 и |
−1 не являются положительными. Поэтому равенство |
a b = |
ab, доказанное в алгебре при указанных выше огра- |
ничениях, было применено для других условий, что и привело к неверному выводу.
Последовательную геометрическую интерпретацию и современное обозначение новых чисел, назвав их комплексными, дал К.Гаусс5 в работе “Теория биквадратных вычетов” (1799 г.) и позднее в работе “Арифметическая теория комплексных чисел”
(1806, 1825 и 1831 гг.).
Введение комплексных чисел и основанных на них функций комплексной переменной оказалось весьма удобным при интегрировании элементарных функций, при решении дифференциальных уравнений, где часто приходится выходить за пределы области действительных чисел. Основанные на понятии комплексного числа методы теории функций комплексной переменой оказались весьма эффективными и позволили решить многие новые задачи в таких сложных областях естествознания и техники, как аэро – и гидродинамика, теория горения и взрыва, плоская
4Карно Никола Леонард Сади (01.06.1796 – 24.08.1832) – французский физик и инженер.
5Гаусс Карл Фридрих (30.04.1777 – 23.02.1855) – немецкий математик.
5
задача теории упругости, механика разрушения, технологические задачи теории пластичности и др.
Основные понятия теории функций комплексной переменной и операционного исчисления изложены в пособии в сжатой, но доступной, по мнению автора, для понимания форме, максимально приближенной к лекционным и практическим занятиям. Для лучшего усвоения теоретического материала и выполнения расчетно – графической работы по курсу в пособии приведено достаточно большое количество примеров. Варианты расчетно – графической работы (РГР) по теории функций комплексной переменной и операционному исчислению составлены проф. Е.А.Лопаницыным. Включены также вопросы по теории и несколько вариантов тестов для самоконтроля. Решение их полезно студентам для лучшей подготовки к экзамену, а преподавателями аналогичные по структуре тесты могут быть использованы для проверки текущей успеваемости студентов.

6
1.КОМПЛЕКСНЫЕ ЧИСЛА
ИДЕЙСТВИЯ НАД НИМИ
Комплексным числом z называется выражение вида
z = x +iy, |
(1.1) |
где x и y – действительные числа, а |
i - символ, называемый |
мнимой единицей, удовлетворяющий условию i2 = −1.
Числа x и y называются соответственно действительной и
мнимой частями комплексного числа и обозначаются символами: x = Re(x +iy) = Re z, y = Im(x +iy) = Im z 6.
Таким образом, комплексное число характеризуется комплексом (парой) действительных чисел с установленным порядком следования этих чисел.
Запись комплексного числа в форме (1.1) называется алгеб-
раической формой записи.
В частности, при y = 0 комплексное числоz = x +i 0 = x совпадает с действительным числом, при x = 0 z = 0 +iy = iy и
называется чисто мнимым числом.
Определим на множестве комплексных чисел понятия равенства и алгебраические операции.
Два комплексных числа z1 = x1 +iy1 и z2 = x2 +iy2 равны тогда и только тогда, когда равны соответственно их действи-
тельные и мнимые части: x1 = x2 и |
y1 = y2 . |
|||||
Комплексное число x −iy называется сопряженным с чис- |
||||||
лом z = x +iy и записывается в виде z = x −iy. |
||||||
Очевидно, Re z = |
z + z |
, Im z = |
z − z |
= i |
z − z |
. |
|
2i |
|
||||
2 |
|
2 |
|
|||
Сложение и умножение комплексных чисел производятся по правилам сложения и умножения алгебраических многочленов.
Суммой комплексных чисел z1 = x1 +iy1 и z2 = x2 +iy2 на-
зывается комплексное число
z = z1 + z2 = x1 + x2 +i( y1 + y2 ).
Сложение допускает обратную операцию - вычитание: комплекс-
6 Re – начальные буквы латинского слова realis – действительный, Im - начальные буквы слова imaginarius – мнимый.
|
|
7 |
|
ное |
число z = z1 − z2 = x1 − x2 +i( y1 − y2 ) называется |
разностью |
|
комплексных чисел z1 и |
z2 . |
|
|
|
Произведением комплексных чисел z1 и z2 называется ком- |
||
плексное число вида |
|
|
|
|
z = z1z2 = x1x2 − y1 y2 +i(x1 y2 + x2 y1 ). |
z1 = z2 = i, |
|
Из этого определения, в частности, следует, что если |
|||
то |
i2 = −1. |
|
|
|
Заметим, что так как возведение в целую положительную |
||
степень сводится к последовательному умножению, то |
|||
|
i3 = i2i = −i, |
i4 = i3i = −ii =1, i5 = i4i = i,... |
|
Как видно, значение степени мнимого числа in периодически повторяется при увеличении показателя степени на 4. Поэтому при возведении мнимого числа в некоторую степень, большую четырех, можно в показателе степени отбросить число,
кратное четырем. Например, |
|
i145 = i144+1 = i1 = i. |
|
|
||||||||||||||||
Умножение также допускает обратную операцию - деление |
||||||||||||||||||||
(если делитель не равен нулю). |
|
|
|
|
|
|
|
|||||||||||||
Частным двух чисел ( z2 |
≠ 0) называется комплексное число |
|||||||||||||||||||
|
|
|
|
z = |
z1 |
|
= |
x1x2 + y1 y2 |
+i |
y1x2 − y2 x1 |
. |
(1.2) |
||||||||
|
|
|
z2 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
x22 + y22 |
|
|
x22 + y22 |
|
|
||||||
Действительно, выражение (1.2) получается, если дробь ум- |
||||||||||||||||||||
ножить на комплексное число z2 , сопряженное знаменателю |
||||||||||||||||||||
z = |
z1 |
= |
x1 +iy1 |
= |
x1 +iy1 |
|
x2 −iy2 |
= |
x1x2 + y1 y2 |
+i |
y1x2 − y2 x1 |
. |
||||||||
|
z2 |
x2 +iy2 |
x2 +iy2 |
|
x2 −iy2 |
|
|
x22 + y22 |
x22 + y22 |
|||||||||||
Из приведенных определений следует, что для комплексных чисел, как и для действительных, справедливы переместительный, сочетательный законы сложения и умножения и распределительный закон:
z1 + z2 = z2 + z1, |
z1 +(z2 + z3 ) = (z1 + z2 ) + z3 , |
z1z2 = z2 z1, |
z1 (z2 z3 ) = (z1z2 )z3 , |
(z1 + z2 )z3 = z1z3 + z2 z3.
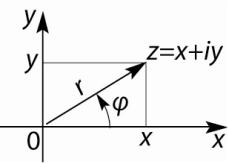
1.1. Геометрическая интерпретация комплексного числа
Как известно, существует взаимно однозначное соответствие между множеством действительных чисел и множеством то-
8
чек числовой оси (прямой): каждому действительному числу соответствует одна определенная точка на числовой оси и наоборот. Так как комплексное число представляется парой действительных чисел, то оказалось возможным дать и комплексному числу наглядную геометрическую интерпретацию, изображая его точкой плоскости с координатами (x, y).
Введем систему декартовых прямоугольных координат на плоскости x0 y . Число z = 0 ставится в соответствие началу ко-
ординат. При этом действительные числа x будут изображаться точками оси абсцисс x, которую будем называть действительной осью, а чисто мнимые числа – точками оси ординат, которую будем называть мнимой осью. Определенную таким образом плоскость будем называть плоскостью комплексной переменной или комплексной плоскостью (рис. 1). И обратно, каждой точке плоскости x0 y с координатами (x, y) может быть поставлено в
соответствие комплексное число z = x +iy. Таким образом, между
множеством всех комплексных чисел и всех точек плоскости установлено взаимно однозначное соответствие.
Рис. 1
Заметим, что сопряженные комплексные числа на комплексной плоскости будут изображаться точками, симметричными относительно действительной оси
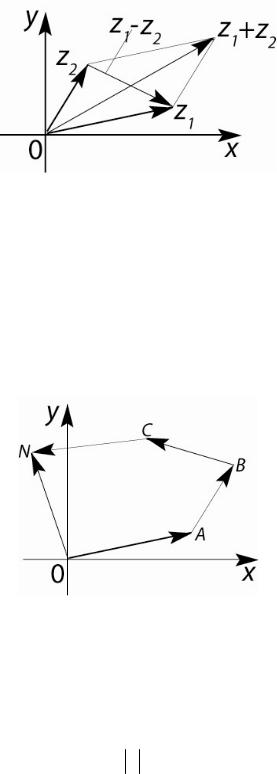
Действительной и мнимой частям комплексного числа можно также поставить в соответствие координаты радиуса – вектора точки, изображающей комплексное число, то есть проекции его на оси координат. Следовательно, комплексные числа можно изображать и с помощью векторов на плоскости. Поэтому операции сложения и вычитания комплексных чисел имеют наглядный
9
геометрический смысл: сумма и разность комплексных чисел z1 и z2 изображаются соответствующими векторами, равными (по
правилу суммы и вычитания векторов) диагоналям параллелограмма, построенного на векторах z1 и z2 (см. рис. 2).
Рис. 2
Сумма нескольких комплексных чисел изобразится геометрической суммой векторов, изображающих эти числа. Для этого из конца первого вектора проводят вектор, равный второму, из конца второго вектора откладывают вектор, равный третьему и т.д. В результате, суммой n векторов будет вектор ON, соединяющий начало первого вектора с концом последнего n -го вектора (см. рис. 3).
Рис. 3
Положение точки, изображающей комплексное число z , можно также характеризовать полярными координатами r и ϕ
(рис. 1).
Полярный радиус r называется модулем комплексного числа и обозначается символом r = z . Это длина вектора, соответ-
ствующего комплексному числу z :
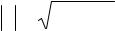
10
r = z = x2 + y2 ≥ 0.
Следовательно, модуль комплексного числа – это неотрицательное действительное число (равное нулю только, если z = 0),
определенное однозначно.
Угол ϕ, образованный радиусом-вектором r с положитель-
ным направлением оси x, называется аргументом комплексного числа и обозначается символом ϕ = Arg z. Правило знаков для
угла ϕ принято таким же, как в тригонометрии, а именно, он счи-
тается положительным, если отсчитывается от положительного направления действительной оси против часовой стрелки (рис. 1).
Очевидно, при повороте на угол, кратный 2π , конец радиу- са-вектора будет попадать в одну и то же точку на плоскости, соответствующую одному и тому же комплексному числу z . Поэтому аргумент комплексного числа – величина многозначная, определяемая лишь с точностью до слагаемого, кратного 2π . В качестве главного значения аргумента обычно принимают его наименьшее значение, заключенное обычно в промежутке
−π < arg z ≤π , либо 0 ≤ arg z < 2π.
Будем в дальнейшем считать, что главное значение аргумента удовлетворяет условию −π < arg z ≤π .
Заметим, что при принятом условии главное значение аргумента претерпевает разрыв на отрицательной полуоси: при приближении точки z к точке отрицательной полуоси сверху arg z → +π, а при приближении к той же точке отрицательной
полуоси снизу arg z → −π.
Вся совокупность значений аргумента определяется равенством
Arg z = arg z + 2kπ,
где k = 0,±1,±2,... - произвольное целое число.
При z = 0 и при z = ∞ Arg z не определен. Из чисто геомет-
рических соображений ясно, что если z = x > 0 - положительное действительное число, то arg z = 0; если z совпадает с действи-
тельным отрицательным числом (z = x < 0) , то arg z =π; если z - чисто мнимое число с положительной мнимой частью, то
