
ТФКП и ОП
.pdf
41
рактеризуется тем, что бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Для функции комплексной переменной это означает, что если точка z окажется внутри круга радиуса δ с центром в точке z0 , то соответствующая точка w попадет внутрь круга радиуса ε
с центром в точке w0 = f (z0 ), построенного в плоскости w (рис. 17).
Рис. 17
Функция f (z) называется непрерывной в области, если она непрерывна в каждой точке этой области.
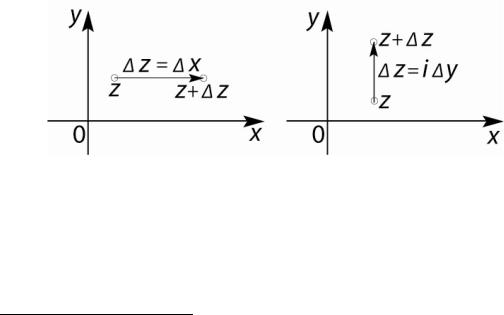
Дадим |
независимой переменной z = x +iy приращение |
∆z = ∆x +i∆y |
и найдем соответствующее приращение функции |
w = f (z) : ∆w = f (z + ∆z) − f (z).
Производной функции f (z) в точке z называется предел
отношения приращения функции к приращению аргумента при стремлении ∆z к нулю по любому закону:
f ′(z) = lim ∆w .
∆z→0 ∆z
Замечание. Так как на комплексной плоскости геометрическое место точек, равноудаленных от точки z на расстояние ∆z , представляет собой окружность радиуса ∆z (см. рис. 17), то требование существования производной для функции комплексной переменной, как следует из определения, означает существование предела ∆w / ∆z при стремлении точки z + ∆z к точке z по любому пути (в частности по любому из бесчисленного множества радиусов) и равенство всех этих пределов. Это требование является значительно более жестким по сравнением с аналогичным требованием для функций действительной переменной и приво-
42
дит к тому, что дифференцируемые функции комплексной переменной обладают рядом дополнительных свойств по сравнению с функциями действительной переменной.
2.5. Условия Коши – Римана9
Пусть f (z) = u(x, y) +iv(x, y) и приращение аргумента ∆z = ∆x +i∆y. Тогда приращение функции будет равно
∆w = f (z + ∆z) − f (z) = ∆u +i∆v,
где ∆u = u(x + ∆x, y + ∆y) −u(x, y), ∆v = v(x + ∆x, y + ∆y) −v(x, y).
Поэтому |
′ |
∆w |
= lim |
∆u +i∆v |
. |
f (z) = lim |
∆z |
∆x +i∆y |
|||
|
∆z→0 |
∆x→0 |
|
||
|
|
|
∆y→0 |
|
|
Пусть этот предел существует и по определению не зависит от закона стремления ∆z = ∆x +i∆y к нулю. Рассмотрим два слу-
чая.
Пусть, например, точка z + ∆z стремится к точке z по прямой, параллельной оси 0x (см. рис. 18). Тогда ∆z = ∆x и поэтому
′ |
∆w |
= lim |
∆u +i∆v |
= lim |
|
∆u |
+ |
i∆v |
= |
∂u |
+i |
∂v |
. |
(2.17) |
f (z) = lim |
∆z |
∆x |
|
∆x |
|
∂x |
∂x |
|||||||
∆z→0 |
∆x→0 |
∆x→0 |
|
∆x |
|
|
|
|
||||||
|
Рис. 18 |
Найдем тот же предел в предположении, что точка z + ∆z |
|
приближается к точке z |
по прямой, параллельной мнимой оси |
(рис.18). Тогда, очевидно, |
∆z = i∆y. Поэтому |
9 Коши Огюстен Луи (21.08.1789 – 23.08.1857) – французский математик и механик.
Риман Георг Фридрих Бернхард (17.09.1826 – 20.07.1866) – немецкий математик.

|
|
|
|
43 |
|
|
|
|
|
|
|
|
|
|
|
′ |
∆w |
|
∆u +i∆v |
|
|
∆u |
|
i∆v |
|
∂v |
|
∂u |
|
|
|
f (z) = lim |
∆z |
= lim |
i∆y |
= lim |
|
|
+ |
|
|
= |
∂y |
−i |
∂y |
. |
(2.18) |
|
|
||||||||||||||
∆z→0 |
∆y→0 |
∆y→0 i∆y |
|
i∆y |
|
|
|
|
|||||||
Так как выражения (2.17) и (2.18) должны совпадать, то
приходим к равенству |
∂u |
+i |
∂v |
= |
∂v −i |
∂u , |
откуда следуют со- |
|
отношения |
∂x |
|
∂x |
|
∂y |
|
∂y |
|
∂u = |
∂v |
|
|
∂u |
= − ∂v . |
|
||
|
, |
|
(2.19) |
|||||
|
∂x |
∂y |
|
|
∂y |
|
∂x |
|
Эти условия называются условиями Коши – Римана (Да-
ламбера – Эйлера10) и являются необходимыми и достаточными условиями дифференцируемости функции комплексной переменной.
Нами доказана необходимость выполнения этих условий для того, чтобы функция была дифференцируемой. Если, кроме того, частные производные функций u(x, y) и v(x, y) будут не-
прерывными в области, то условия Коши – Римана будут и достаточными условиями аналитичности функции.
Функция комплексной переменной f (z) , дифференцируе-
мая в каждой точке некоторой области, называется аналитиче-
ской (или регулярной) в этой области.
Те точки области, в которых функция является аналитической, называются правильными, а те точки области, в которых функция перестает быть аналитической (или не определена), называются особыми.
Замечание. Так как основные теоремы о пределах и определение предела для функции комплексной переменной не отличаются от соответствующих теорем и определений для функций действительной переменной, то формально техника дифференцирования функций комплексной переменной является такой же, как и для функций действительной переменной. Другими словами, правила дифференцирования и теоремы дифференцирования
10 Эти условия значительно раньше О.Коши и Г.Римана были получены Ж.Л.Даламбером (1752) и Л.Эйлером (1755, 1777). Даламбер Жан Лерон (16.11.1717 – 29.10.1783) – французский математик и философ.

44
сложных функций действительной переменной остаются справедливыми и для функций комплексной переменной.
Пример. |
Проверить аналитичность функций: а) |
w = z + 1 |
; |
||||||||||||||||||||||||
б) w = cosiz ; |
|
в) |
w = e2z + 2 cos3z . Найти их производные. |
z |
|
||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
а) Полагая z = x +iy |
|
находим действительную и мнимую |
|||||||||||||||||||||||||
части функции |
w: |
|
|
|
|
|
x |
−iy |
|
|
|
|
|
|
x |
|
|
|
y |
|
|
||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
w = x +iy + |
|
|
|
|
|
= x +iy + |
|
|
|
|
|
= x + |
|
|
|
|
+i y − |
|
, |
|
|||||||
|
x |
+iy |
|
x2 + y2 |
x2 |
+ y2 |
x2 + y2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
u(x, y) = x + |
|
x |
|
|
|
, v(x, y) = y − |
|
|
|
y |
|
|
- функции, дифферен- |
||||||||||||||
x2 + y2 |
|
|
x2 + y2 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
цируемые всюду, кроме точки x = 0, y = 0. |
|
|
|
|
|
|
|
||||||||||||||||||||
Проверяем выполнение условий Коши – Римана: |
|
|
|
|
|||||||||||||||||||||||
∂u |
=1− |
|
x2 − y2 |
|
|
, |
∂v |
=1− |
|
x2 − y2 |
, |
|
|
|
|||||||||||||
|
∂x |
(x2 + y2 )2 |
∂y |
(x2 + y2 )2 |
|
|
|
||||||||||||||||||||
∂u |
= − |
|
|
|
2xy |
|
, |
|
∂v |
= |
|
|
2xy |
|
. |
|
|
|
|
||||||||
|
∂y |
|
(x2 + y2 )2 |
|
|
∂x |
(x2 + y2 )2 |
|
|
|
|
||||||||||||||||
Как видно, условия Коши - Римана выполняются всюду, кроме точки z = 0. Следовательно, функция w = z + 1z аналитична
всюду на комплексной плоскости с “выколотым центром”. Еë производная равна w′ =1-1/z2 .
б) |
w = cosiz = cosi(x −iy) = cos( y +ix) = |
|
|
||
= cos y cos ix −sin y sin ix = cos ychx −i sin yshx. |
|
||||
Функции u(x, y) = cos ychx и |
v(x, y) = −sin yshx |
дифферен- |
|||
цируемы при любых значениях x |
и y. Их частные производные |
||||
имеют вид: ∂u |
= cos yshx, |
∂v = −cos yshx. Так как |
∂u |
≠ ∂v , то |
|
∂x |
|
∂y |
|
∂x |
∂y |
условия Коши – Римана нигде в плоскости z не выполняются, следовательно, функция w = cosiz не является аналитической ни в одной точке плоскости.
в) e2z = e2( x+iy) = e2 xe2iy = e2 x (cos 2 y +isin 2 y) =

45
= e2 x cos 2 y +ie2 x sin 2 y,
cos3z = cos(3x +3iy) = cos3x cos3iy −sin 3x sin 3iy = = cos 3x ch 3y −i sin 3x sh 3y,
w = e2 x cos 2 y + 2 cos 3x ch 3y +i(e2 x sin 2 y −2sin 3x sh 3y). u(x, y) = e2 x cos 2 y + 2 cos 3x ch 3y, v(x, y) = e2 x sin 2 y − 2sin 3x sh 3y.
Поэтому
∂∂ux = 2e2 x cos 2 y −6sin 3x ch 3y = ∂∂yv ,
∂∂uy = −2e2 x sin 2 y +6 cos3x sh 3y = − ∂∂vx .
Так как условия Коши – Римана выполняются, то функция w аналитическая всюду на плоскости, следовательно,
w′ = dwdz = 2e2z −6sin 3z.
2.6. Связь аналитических функций с гармоническими
Как известно, гармонической в области функцией называется действительная функция u(x, y) двух действительных пере-
менных, обладающая в этой области непрерывными вторыми частными производными и удовлетворяющая дифференциальному уравнению в частных производных второго порядка
∆u = ∂2u + ∂2u = 0. ∂x2 ∂y2
Это уравнение называется уравнением Лапласа11. Оно (и соответственно гармонические функции) играет важную роль в математической физике.
Можно показать, что если функция комплексной переменной f (z) = u(x, y) +iv(x, y) однозначна и аналитична в некоторой
области, то в этой области еë действительная и мнимая части являются гармоническими функциями.
11Лаплас Пьер Симон (23.03.1749 – 05.03.1827) – французский математик, астроном и физик.
46
Вместе с тем, не из любых двух дифференцируемых функций u(x, y) и v(x, y) можно составить дифференцируемую функ-
цию комплексной переменной, так как для функции u(x, y) +iv(x, y) условия Коши – Римана могут не выполняться.
Аналитическую функцию f (z) = u(x, y) +iv(x, y) можно по-
строить, если произвольно задав одну из двух гармонических функций (u(x, y) или v(x, y) ), подобрать другую так, чтобы
удовлетворялись условия Коши – Римана. Для этого надо определить вторую из функций по еë полному дифференциалу.
Рассмотрим эту процедуру на примере: найти аналитическую функцию w = f (z), если u(x, y) = x3 −3xy2 , f (0) = i.
Находим сначала |
|
∂u |
= 3x2 −3y2 . Так как должно выпол- |
||||
|
∂u |
|
∂v |
|
∂x |
∂v |
|
няться условие |
= |
, |
то |
= 3x2 −3y2 , откуда следует |
|||
|
∂x |
|
∂y |
|
|
∂y |
|
v = ∫(3x2 −3y2 )dy +ϕ(x) = 3x2 y − y3 +ϕ(x),
где ϕ(x) - произвольная функция интегрирования. Дифференци-
цируя последнее равенство по x, |
находим |
|
|
|||
∂v |
′ |
∂v |
∂u |
∂u |
′ |
|
∂x = 6xy + |
ϕ (x), |
а так как ∂x = − ∂y , то |
∂y = −6xy |
−ϕ (x). |
||
Но из условия следует, что ∂u |
= −6xy. Приравнивая производные, |
|||||
|
′ |
∂y |
|
′ |
Поэтому ϕ(x) = C. |
|
|
|
|||||
находим −6xy −ϕ (x) = −6xy. |
ϕ (x) = 0. |
|||||
Итак, |
|
v(x, y) = 3x2 y − y3 +C , |
|
|
||
|
|
|
||||
f (z) = u(x, y) +iv(x, y) = x3 −3xy2 +i (3x2 y − y3 +C). |
||||||
Теперь из условия |
f (0) = i , |
то есть при |
x = y = 0 , |
находим: |
||
f (0) = i = Ci, |
C =1. Окончательно получаем |
|
||||
f (z) = x3 −3xy2 +i (3x2 y − y3 +1).
Выразим далее f (z) как функцию аргумента z. Так как z = x +iy,
z = x −iy, то x = |
z + z |
, |
y = |
z − z |
. |
|
2i |
||||
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
47 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
+ z 3 |
|
z + z |
z |
− z |
2 |
z + z 2 z − z |
|
|
|||||||||||||
w = f (z) = |
|
|
|
|
− |
3 |
|
|
|
|
|
|
+i 3 |
|
|
|
|
|
− |
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
2 |
|
2 |
|
2i |
|
|
2 2i |
|
|
|
|||||||||||
z − z 3 |
|
|
|
z3 |
+3z2 z +3zz 2 |
+ z3 |
|
3(z3 − z2 z − zz 2 + z3 ) |
|
||||||||||||||||
− |
|
|
+1 |
= |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
+ |
|||
|
|
|
|
8 |
|
|
|
|
|
8 |
|
|
|
||||||||||||
|
2i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
+ 3(z2 z + z3 − zz 2 − z3 ) + |
z3 −3z2 z +3zz 2 − z3 |
+i = z3 +i. |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
8 |
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
2.7. Геометрический смысл аргумента и модуля производной от аналитической функции
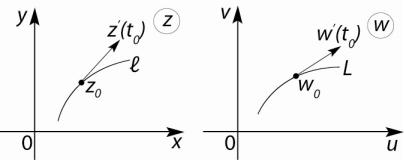
1. Пусть f (z) - аналитическая функция в некоторой области комплексной плоскости z. Возьмëм какую – нибудь точку z0
в этой области и проведем через неë произвольную кривую l
(см. рис. 19).
|
|
Рис. 19 |
|
|
Пусть |
при |
отображении, |
осуществляемом функцией |
|
w = f (z), точка z0 |
переходит в точку w0 , |
а образом кривой l бу- |
||
дет кривая L , проходящая через точку w0 |
на плоскости w. |
|||
Так как функция f (z) аналитична по условию, то она имеет |
||||
производную |
′ |
|
что в точке z0 эта производ- |
|
f (z). Предположим, |
||||
ная не равна нулю: |
f ′(z0 ) ≠ 0. Зададим уравнение кривой l в па- |
|||
раметрической форме: z = z(t), где t - некоторый параметр. Тогда уравнение кривой L при отображении, осуществляемом функци-
ей |
w = f (z), будет |
иметь вид: |
w = f [z(t)] и в точке w0 |
w0 |
= f [z(t0 )] = w(t0 ). |
По правилу |
дифференцирования сложной |
функции w′(t0 ) = f ′(z0 ) z′(t0 ). |
|
||

48
Учитывая, что при умножении комплексных чисел их аргументы складываются, получим Arg w′(t0 ) = Arg f ′(t0 ) + Arg z′(t0 ).
Очевидно, величина f ′(z0 ) , а значит и Arg f ′(z0 ) , не зависит от выбора кривой l , а зависит только от вида функции f (z) и точки z0 . Поэтому можно принять Arg f ′(z0 ) =α = const.
В результате приходим к выводу о том, что аргумент производной от аналитической функции имеет наглядный геометрический смысл: он равен углу, на который надо повернуть касательную в точке z0 к любой кривой, проходящей через эту точку,
чтобы получить направление касательной в соответствующей точке w0 к образу данной кривой при отображении, осуществ-
ляемом функцией w = f (z). При этом, если arg f ′(z0 ) > 0, то по-
ворот происходит против часовой стрелки и наоборот. Следовательно, если через точку z0 провести какую - ни-
будь другую кривую так, чтобы угол между касательными к кривым был равен ϕ, то при отображении, осуществляемом анали-
тической функцией, угол между касательными к образам этих кривых в плоскости w будет также равен ϕ.
2. Рассмотрим далее геометрический смысл модуля производной. Так как ∆z - это расстояние от точки z0 до точки z0 + ∆z , а
∆w - расстояние от точки w0 до точки w0 + ∆w, то величина ∆w / ∆z показывает, в каком отношении меняется расстояние
между соответствующими точками при отображении, осуществляемом функцией w = f (z). Предел этого отношения и есть мо-
дуль производной:
|
|
f ′(z0 ) |
|
|
|
|
∆w |
|
∆w |
|
= k. |
(2.20) |
|||
|
|
|
= |
lim |
= lim |
|
|||||||||
|
|
|
|||||||||||||
|
|
|
|
f ′(z0 ) |
|
|
∆z→0 |
∆z |
∆z→0 |
∆z |
|
|
|
||
Величину |
k = |
|
|
называют коэффициентом растяже- |
|||||||||||
|
|
||||||||||||||
ния в точке z0 |
при отображении |
w = f (z). Если k >1, |
то в дос- |
||||||||||||
таточно малой окрестности точки z0 расстояния между точками
увеличиваются (происходит растяжение) и наоборот.
Из соотношения (2.20) с точностью до величин высшего порядка малости следует приближенное равенство: ∆w ≈ k ∆z . Гео-

49
метрически это означает, что при отображении, осуществляемом аналитической функцией, бесконечно малые линейные элементы преобразуются подобным образом. Это свойство называют свой-
ством постоянства растяжения.
Отображение окрестности точки z0 на окрестность точки w0 , осуществляемое аналитической функцией w = f (z) и обла-
дающее свойствами постоянства растяжений и сохранения (консерватизма) углов между линиями (во всех точках, где производ-
ная f ′(z0 ) ≠ 0), называется конформным отображением.
Понятие конформного отображения является одним из важнейших в математике. Конформные отображения аналитических функций находят широкое применение для решения различных сложных задач механики (в гидро – и аэродинамике, плоской и неоднородной теории упругости), физики (в теории электростатического, магнитного и теплового полей), в картографии. Оказывается, что во многих случаях при решении задач для областей сложной формы (например, профиль крыла самолета, отверстие некруговой формы и т.п.) можно конформно отобразить заданную область сложного очертания на область простой формы (например, на единичный круг), для которой соответствующая задача или уже решена, или решение находится просто. Обратный переход производится с помощью той же функции, которая осуществляет конформное отображение. Существенный вклад в развитие и применение этих методов к задачам механики сплошной
среды внесен отечественными учеными Н.Е.Жуковским12, С.А.Чаплыгиным13, Г.В.Колосовым14, Н.И.Мусхелишвили15.
12Жуковский Николай Егорович (17.01.1847 - 17.03.1921) - механик, основоположник авиационной науки.
13Чаплыгин Сергей Алексеевич (05.04.1869 - 08.09.1942) - математик и механик, академик АН СССР.
14Колосов Гурий Васильевич (24.081867 - 07.09.1936) - механик, чл.-корр. АН СССР.
15Мусхелишвили Николай Иванович (16.02.1891 -15.07.1976) - математик и механик, академик АН СССР.
50
3. ИНТЕГРАЛЫ ОТ ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
3.1 Понятие контурного интеграла от функции комплексной переменной
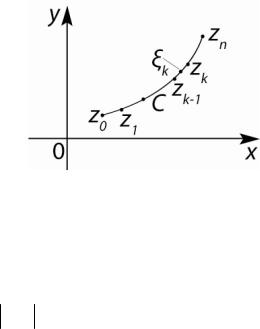
Рассмотрим на плоскости комплексной переменной гладкую (или кусочно – гладкую) кривую C, начальную и конечную точки которой обозначим соответственно через z0 и zn . Тем самым на-
ми установлено положительное направление обхода кривой. Пусть функция f (z) = u(x, y) +iv(x, y) непрерывна во всех точках
этой кривой.
Разобъем кривую C на n частей (рис. 20) точками z1, z2 ,...zn−1 так, что zk = xk +iyk , и составим так называемую интегральную
n
сумму ∑ f (ξk )∆zk , где ξk - произвольно взятая точка на элемен-
k=1
тарной дуге zk−1zk , f (ξk ) - значение функции в точке ζk ,
∆zk = zk − zk−1.
Рис. 20
Определенным (контурным) интегралом от функции комплексной переменной, взятым вдоль кривой C, называется предел построенной интегральной суммы, когда число частичных дуг стремится к бесконечности, а длина наибольшей из них стремится к нулю: (max ∆zk → 0 )
|
zn |
|
|
|
|
|
n |
∫ f (z)dz = ∫ f (z)dz = n→∞lim |
∑ f (ξk )∆zk . |
||||||
C |
z0 |
max |
|
∆zk |
|
→0 k=1 |
|
|
|
||||||
Так как z = x +iy, |
dz = dx +idy, то |
|
|||||
