ТФКП и ОП
.pdf151
ПРИЛОЖЕНИЕ 3
ВАРИАНТЫ РАСЧЕТНО – ГРАФИЧЕСКОЙ РАБОТЫ
ПО ТЕОРИИ ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ И ОПЕРАЦИОННОМУ ИСЧИСЛЕНИЮ
152
Вариант №1
1.Записать комплексное число a = 1 + 
3 i в тригонометрической и показательной формах и показать его положение на комплексной плоскости x0y с указанием модуля и аргумента.
2.Выполнить указанные действия с двумя комплексными чис-
лами a = 1 + 
3 i и b = 2 + 3i: a + b, a – b, a b, a/b, a4, 3 a .
3.Вычислить функцию w = 3ez +sin z при z = 2 + 3i и показать числа z и w на комплексных плоскостях x0y и u0υ.
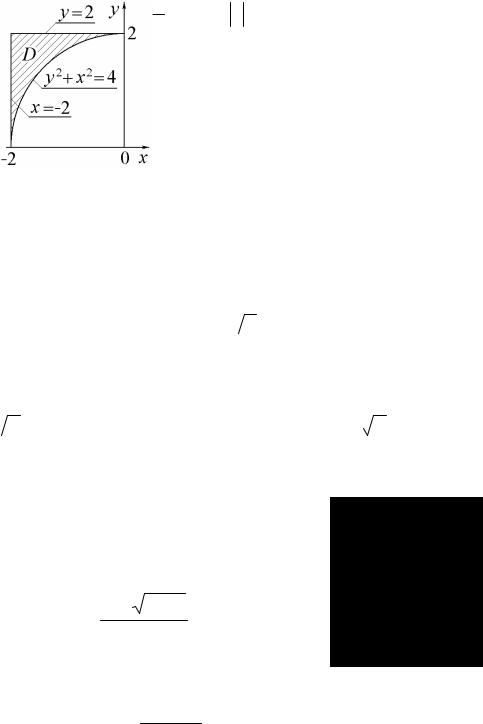
4.Построить отображение области D на плоскости x0y на плоскость u0υ с помощью функции комплексной переменной w = 1/z.
5.Вычислить предел
lim |
1 −cos z . |
z→0 |
z2 |
6. Найти все нули и особые точки функции комплексной переменной и указать их тип
w = sin z .
z2
7.Проверить функцию комплексной переменной w = zez на аналитичность и найти её производную.
8.Вычислить определённый интеграл функции комплексной переменной (z2 +1)
1+i
∫tgzdz .
0
9.Вычислить интеграл функции комплексной переменной по замкнутому контуру С, применяя интегральную формулу Коши и теорему Коши о вычетах
∫ |
z3 + 2z2 +1 |
dz, C : z +1 = 2 . |
(z + 2)2 |
||
С |
|
|
10. Найти изображение F(p) по Лапласу функции действительной переменной f(t) = e–2tch3t sin2t.
11. Найти оригинал f(t) по его изображению по Лапласу
F (p)= |
p2 + 4 p + 5 |
. |
|
||
|
p3 + 2 p2 + 5p |
|
153
12.С помощью преобразования Лапласа решить задачу Коши для
линейного дифференциального уравнения с постоянными ко- y′′+ 9 y )= 2, y′(0)= 0 (t ≥ 0).эффициентами = −18sh3t, y(0
Вариант № 2
1.Записать комплексное число a = 1 – 
3 i в тригонометрической и показательной формах и показать его положение на комплексной плоскости x0y с указанием модуля и аргумента.
2.Выполнить указанные действия с двумя комплексными чис-
лами a = 1 – 
3 i и b = 1 +3i: a + b, a – b, a b, a/b, a3, 4 a .
3. Вычислить функцию w = 2ez − cos 2z при z = 1 + 3i и показать числа z и w на комплексных плоскостях x0y и u0υ.
4.Построить отображение области D на плоскости x0y на плоскость u0υ с помощью функции комплексной
переменной w = 1/z.
5.Вычислить предел
lim1 − 3 1 − z .
z→0 z
6.Найти все нули и особые точки функции комплексной переменной и указать их тип
w = sinz z .
7.Проверить функцию комплексной переменной w = 2z + 3sin z на аналитичность и найти её производную.
8.Вычислить определённый интеграл функции комплексной переменной
1∫−isin(zlnz)dz .
1
9.Вычислить интеграл функции комплексной переменной по замкнутому контуру С, применяя интегральную формулу Коши и теорему Коши о вычетах
∫ z2dz =
С (z2 +1)(z −1), C : z 2 .
154
10.Найти изображение F(p) по Лапласу функции действительной переменной f(t) = 2sin2t + 5e–2t.
11.Найти оригинал f(t) по его изображению по Лапласу
F (p)= |
p +1 |
p2 (p2 −5p + 6). |
12.С помощью преобразования Лапласа решить задачу Коши для линейного дифференциального уравнения с постоянными ко-
эффициентами |
y |
′′ |
+ 4 y |
′ |
+ 2 y = e |
2t |
′ |
(t ≥ 0). |
|
||||||||
|
|
|
, y(0)=1, y (0)=1 |
Вариант № 3
1.Записать комплексное число a = –1 + 
3 i в тригонометрической и показательной формах и показать его положение на комплексной плоскости x0y с указанием модуля и аргумента.
2.Выполнить указанные действия с двумя комплексными чис-
лами a = –1 + 
3 i и b = 2 + i: a + b, a – b, a b, a/b, a4, 3 a .
3.Вычислить функцию w = ez − 3chz при z = 2 + i и показать числа z и w на комплексных плоскостях x0y и u0υ.
4.Построить отображение области D на плоскости x0y на плоскость u0υ с помощью функции комплексной переменной w = 1/z.
5.Вычислить предел
lim |
3 − |
5 + z . |
z→4 |
1 − |
5 − z |
6.Найти все нули и особые точки функции комплексной переменной и указать их тип
w= (z z+2i)3 .
7.Проверить функцию комплексной переменной w = z2 + 2ez на аналитичность и найти её производную.
8.Вычислить определённый интеграл функции комплексной переменной
i |
z2dz |
|
∫0 |
|
. |
z3 − 2 |
||
155
9.Вычислить интеграл функции комплексной переменной по замкну тому контуру С, применяя интегральную формулу Коши и теорему Коши о вычетах
∫ dz , C : 2 z =1.
С z(z +1)(z + 2)
10. Найти изображение F(p) по Лапласу функции действительной переменной f(t) = tetcos2t.
11. Найти оригинал f(t) по его изображению по Лапласу
F (p)= |
p + 4 |
|
|
. |
|
p3 − 3p2 + 2 p |
||
12.С помощью преобразования Лапласа решить задачу Коши для
линейного дифференциального уравнения с постоянными ко- 4 y )= 0, y′(0)=1 (t ≥ 0).y′′+эффициентами = t, y(0
Вариант № 4
1.Записать комплексное число a = –1 – 
3 i в тригонометрической и показательной формах и показать его положение на комплексной плоскости x0y с указанием модуля и аргумента.
2.Выполнить указанные действия с двумя комплексными чис-
лами a = –1 – 
3 i и b = 3 + i: a + b, a – b, a b, a/b, a4, 3 a .
3.Вычислить функцию w = ez + 2sh2z при z = 3 + i и показать числа z и w на комплексных плоскостях x0y и u0υ.
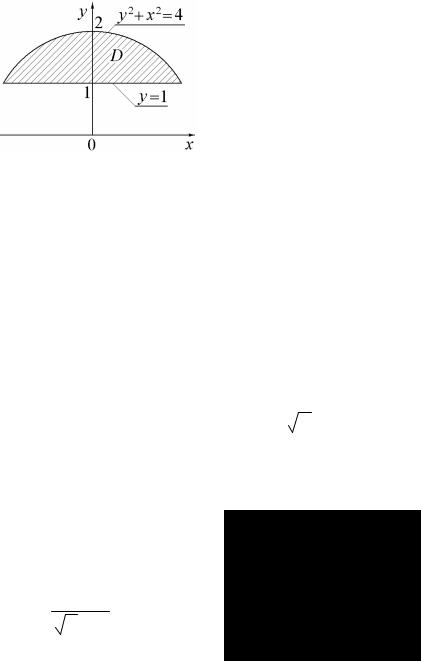
4.Построить отображение области D на плоскости x0y на плоскость u0υ с помощью функции комплексной переменной w = 1/z.
5.Вычислить предел
lim |
2 − z −3 . |
z→7 |
z2 − 49 |
6.Найти все нули и особые точки функции комплексной переменной и указать их тип
w = (ez++1)2 . z 1
7.Проверить функцию комплексной переменной w = 4cos(2z +1) на аналитичность и найти её производную.
156
8. Вычислить определённый интеграл функции комплексной переменной
1+i
∫sin4 z cos zdz .
−i
9.Вычислить интеграл функции комплексной переменной по замкнутому контуру С, применяя интегральную формулу Коши и теорему Коши о вычетах
∫С z2 (zdz+ 2)2 , C : 2 z = 3.
10.Найти изображение F(p) по Лапласу функции действительной переменной f(t) = te–tsint.
11.Найти оригинал f(t) по его изображению по Лапласу
F (p)= |
p + 4 |
|
|
. |
|
p(p2 + 4) |
||
12.С помощью преобразования Лапласа решить задачу Коши для
линейного дифференциального уравнения с постоянными ко- y′′− 2 y′−8y )= 2, y′(0)=1 (t ≥ 0).эффициентами = sint, y(0
Вариант № 5
1.Записать комплексное число a = 3 + 3i в тригонометрической и показательной формах и показать его положение на комплексной плоскости x0y с указанием модуля и аргумента.
2.Выполнить указанные действия с двумя комплексными чис-
лами a = 3 + 3i и b = 1 +2i: a + b, a – b, a b, a/b, a4, 3 a .
3. Вычислить функцию w = 3sin z + cos2z при z = 1 + 2i и показать числа z и w на комплексных плоскостях x0y и u0υ.
4.Построить отображение области D на плоскости x0y на плоскость u0υ с помощью функции комплекс-
ной переменной w = 1/z.
5.Вычислить предел
lim |
|
z −8 . |
z→8 |
3 |
z − 2 |
6.Найти все нули и особые точки функции комплексной переменной и указать их тип
157
tgz
w)3 .
7.Проверить функцию комплексной переменной w = 3z sin z на аналитичность и найти её производную.
8.Вычислить определённый интеграл функции комплексной переменной = (z + i
2+i
∫4z sin z cos zdz .
0
9.Вычислить интеграл функции комплексной переменной по замкнутому контуру С, применяя интегральную формулу Коши и теорему Коши о вычетах
dz |
|
∫С (z −1)(z + 2)2 |
, C : z = 3. |
10. Найти изображение F(p) по Лапласу функции действительной переменной f(t) = e2tcos2t.
11. Найти оригинал f(t) по его изображению по Лапласу
F (p)= (p −1)p(p2 +1).
12.С помощью преобразования Лапласа решить задачу Коши для
линейного дифференциального уравнения с постоянными ко- y′′− 2 y′ = cost, y )= 0, y′(0)=1 (t ≥ 0).эффициентами (0
Вариант № 6
1.Записать комплексное число a = 3 – 3i в тригонометрической и показательной формах и показать его положение на комплексной плоскости x0y с указанием модуля и аргумента.
2.Выполнить указанные действия с двумя комплексными чис-
лами a = 3 – 3i и b = 1 + i: a + b, a – b, a b, a/b, a4, 3 a .
3.Вычислить функцию w = 4shz − ch3z при z = 1 + i и показать числа z и w на комплексных плоскостях x0y и u0υ.
4.Построить отображение области D на плоскости x0y на плоскость u0υ с помощью функции комплексной пе-
ременной w = 1/z.
5.Вычислить предел
|
|
158 |
lim |
|
z −1. |
z→1 |
3 |
z −1 |
6. Найти все нули и особые точки функции комплексной переменной и указать их тип
w = |
z3 + 2z2 +1 |
. |
|
(z + 2)2 |
|
||
7.Проверить функцию комплексной переменной w = 2z cos z на аналитичность и найти её производную.
8.Вычислить определённый интеграл функции комплексной пе-
ременной
1+i
∫sin3 z cos2 z dz .
0
9.Вычислить интеграл функции комплексной переменной по замкнутому контуру С, применяя интегральную формулу Коши и теорему Коши о вычетах
∫ zdz , C : z = 2 .
С (z −i)(z − 3)
10. Найти изображение F(p) по Лапласу функции действительной переменной f(t) = tch2t.
11. Найти оригинал f(t) по его изображению по Лапласу
F (p)= |
1 |
. |
p(p2 − 9) |
12.С помощью преобразования Лапласа решить задачу Коши для линейного дифференциального уравнения с постоянными коэффициентами
y |
′′′ |
− 4 y |
′′ |
= −2e |
|
′ |
′′ |
(t ≥ 0). |
|
|
3t |
, y(0)= 0, y (0)= 2, y |
(0)=1 |
||||
|
|
|
|
|
|
|
|
Вариант № 7
1.Записать комплексное число a = –3 + 3i в тригонометрической и показательной формах и показать его положение на комплексной плоскости x0y с указанием модуля и аргумента.
2.Выполнить указанные действия с двумя комплексными числа-
ми a = –3 + 3i и b = 2 + 2i: a + b, a – b, a b, a/b, a4, 3 a .
3. Вычислить функцию w = 2sin z + chz при z = 2 + 2i и показать числа z и w на комплексных плоскостях x0y и u0υ.
159
4.Построить отображение области D на плоскости x0y на плоскость u0υ с помощью функции комплексной
переменной w = 1/z.
5.Вычислить предел
lim |
1 + z − 1 − z . |
z→0 |
z |
6.Найти все нули и особые точки функции комплексной переменной и указать их тип
w = ( 2 + z)2( − ). z 1 z 1
7. Проверить функцию комплексной переменной w = z + 2cos z на аналитичность и найти её производную.
8.Вычислить определённый интеграл функции комплексной переменной
1+i |
dz |
||
∫0 |
|||
|
. |
||
z2 + 4z +5 |
|||
9. Вычислить интеграл функции комплексной переменной по замкнутому контуру С, применяя интегральную формулу Коши и теорему Коши о вычетах
∫( z−+1)2 dz, C : z = 4.
С z 3
10. Найти изображение F(p) по Лапласу функции действительной переменной f(t) = tsh3t.
11. Найти оригинал f(t) по его изображению по Лапласу
F (p)= ( − )(p2++1)( − ).
p 1 p 2 p 3
12.С помощью преобразования Лапласа решить задачу Коши для линейного дифференциального уравнения с постоянными ко- эффициентами (0)=1, y′(0)=1, y′′(0)= 0 (t ≥ 0).
Вариант № 8
1.Записать комплексное число a = –3 – 3i в тригонометрической и показательной формах и показать его положение на комплексной плоскости x0y с указанием модуля и аргумента.
160
2. Выполнить указанные действия с двумя комплексными числа-
ми a = –3 – 3i и b = 3 + 2i: a + b, a – b, a b, a/b, a4, 3 a .
3. Вычислить функцию w = cos 2z + 3shz при z = 3 + 2i и показать числа z и w на комплексных плоскостях x0y и u0υ.
4.Построить отображение области D на плоскости x0y на плоскость u0υ с помощью функции комплекс-
ной переменной w = 1/z.
5.Вычислить предел
lim |
z + 4 − 2 . |
z→0 |
z |
6. Найти все нули и особые точки функции комплексной переменной и указать их тип
= sin z
w z(z +1)(z + 2).
7. Проверить функцию комплексной переменной w = 3sin z2 на аналитичность и найти её производную.
8. Вычислить определённый интеграл функции комплексной переменной
2i
∫tg3z dz .
0
9.Вычислить интеграл функции комплексной переменной по замкнутому контуру С, применяя интегральную формулу Коши и теорему Коши о вычетах
∫С (z −ezπ )3 dz, C : z = 5
10.Найти изображение F(p) по Лапласу функции действительной переменной f(t) = 2sh2t cos3t.
11.Найти оригинал f(t) по его изображению по Лапласу
F (p)= |
3p2 − 2 p +1 |
. |
|
||
|
p3 + 5p2 + 4 p |
|
12.С помощью преобразования Лапласа решить задачу Коши для линейного дифференциального уравнения с постоянными ко- эффициентами (0)= 0, y′(0)= 3, y′′(0)=1 (t ≥ 0).