
ТФКП и ОП
.pdf
|
|
91 |
|
|
|
|
|
f2 |
(z) = |
z2 − 4 |
|
= |
z − 2 |
. |
|
z(z +3)(z + 2)4 |
z(z +3)(z + 2)3 |
||||||
|
|
|
|
||||
Полагая теперь z(z +3)(z + 2)3 = 0, |
находим, что z = 0 и z = −3 - |
||||||
простые нули, а z = −2 - нуль третьего порядка. Поэтому для заданной функции точки z = 0 и z = −3 являются простыми полюсами, а точка z = −2 - полюсом третьего порядка.
Замечание. Как видно из этих примеров, если известно, что точка z = z0 является полюсом функции, то для определения его
порядка можно и не разлагать функцию в ряд Лорана.
4.4. Понятие вычета функции. Основная теорема о вычетах
Пусть z = z0 - изолированная особая точка аналитической функции. Тогда в окрестности этой точки функция f (z) может быть разложена в ряд Лорана
n=∞ |
|
1 |
f (z)dzn+1 . |
f (z) = ∑Cn (z − z0 )n , где |
Cn = |
||
n=−∞ |
|
2πi C∫(z − z0 ) |
|
Коэффициент C−1 при минус первой степени (z − z0 ) в раз-
ложении функции в ряд Лорана в окрестности конечной изолированной особой точки z0 называется вычетом функции f (z) от-
носительно особой точки z0 и обозначается символом
Res[ f (z); z0 ] = C−1 = 21πi C∫ f (z)dz .
Здесь C – произвольный замкнутый контур, охватывающий точку z0 и проходимый в положительном направлении (напри-
мер, окружность малого радиуса).
Пусть функция f (z) аналитична внутри простого замкнуто-
го контура C и на нем, за исключением конечного числа изолированных особых точек: z0 , z1,..., zn . Проведем окружности мало-
го радиуса с центрами в этих точках так, чтобы они лежали целиком внутри контура C , не пересекались между собой и чтобы внутри каждой из них находилось лишь по одной особой точке
( рис. 32).
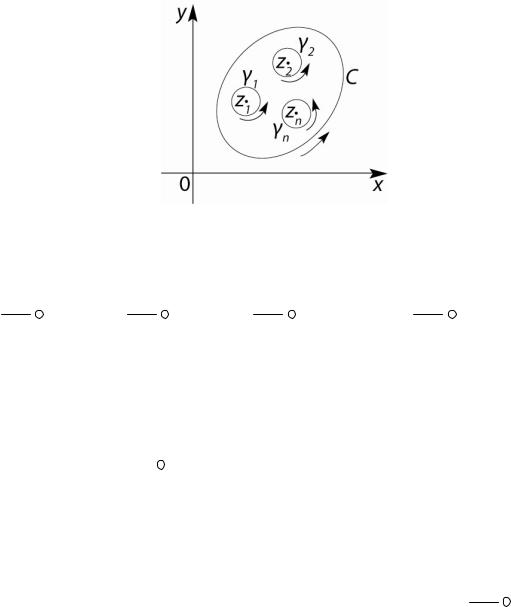
92
Рис. 32
Тогда по теореме Коши для сложного контура можно запи-
сать
1 |
∫ f (z)dz = |
1 |
∫ f (z)dz + |
1 |
∫ f (z)dz +... + |
1 |
∫ f (z)dz. |
2πi |
C |
2πi |
γ1 |
2πi |
γ2 |
2πi |
γn |
|
|
|
|
Но каждое из слагаемых в правой части представляет собой вычет функции относительно соответствующей особой точки zi (i =1,2,..., n). Поэтому
|
n |
|
∫ f (z)dz = 2πi∑Res[ f (z); zk ]. |
(4.32) |
|
C |
k=1 |
|
Итак, нами доказана следующая основная теорема о вычетах: если функция f (z) аналитична всюду в области, ограничен-
ной простым замкнутым контуром, за исключением конечного
числа изолированных особых точек, то величина |
1 |
∫ f (z)dz |
|
2πi |
C |
равна сумме вычетов подынтегральной функции |
f (z) |
относи- |
тельно всех еë особых точек, лежащих внутри области. Важность основной теоремы о вычетах заключается в том,
что она позволяет свести вычисление контурных интегралов от аналитических функций комплексной переменной к вычислению вычетов подынтегральной функции относительно еë особых точек, расположенных внутри контура, то есть к вычислению дифференциальных величин, какими являются вычеты.
4.5. Техника вычисления вычетов
Если точка z = z0 является устранимой особой точкой, то в разложении этой функции в ряд Лорана, как известно, отсутству-

93
ет главная часть. Поэтому вычет функции относительно устранимой особой точки равен нулю.
Если в точке z = z0 функция имеет существенно особую
точку, то вычет функции относительно этой точки находится с помощью разложения функции в ряд Лорана и непосредственного определения коэффициента C−1.
Если точка z = z0 - простой полюс функции f (z) , то при
разложении функции в ряд Лорана в окрестности этой точки в главной части будет только один член, поэтому еë можно представить в виде
f (z) =ϕ(z) + |
C−1 |
, |
(4.33) |
|
|||
|
z − z0 |
|
|
где ϕ(z) - сумма правильной части разложения функции в ряд Лорана: ϕ(z) является аналитической, а потому, тем более непрерывной функцией в точке z0 . Из формулы (4.33) находим
|
C−1 = (z − z0 ) f (z) −(z − z0 )ϕ(z). |
|
||
Перейдем к пределу при z → z0 . Так как функция ϕ(z) не- |
||||
прерывна в точке z0 , то существует конечный предел |
|
|||
limϕ(z) =ϕ(z0 ) , поэтому lim[(z − z0 )ϕ(z)] = 0. |
|
|||
z→z0 |
z→z0 |
|
||
Отсюда следует, что вычет функции относительно простого |
||||
полюса равен |
Res[ f (z); z0 ] = lim[(z − z0 ) f (z)]. |
(4.34) |
||
|
||||
|
z→z0 |
|
||
Если функция f (z) , аналитическая в окрестности простого |
||||
полюса z = z0 |
, представляет собой дробь f (z) = |
f1 (z) |
, |
причем |
|
||||
|
|
f2 (z) |
|
|
f2 (z0 ) = 0, а |
f1 (z0 ) ≠ 0, то удобнее применить иную формулу для |
|||
вычета функции, выполнив преобразование формулы (4.34):
Re s[ f (z); z0 ] = lim[(z − z0 ) |
f1 |
(z) |
] = |
|
f2 |
(z) |
|||
z→z0 |
|
|||
|
|
|
lim f1 (z)
z→z0 =
lim f2 (z)
z→z0 z − z0
94
= |
|
|
|
f1 (z0 ) |
|
|
|
|
|
|
= |
f1 (z0 ) |
. |
||
|
f |
2 |
(z) − f |
2 |
(z |
0 |
) |
|
|
′ |
|||||
|
lim |
|
|
|
|
|
|
|
f |
2 (z0 ) |
|
||||
|
|
z − z0 |
|
|
|
|
|
|
|
||||||
|
z→z0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, |
|
|
|
|
|
|
|
|
|
f1 (z0 ) |
|
|
|||
|
Res[ f (z); z0 ] = |
|
|
|
. |
(4.35) |
|||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
f2′(z0 ) |
|
|||
Если точка z = z0 является полюсом n – го порядка для функции f (z) , то можно показать, обобщая равенство (4.34), что справедлива формула
Res[ f (z); z0 ] = |
1 |
lim |
d n−1 |
[(z − z0 )n f (z)]. |
(4.36) |
|
dzn−1 |
||||
|
(n −1)! z→z0 |
|
|
||
Примеры. Найти вычеты функций относительно полюсов:
1) |
f (z) = |
z |
+1 |
|
; |
2) |
f (z) = |
|
1 |
|
|
; |
3) |
f (z) = |
ez −1 |
|
; |
|||||||||
(z −1)(z − 2)2 |
z4 |
+ |
1 |
z(z +1) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
4) |
f (z) = z3 sin |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1) Функция f (z) |
|
имеет простой полюс z0 =1 и полюс вто- |
|||||||||||||||||||||||
рого порядка z0 |
= 2. По формуле (4.34) находим |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
z +1 |
|
|
|
|
|
|
z +1 |
|
|
|
|
||||
|
Res[ f (z), z0 |
=1] = lim (z −1) |
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
= 2. |
||||||||||
|
(z −1)(z |
− |
2) |
2 |
|
|
2 |
|
||||||||||||||||||
|
|
|
|
|
z |
→1 |
|
|
|
|
z→1 (z − 2) |
|
|
|
|
|||||||||||
|
Заметим, что для вычета функции |
f (z) |
относительно про- |
|||||||||||||||||||||||
стого полюса |
z0 =1 можно воспользоваться и формулой (4.35), |
||||||||||||
приняв |
f |
(z) = |
z +1 |
, |
f |
|
(z) = z −1. Тогда |
|
|
|
|||
|
2 |
|
|
|
|||||||||
|
1 |
|
(z −2)2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Res[ f (z), z0 |
|
|
|
z +1 |
|
′ |
|
= 2. |
|||
|
|
= |
1] = |
|
2 |
|
|||||||
|
|
(z − 2) |
/(z −1) |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
z=z0 |
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
По формуле (4.36) при n = 2 имеем
Res[ f (z), z0 = |
|
|
|
d |
|||||
2] = lim |
|
(z |
|||||||
|
|||||||||
|
|
|
|
|
|
z→2 |
dz |
||
= lim |
d z +1 |
|
= lim |
|
− 2 |
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|||||
z→2 |
dz z −1 |
|
z→2 (z −1)2 |
||||||
−2) |
2 |
z +1 |
|
|
= |
|
|
|
|
||
|
(z −1)(z − 2) |
2 |
|||
|
|
|
|
|
= −2.
95
2) Особые точки функции f (z) = z41+1 - нули знаменателя,
то есть корни уравнения z4 +1 = 0. |
|
Так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
4 −1 = 4 cosπ +isinπ = cos π + 2kπ |
+isin |
π + 2kπ |
= |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
cos π +i sin π = ei 4 |
|
|
|
|
|
|
|
|
|
k = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
4 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
3π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
cos |
3π |
|
+i sin |
3π |
|
|
= ei |
|
|
|
k =1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
4 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5π |
|
|
|
5π |
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
+i sin |
= −cos |
−i sin |
= e |
−i |
4 |
|
|
|
|
|
|
|
|
|
|
|
k = 2, |
||||||||||||||||||||||||||||||||||
cos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
4 |
|
4 |
|
|
4 |
4 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
7π |
|
|
|
7π |
|
|
|
|
|
|
|
|
|
3π |
−i sin 3π |
= e−i |
3π |
|
|
|
|
|
||||||||||||||||||||||||||||||
cos |
|
+i sin |
= −cos |
|
|
|
|
|
|
|
|
k = 3, |
|||||||||||||||||||||||||||||||||||||||||
|
|
4 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
4 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
то, применяя формулу (4.35), получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
Res[ f |
2 (z), z0 |
= e |
i |
π |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
e |
−i |
3π |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
4 ] = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
4 |
, |
|
|
|
|
|
||||||||||||||||||||||||
|
|
4z3 |
|
|
|
z0 =ei |
π |
4 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3π |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
9π |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Res[ f |
2 (z), z0 |
= e |
i |
] |
= |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
= |
1 |
e |
−i |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
, |
|
||||||||||||||||||||||||||
|
|
|
|
4z |
3 |
|
|
|
z0 =ei |
3π |
4 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
3π |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
Res[ f |
2 (z), z0 |
= e |
−i |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
e |
i |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
4 ] = |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
4 |
|
|
, |
|
|
|||||||||||||||||||||||||||||||
|
|
|
4z |
3 |
|
|
|
|
|
|
|
π |
4 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z0 =e−i 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9π |
|
|
||||||||||||||||||
|
Res[ f |
2 (z), z0 |
= e |
−i |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
e |
i |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
] = |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 . |
|
|||||||||||||||||||||||||||||||
|
|
|
4z |
3 |
|
|
z0 =e−i |
3π |
4 |
|
|
||||||||||||||||||||||||||||||||||||||||||
3) У функции f (z) = |
|
ez |
−1 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
нули знаменателя: z = 0 и |
||||||||||||||||||||||||||||||||||||||||||||||||||
z(z +1) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
z = −1. Точка z = 0 является устранимой особой точкой, так как
|
|
|
|
|
|
|
z |
|
|
z |
2 |
|
|
z |
3 |
|
|
|
|
|
|
|
|
|
1 |
+ |
|
+ |
|
|
+ |
|
|
+... −1 |
|
||||
|
|
z |
|
|
|
|
|
|
|
|
|
|
|||||||
|
e |
−1 |
|
|
1! |
2! |
|
3! |
|
|
|
||||||||
lim |
|
= lim |
|
|
|
|
= lim |
||||||||||||
z(z +1) |
|
|
|
|
|
z(z +1) |
|
|
|||||||||||
z→0 |
z→0 |
|
|
|
|
|
|
|
z→0 |
||||||||||
Поэтому Res[ f (z), z0 |
= 0] = 0. |
|
|
|
|
|
|
|
|||||||||||
Точка z = −1 - простой полюс:
1+ |
z |
|
+ |
z2 |
+... |
|||
2! |
3! |
|||||||
|
|
|
|
=1. |
||||
|
|
|
z +1 |
|
||||
|
|
|
|
|
||||

96
|
|
|
|
|
e |
z |
−1 |
|
= lim e |
z |
−1 |
|
|
Res[ f (z), z0 |
= −1] = lim (z +1) |
|
|
|
|
=1−e−1. |
|||||||
z(z +1) |
|
z |
|||||||||||
|
z→−1 |
1 |
|
|
|
z→−1 |
|
|
|||||
4) Функция f (z) = z3 sin |
|
имеет особую точку z = 0 , яв- |
|||||||||||
z2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
ляющуюся существенно особой. Действительно, используя известное разложение для sin z по степеням z, легко получить лорановское разложение функции f (z) , содержащее бесконечное
число членов в правой части:
f (z) = z3 z12 − 3!1z6 + 5!1z10 −... = z − 3!1z3 + 5!1z7 −...
Так как член Cz−1 в главной части отсутствует, то коэффици-
ент C−1 = 0. Следовательно, Res[f (z),z=0]=0.
Примеры. Вычислить интегралы, применяя теорию вычетов (заметим, что некоторые из рассмотренных ниже интегралов вычислены с помощью интегральной формулы Коши - см. стр. 6570):
1) ∫ |
z2 |
|
dz. |
||||
z − |
2 |
||||||
|
z |
|
=3 |
|
|||
|
|
|
|||||
Контур интегрирования, особая точка подынтегральной функции и еë расположение относительно контура показаны на рис. 27. В области z < 3 подынтегральная функция аналитична
всюду, кроме точки z0 = 2, являющейся простым полюсом. Cогласно основной теореме о вычетах
|
∫ |
z |
2 |
|
|
|
|
|
|
|
|
z |
2 |
|
|
|
||||
|
|
|
|
|
dz = 2πi Res[ f (z), z0 |
= 2] = 2πi limz→2 |
(z − 2) |
|
|
|
=8πi. |
|||||||||
z −2 |
|
z − |
2 |
|||||||||||||||||
|
z |
=3 |
cos zdz |
|
|
|
|
|
|
|||||||||||
2) |
|
∫ |
|
|
|
. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
z |
2 |
+9 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
z+2i |
|
=3 |
|
|
|
|
|
x2 + ( y + 2)2 = 32 с |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
Контур |
|
интегрирования – |
окружность: |
|||||||||||||||||
центром в точке (0;-2) радиуса r = 3. Подынтегральная функция
cos z |
= |
cos z |
в области |
|
z + 2i |
|
< 3 имеет простой полюс |
|
|
|
|||||||
|
|
|||||||
z2 +9 |
(z +3i)(z −3i) |
|
|
|
|
|
||
|
|
|
|
|
||||
z0 = −3i . Преобразуем интеграл к виду

|
|
|
|
|
|
|
|
|
|
|
97 |
|
|
|
|
|
|
|
|
|
|
|
cos zdz |
|
|
|
|
|
cos zdz |
|
|
|
|
|
cos z |
|
|||
∫ |
= ∫ |
= |
∫ |
|
z −3i |
dz. |
|||||||||||||
|
|
|
|
|
|||||||||||||||
|
2 |
|
|
|
|
||||||||||||||
z+2i |
|
=3 |
z |
|
+9 |
|
|
z+2i |
|
=3 |
(z +3i)(z −3i) |
|
z+2i |
|
=3 |
z +3i |
|||
|
|
|
|
|
|
||||||||||||||
Находим вычет подынтегральной функции по формуле (4.35):
Res[ f (z), z0 = −3i] =
Поэтому |
|
|
|
∫ |
|
|
|
|
cos zdz |
= 2πi |
||||||
|
|
|
|
|
|
|
z |
2 |
+9 |
|
||||||
|
|
|
z+2i |
|
=3 |
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||||
3) |
|
∫ |
|
|
|
|
e2 z |
|
dz . |
|
||||||
|
|
z |
2 |
−5z |
|
|||||||||||
|
z−1 |
|
=5 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|||||||||||
|
|
cos z |
|
|
cos(−3i) |
|
i |
|
||
|
|
z −3i |
|
|
|
= |
= |
ch3. |
||
|
|
|
′ |
|
|
−6i |
6 |
|||
|
(z +3i) |
|
|
|
|
|||||
|
|
|
|
|
z=−3i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
i ch3 = − |
π ch3. |
|
|
|
||||||
6 |
|
|
|
|
3 |
|
|
|
|
|
Контур интегрирования – окружность (x −1)2 + y2 = 25 с центром в точке (1;0). Подынтегральная функция имеет два про-
стых полюса |
z0 |
= 0 и |
z0 = 5, лежащих внутри окружности (см. |
|||||||||||||||||||||||||||||||
рис. 28). По основной теореме о вычетах |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
∫ |
|
e2 z |
|
dz = 2πi{Res[ f (z), z0 = 0] + Re s[ f (z), z0 = 5]}. |
|||||||||||||||||||||||||||||
|
z |
2 |
|
−5z |
||||||||||||||||||||||||||||||
|
z−1 |
|
=5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Применяя формулу (4.35), находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
e |
2z |
, z0 |
|
= |
|
e |
2 z |
|
|
= |
|
e |
2 z |
|
|
= −1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
Res |
|
|
|
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|||||||||||||
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
z |
− |
5z |
|
|
|
(z |
−5z)′ |
|
z=0 |
|
|
2z −5 |
|
z=0 |
5 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
e |
2z |
|
|
|
|
e |
2z |
|
|
|
|
e |
2 z |
|
|
10 |
|
||||||||||
|
Res |
|
|
|
|
, z0 |
= 5 |
= |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
= e . |
|
|||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
z |
− |
5z |
|
|
|
(z |
−5z)′ |
|
z=5 |
|
2z −5 |
|
z=5 |
5 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Заметим, что вычисление вычетов можно выполнить, представляя подынтегральную функцию иначе:
|
|
|
e2z |
, z0 |
|
|
e2z |
|
1 |
|
|
|
= |
|
e2 z |
|
|
|
= − |
1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Res |
|
|
|
|
= 0 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
z |
|
|
−5z |
|
|
z - 5 |
|
z′ |
|
z=0 |
z −5 |
|
z=0 |
5 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
e2z |
, z0 |
|
e2z |
|
|
|
1 |
|
|
|
|
e2 z |
|
|
e10 |
|
||||||||||||||
Res |
|
|
|
|
|
= 5 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
= |
|
|
. |
||
|
2 |
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|||||||||||||
z |
|
|
−5z |
|
|
|
z |
|
(z − |
5) |
|
z=5 |
|
z |
|
z=5 |
5 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
В результате

98
|
|
|
|
|
|
|
|
|
|
|
|
e |
2 z |
dz = 2πi |
− |
1 + e |
|
= |
2π(e −1)i . |
||
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
10 |
|
|
10 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
z−1 |
|
=5 z |
|
−5z |
|
|
|
5 5 |
|
|
5 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4) |
|
∫ |
|
e2 z |
|
dz. |
|
|
|
|
|
|
|
||||||||
(z +1) |
3 |
|
|
|
|
|
|
|
|||||||||||||
|
z |
|
=2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Подынтегральная функция аналитическая всюду в круговой |
|||||||||||||||||||||
области |
|
z |
|
= 2, кроме точки |
z0 |
= −1 - полюса третьего порядка, |
|||||||||||||||
|
|
||||||||||||||||||||
лежащего внутри окружности. Применяя формулу (4.36) при n=3, получим:
|
∫ |
e2 z |
|
dz = 2πiRes[f(z),z |
|
= −1] = 2πi 1 |
lim |
d 2 |
(z +1)3 |
|
e2 z |
|
|
= |
||||
|
|
3 |
0 |
|
2 |
|
|
3 |
|
|||||||||
|
(z +1) |
|
2! |
z→−1 |
dz |
|
|
(z + |
1) |
|
||||||||
|
z |
|
=2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||
=πi lim 4e2 z = 4πi . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
z→−1 |
|
e2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5) |
∫tgzdz. |
|
|
|
|
|
|
|
|
|
|
|
|
|
z=2
Вобласти z < 2 подынтегральная функция tgz аналитична
всюду, кроме точек z = |
π |
и |
z = −π |
, являющихся простыми по- |
|||
|
2 |
|
|
2 |
|
π |
|
люсами. Другие особые точки zn |
= |
+πn функции f (z) = tgz |
|||||
|
|
|
|
|
|
2 |
|
лежат вне области z = 2 и поэтому не учитываются. По формуле
(4.35) имеем
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
sin z |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
Res f (z), z = |
|
|
= |
|
|
|
|
|
|
= −1, |
||||||
|
|
|
|
|
|
|
(cos z)′ |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
z=π |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
sin z |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
Res f (z), z |
= − |
|
|
= |
|
|
|
|
|
= −1. |
|||||||
|
|
|
|
|
|
2 |
(cos z)′ |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z=−π |
||||||
|
|
|
|
|
|
|
∫tgzdz = 2πi(−1−1) = −4πi. |
2 |
|||||||||||||||
Следовательно, |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
z |
|
=2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6) ∫ |
cosπz |
|
dz. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
(z |
2 |
−1) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
z+1 |
|
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||

99
Контур интегрирования – окружность (x +1)2 + y2 =1 с центром в точке (−1;0). Подынтегральная функция имеет две особые точки, являющиеся полюсами второго порядка: z0 =1 и z0 = −1, из которых только полюс z0 = −1 лежит внутри контура интегрирования. Используя формулу (4.36) при n = 2 , находим
|
∫ |
|
cosπz |
|
dz = 2πiRes[f(z), z0 = −1] = |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
(z |
2 |
−1) |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
z+1 |
|
=1 |
|
|
d |
|
|
cosπz |
|
|
d |
|
cosπz |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
= 2πi |
1 |
|
lim |
2 |
|
|
= |
||||||||||||||||||||||
|
|
|
|
|
(z +1) |
|
|
(z +1) |
2 |
(z −1) |
2 == 2πi lim |
|
|
|
|
1) |
2 |
|
|||||||||||
|
|
|
|
|
1! z→−1 dz |
|
|
|
|
z→−1 dz |
(z − |
|
|
|
|
||||||||||||||
|
= 2πi lim |
− |
π sinπz (z |
−1)2 − 2(z −1)cosπz |
|
- |
1 |
|
= − |
πi |
. |
|
|
||||||||||||||||
|
|
|
|
|
(z −1)4 |
|
|
= 2πi |
4 |
|
2 |
|
|
|
|||||||||||||||
|
|
|
|
|
z→−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
7) |
|
|
∫ |
|
|
|
ez |
|
|
dz. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
(z +1)2 (z − 2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
z |
=3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Знаменатель подынтегральной функции обращается в нуль в двух точках z = −1 и z = 2, лежащих внутри окружности z = 3.
Точка z = 2 является простым полюсом, а точка z = −1 - полюсом второго порядка. Применяя основную теорему о вычетах, формулы (4.35) и (4.36) при n = 2 , получим
|
|
|
|
|
|
ez dz |
|
|
|
|
|
|
|
= 2πi{Res[ f (z), z0 |
= 2] + Re s[ f (z), z0 |
= −1]}= |
||||||||||||||||||||||||||||||||||
|
z∫=3 (z −2)(z +1)2 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
e |
z |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
d |
|
|
|
|
2 |
|
|
|
e |
z |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
= |
2πi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
lim |
|
|
(z |
+ |
1) |
|
|
|
|
|
|
|
|
|
= |
||||||||||
(z +1) |
2 |
|
(z − |
|
′ |
|
|
1! |
|
|
|
(z |
+1) |
2 |
(z −2) |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2) |
|
|
|
|
|
|
|
|
|
|
dz |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z=2 |
|
|
|
|
z→−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
2πi |
|
e |
2 |
|
|
|
|
|
|
d |
|
e |
z |
|
|
|
= 2πi |
|
e |
2 |
|
|
|
|
e |
z |
(z −3) |
|
|
|
|
|
|
|
||||||||||||||
= |
|
|
|
+ lim |
|
|
|
|
|
|
|
|
|
|
+ lim |
|
|
= |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
9 |
|
z→−1 dz |
|
− 2 |
|
|
|
|
|
9 |
|
|
|
|
(z −2) |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
z→−1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
4 |
|
|
|
|
|
2π(e |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= |
2πi e |
|
− |
|
|
= |
|
|
− 4) i. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
9e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
9e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Отметим в заключение, что с помощью вычетов удается вычислять многие определенные и несобственные интегралы от функций действительной переменной, для чего эти интегралы предварительно преобразуются в интегралы по замкнутому кон-
туру [1, 3].

100
5. ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
Операционное исчисление представляет собой своеобразный и эффективный метод решения различных математических задач, прежде всего, дифференциальных уравнений. Популяризации операционного исчисления способствовал английский инженер – электротехник О. Хевисайд22, который успешно применил его в электротехнике. В настоящее время операционное исчисление как один из методов так называемых интегральных преобразований широко применяется при решении различных задач физики, механики, автоматики, электротехники, в которых рассматриваются временные процессы. В основе операционного исчисления лежит понятие преобразования Лапласа.
5.1. Преобразование Лапласа
Преобразованием Лапласа называется преобразование, которое ставит в соответствие функции f(t) действительной переменной t функцию F(p) комплексной переменной p по формуле
∞ |
|
F( p) = ∫ f (t)e−pt dt. |
(5.1) |
0 |
|
Несобственный интеграл в правой части формулы (5.1), зависящий от комплексного параметра p, называется интегралом Лапласа.
Интеграл сходится и действительно определяет собой некоторую функцию F(p), если подынтегральная функция f(t) удовлетворяет следующим условиям:
•f(t) - кусочно - непрерывная функция;
•f(t) = 0 при t < 0;
•f(t) по абсолютной величине возрастает не быстрее заранее выбранной показательной функции, то есть можно найти такие постоянные M и α , что f (t) < M eα t . Число α называется
показателем роста функции f(t).
Функция f(t) действительного аргумента t, удовлетворяющая перечисленным выше трем условиям, называется оригиналом , а
22Хевисайд Оливер (18.05.1850 –03.02. 1925) – английский физик
иинженер.
