
ТВиМС / Вероятн_Лекц / Вер_Примитивы / ВерССВ_2_Пр
.doc2.3.4 Ковариационная, дисперсионная, корреляционная
матрицы случайного вектора.
Для многомерного случайного вектора Xn1 парные ковариации между i-ой и j-ой СВ вычисляются по формуле (97), принимающей вид
Kij
=
![]() = E((Xi
– E(Xi))*(Xj
–E(Xj))). (100)
= E((Xi
– E(Xi))*(Xj
–E(Xj))). (100)
Совокупность всех ковариаций (100) вектора Xn1 образует симметричную квадратную матрицу размером (n * n):
KX
=
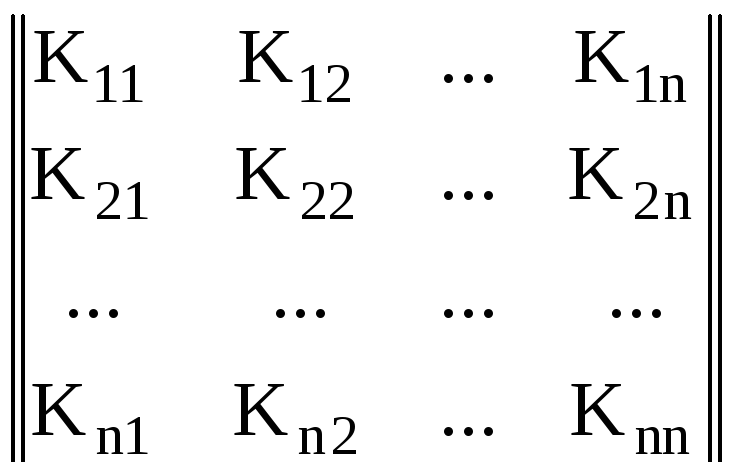 , (101)
, (101)
называемую ковариационной матрицей случайного вектора.
Диагональные элементы матрицы KX представляют собой дисперсии i-ых компонентов:
Kii
=
![]() = D(Xi)
=
= D(Xi)
=
![]() .
.
Если условиться [16], что символ «E» оператора математического ожидания перед именем какой-то матрицы или вектора означает его распространение на каждый элемент такой матрицы, то мы будем вправе пользоваться следующими записями:
E(X1nT)
=![]()
![]() ,
,
![]() ,...,
,...,![]()
![]()
или (для ковариационной матрицы)
KX
= E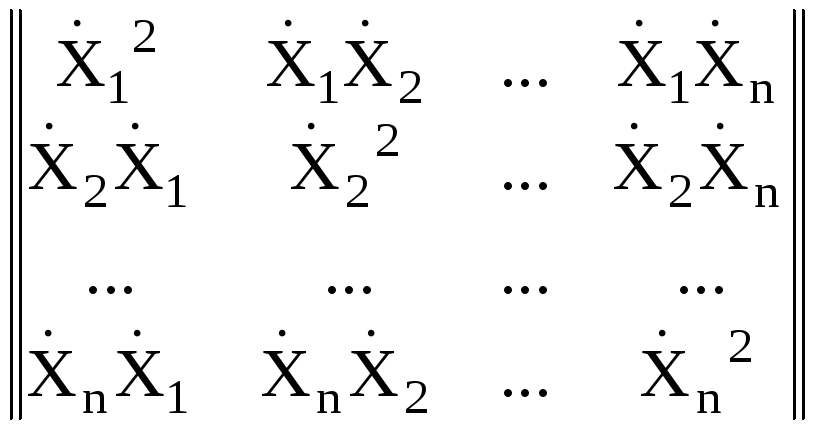 = E
= E![]()
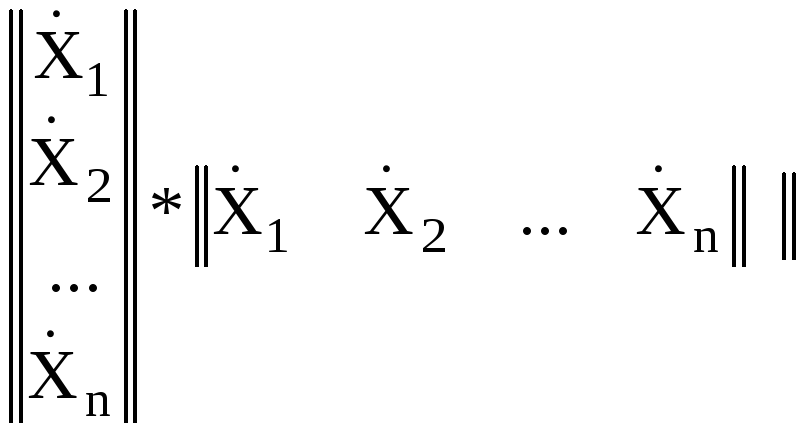
![]()
KX
= E![]() = E
= E![]() (102)
(102)
где верхний индекс «T» – символ транспонирования матрицы.
Когда элементы
ССВ попарно
стохастически не
cвязаны,
то Kij
= 0
![]() (это
было показано в предыдущем параграфе).
В такой ситуации ковариационная матрица
(101) вырождается в дисперсионную:
(это
было показано в предыдущем параграфе).
В такой ситуации ковариационная матрица
(101) вырождается в дисперсионную:
KX
= DX= . (103)
. (103)
Матрица, составленная
из коэффициентов корреляции ρij
, называется корреляционной
и обозначается RX.
Поскольку диагональные коэффициенты
корреляции ρii
![]() 1,
матрица RX
выглядит
следующим образом:
1,
матрица RX
выглядит
следующим образом:
RX= , (104)
, (104)
а ковариационная матрица вектора Xn1, компоненты которого характеризуются постоянными дисперсиями σ2, связана с корреляционной простым соотношением:
KX = σ2 * RX. (105)
Для стохастически
попарно не связанных (попарно
не коррелированных)
компонентов коэффициенты корреляции
ρij
= 0
![]() и ковариационная матрица KX
независимых равноточных компонентов
вырождается в произведение постоянной
дисперсии σ2
на единичную матрицу IX:
и ковариационная матрица KX
независимых равноточных компонентов
вырождается в произведение постоянной
дисперсии σ2
на единичную матрицу IX:
KX
= σ2*IX
=
σ2*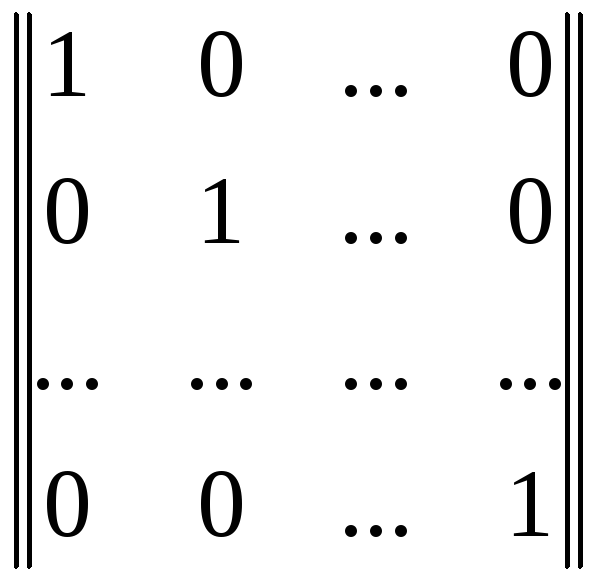 . (106)
. (106)
2.3.5 Функции случайного вектора и их числовые
характеристики.
Функцией случайного вектора называют функцию, аргументы которой являются компонентами ССВ:
z = f(X1, X2, … , Xn) = f(X1nT). (107)
Естественно, что эта функция будет представлять собой одномерную СВ. Она будет иметь свой закон распределения, установление которого не входит в нашу задачу. Ограничимся лишь определением некоторых её ЧХ по соответствующим характеристикам случайных компонентов с учетом вида оператора "f", который полагается детерминированным. Функции, у которых оператор "f" случаен, мы не рассматриваем.
Ниже приводятся несколько теорем о связи ЧХ функции случайных величин с ЧХ её аргументов:
математическое ожидание суммы случайных величин,
математическое ожидание произведения случайных величин,
дисперсия линейной функции случайных величин,
дисперсия произвольной функции случайных величин,
ковариационная матрица линейного преобразования случайного вектора,
ковариационная матрица преобразования случайного вектора.
2.3.5.1 МО суммы случайных величин.
При доказательстве теоремы о МО суммы случайных величин мы, прежде всего, полагаем, что компоненты ССВ, о сумме МО которых идет речь, определены на общем пространстве элементарных событий . Иначе, задача теряет под собой вероятностное обоснование.
Теорема о сумме МО. МО суммы двух СВ, образующих ССВ, равна сумме МО этих СВ. Проведём доказательство на примере дискретной системы двух случайных компонентов.
Дано: Z = f(X; Y) = X + Y; E(X); E(Y).
Доказать: E(X + Y) = E(X) + E(Y).
Доказательство: Опираясь на определение (95) МО функции двумерной ДССВ и определение вероятностей возможных значений компонентов по вероятностям состояний системы (85), выполняем ряд преобразований:
E(X
+ Y)
=![]() =
=
![]() +
+![]() =
=
=
![]() +
+![]() =
=![]() +
+![]() =
+
=
+
![]()
E(X + Y) = E(X) + E(Y). # (108)
Методом математической индукции данное утверждение распространяется на конечную сумму “n” случайных компонентов произвольной ССВ:
E(X1 + X2 +…+ Xn) = E(X1) + E(X2) +...+ E(Xn), (109)
т.е. МО суммы конечного числа случайных величин равно сумме МО этих величин.
2.3.5.2 МО произведения случайных величин.
По-прежнему, мы полагаем, что случайные компоненты определены на общем пространстве (83). Докажем сначала теорему о произведении МО двух СВ, входящих в ССВ.
Теорема о МО произведения двух СВ. МО произведения двух СВ, образующих ССВ, равно произведению МО этих СВ плюс их ковариация.
Дано: Z = f(X,Y) = X * Y; E(X); E(Y); KXY = 11.
Доказать: E(X*Y) = E(X) * E(Y) + KXY.
Доказательство: Раскроем формулу (97), определяющую ковариацию двух СВ, входящих в систему:
KXY = 11 =E(((X – E(X)) * (Y – E(Y))).
Выполнив умножение и учтя только что доказанную теорему о МО суммы СВ, получим следующие результаты:
KXY = E(X*Y – X*E(Y) – Y*E(X) + E(X)*E(Y)) = E(X*Y) – E(X)*E(Y).
Отсюда, окончательно, имеем:
E(X*Y) = E(X)*E(Y) + KXY. # (110)
т.е. МО произведения двух СВ равно произведению МО этих величин плюс их ковариация.
В отличие от первой теоремы, вторая изменяет свой вид, когда случайные сомножители стохастически не связаны попарно (см. 2.3.3):
E(X*Y) = E(X)*E(Y), (111)
т.е. МО произведения двух попарно некоррелированных СВ равно произведению МО этих величин.
Поскольку несвязанность в совокупности влечет за собой попарную несвязанность (см. 2.1.8), то методом математической индукции легко распространить утверждение (111) на “n” стохастически не связанных в совокупности случайных компонентов произвольной ССВ:
E(X1*X2*…*Xn) = E(X1)*E(X2)*...*E(Xn), (112)
т.е. МО произведения стохастически не связанных в совокупности СВ равно произведению МО этих величин.
2.3.5.3 Дисперсия линейной функции СВ.
Две только что доказанные теоремы позволяют вычислять МО суммы или произведения СВ, входящих в систему, по МО слагаемых или сомножителей (с учетом ковариаций стохастически связанных сомножителей), не прибегая к промежуточной операции построения закона распределения результирующей СВ. Третья теорема этой группы даст возможность аналогично решить задачу нахождения дисперсии линейной функции ССВ по коэффициентам этой функции и по ковариационной матрице вектора её случайных аргументов.
Дано:
Z
= C0
+ C1*X1
+ C2*X2
+…+ Cn*Xn
= C0
+
![]() =
=
= C0 + C1n*Xn1 – линейная функция случайного вектора Xn1; KX = {Kij} – ковариационная матрица этого вектора, элементы которой Kij определяются формулой (100).
Найти:
D(Z)
=
![]() –
?
–
?
Решение: По определению дисперсии (51)
![]() =
=
![]() =
=
![]() . (113)
. (113)
Центрированное
значение линейной функции
![]() требуется лишь в качестве промежуточной
величины, необходимой для вывода, т.к.
МО случайных аргументов E(Xi)
не указаны среди известных величин,
хотя они и будут участвовать в
преобразованиях:
требуется лишь в качестве промежуточной
величины, необходимой для вывода, т.к.
МО случайных аргументов E(Xi)
не указаны среди известных величин,
хотя они и будут участвовать в
преобразованиях:
![]() = Z
– E(Z)
=
= Z
– E(Z)
=
![]() -
-
![]() -
-
![]() =
=
=![]() =
=
![]() .
.
Возведем эту величину в квадрат, как этого требует формула (113):
![]() =
=
![]() =
=
![]() .
.
Теперь определим МО этой суммы:
![]() =
=
![]() . (114)
. (114)
Величины
![]() и
и
![]() представляют
собой дисперсии
представляют
собой дисперсии
![]() и ковариации Kij
, соответственно, i-ых
и j-ых
компонентов ССВ и являются диагональными
и недиагональными элементами ковариационной
матрицы KX,
которая известна. Окончательно имеем:
и ковариации Kij
, соответственно, i-ых
и j-ых
компонентов ССВ и являются диагональными
и недиагональными элементами ковариационной
матрицы KX,
которая известна. Окончательно имеем:
![]() =
=
![]() + 2
+ 2![]() .
# (115)
.
# (115)
Для попарно некоррелированных компонентов формула (115) упрощается:
![]() =
=
![]() . (116)
. (116)
Задача 2.13 [4]. Определить границы, в которых находится абсолютное значение коэффициента корреляции XY.
Дано: X и Y – две коррелированные СВ; XY = KXY / (X*Y) – их коэффициент корреляции.
Найти: |ρXY| – ?
Решение: Составим функцию коррелированных случайных аргументов X и Y
Z
= Y
*X
![]() X
*Y
X
*Y
и найдем ее дисперсию по формуле (115):
![]() =
=
![]() *
*![]() +
+![]() *
*![]()
![]() 2
2![]() *
*![]() *
ρXY.
*
ρXY.
Поскольку дисперсия СВ по определению положительна, то справедливо неравенство:
2![]() *
*![]()
![]() 2
2![]() *
*![]() *
*![]() > 0.
> 0.
Разделив его на первое слагаемое левой части, увидим что
1![]()
![]() > 0,
> 0,
откуда получим искомые границы:
|
ρXY
|
![]() 1
1
т.е. абсолютное значение коэффициента корреляции не превышает единицы. #
Теорема (116) имеет следствие: дисперсия алгебраической суммы попарно некоррелированных СВ равна сумме дисперсий этих СВ:
![]() =
=
![]() . (117)
. (117)
