ТВиМС / Вероятн_Лекц / Вер_Примитивы / ВерССВ_1_Пр

2.3 Системы случайных величин.

2.3.1 Основные определения.

Случайная величина, рассмотренная в разделе 2.2, призвана моделировать события, которые могут быть охарактеризованы одним показателем или последовательностью не связанных друг с другом признаков. Если событие имеет более сложную структуру, представляющую собой некоторую систему, то для его описания применяются не отдельные СВ, а системы случайных величин (ССВ) или случайные векторы. Формально переход от одной СВ к ССВ осуществляется простым объединением отдельных СВ в вектор. Однако, при этом, между случайными компонентами такого вектора могут проявиться новые качественные связи, для изучения которых потребуются новые числовые характеристики.

Случайные величины, входящие в систему, удобно обозначать не различными буквами, а одной и той же буквой с нижними индексами. При этих условиях случайный вектор-столбец Х_n1, будет состоять из случайных компонентов X₁ , X₂,…, X_k,…, X_n, каждый из которых обладает своим спектром:

,,…, (k-ый дискретный компонент CСВ),

(k-ый непрерывный компонент CСВ),

где k = 1,2,...,n – индекс случайного компонента, а j – верхний индекс элемента его спектра. Если компоненты – непрерывные СВ, например, X_k, то числа a_k ,b_k – это границы интервала, на котором существуют элементы спектра такого компонента.

Совокупность конкретных значений случайных компонентов описывает определенное состояние ССВ, представляющее собой пересечение состояний этих компонентов:

A_i…s = – (дискретная ССВ),

A_i…s=– (непрерывная ССВ).

Вероятность P(A_i…s) состояния A_i…s может быть определена любым из ранее рассмотренных способов: частотным, классическим, по третьей аксиоме и т.д. При этом важно учесть следующее обстоятельство: для ССВ должно быть построено новое пространство элементарных исходов, являющееся прямым декартовым произведением пространств его компонентов, т.е.

_ _… _n (83)

Связь между возможным состоянием ССВ A_i…s и соответствующей ему вероятностью P(A_i…s) = p_i…s называется законом распределения вероятностей ССВ. Как и в случае с одномерной СВ закон распределения ССВ может иметь аналитическую, табличную или графическую форму. Две последних формы используются лишь для ССВ, содержащих не больше двух компонентов.

Ознакомимся сначала с системой двух дискретных СВ: {X₁; X₂}, в которой, с целью упрощения записей, введем компоненты {X; Y}. Табличная форма закона распределения такой системы представляет собой прямоугольную матрицу распределения, структура которой представлена в таблице (Табл. 2.2).

Матрица распределения двумерной дискретной ССВ. Табл. 2.2

Y X	y1	…	yj	…	yn	= P (X = xi)
x1	p11	…	p1j	…	p1n
…	…	…	…	…	…	…
xi	pi1	…	pij	…	pin
…	…	…	…	…	…	…
xm	pm1	…	pmj	…	pmn
= P (Y = yj)		…		…		[]=[]= =[pij]=1

Состояние двумерной ССВ – это случайная точка:

A_ij = {(X = x_i) (Y = y_j)}

Вероятность наблюдения такого состояния обозначим так:

P(A_ij) = p_ij (84)

Она является первичным элементом матрицы распределения (Табл. 2) и вычисляется любым ранее описанным способом.

В первой колонке и первой строке таблицы размещены элементы спектров обоих случайных компонентов: X и Y. В последней колонке и последней строке находятся вероятности того, что {X = x_i}, а {Y = y_j}, соответственно, определяемые по вероятностям состояний системы:

= и =. (85)

Совокупность всех состояний ССВ заполняет пространство (83):

= ,

причем все состояния попарно несовместны:

.

Следовательно, опираясь на Аксиому 2, получаем:

= = = = = P() = 1 (86)

Для двумерной ССВ вводится понятие функции распределения вероятностей её состояний:

F(x, y) = P(X < x; Y < y). (87)

Для дискретного случая это дает:

F(x, y) = .

Будучи по определению вероятностью, ФР системы двух СВ принадлежит интервалу [0;1], т.е.

.

Свойства ФР системы двух СВ определяются свойствами функций распределения компонентов:

1) F(x_k, y_l) ≥ F(x_i, y_j), если x_k > x_i или y_l > y_j;

2) F(–∞; –∞) = 0;

3) F(∞; ∞) = 1.

Двумерная непрерывная ССВ может быть охарактеризована плотностью распределения вероятностей состояний

f(x,y) = , (88)

которая обладает следующими свойствами:

1) f(x, y) ≥ 0;

2) f(–∞; –∞) = f(∞; ∞) = 0;

3) = 1.

Подынтегральное выражение третьего свойства

f(x, y) dx xy

называется элементом вероятности состояния системы двух СВ. С его помощью можно вычислить вероятность попадания непрерывной двумерной ССВ в некоторую область G пространства :

= . (89)

Отсюда, по правилам интегрального исчисления, можно записать обратную связь между функцией и плотностью распределения двумерной НССВ:

F(x, y) = P(X < x; Y < y) = . (90)

Графические образы для различных форм двумерного закона распределения ССВ ещё существуют в виде поверхностей в трёхмерном пространстве, но их изображения сложны.

2.3.2 Стохастическая несвязанность компонентов ССВ.

Компоненты ССВ – это совместные события, которые могут быть стохастически связанными или не связанными, попарно и/или в совокупности. Условие попарной несвязанности (24) совместных событий для ФР ССВ, представляющей собой вероятность совместного наступления двух состояний (событий!) её компонентов X и Y, примет вид:

F(x, y) = F₁(x) * F₂(y). (91)

C учетом (84) и (85), это условие для двумерной дискретной ССВ запишется так:

= * . (92)

Для непрерывной двумерной ССВ из того же условия (91) получаем:

f(x, y) dx dy = f₁(x) dx * f₂(y) dy,

откуда, окончательно,

f(x, y) = f₁(x) * f₂(y). (93)

Стохастическая несвязанность в совокупности для n-мерной непрерывной ССВ, на основании (25), означает, что ПР ССВ равна произведению ПР случайных компонентов этой системы:

f(x₁, x₂,…,x_n) = f₁(x₁) * f₂(x₂) *...*f_n(x_n). (94)

2.3.3 Моменты ССВ.

Определим математическое ожидание (МО) некоторой функции ССВ на пространстве  (сделаем это и всё последующее изложение материала данного параграфа на примере двумерной ССВ, не теряя той общности, которая нас интересует):

*

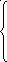= (95)

Для генерализованной характеристики ССВ используются начальные и центральные моменты, в которых в качестве функции φ(x,y) используется произведение r-ой степени компонента X на s-ую степень компонента Y.

Начальный момент порядка "r плюс s"(α _{r s}):

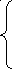
α _{r s} = = (96)

Центральный момент порядка "r плюс s" (μ _{r s}):

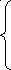
μ _{r s} == (97)

где, как и прежде, , а .

Наиболее часто используются моменты до второго порядка включительно, таблица которых представлена ниже (Табл. 2.3).

Начальные и центральные моменты двумерной ССВ

Табл. 2.3

Порядок rs	Моменты
	Начальные α r s	Центральные μ r s
00 10 01 20 02 11	α 0 0 = 1 α 1 0 = E(X) α 0 1 = E(Y) α 2 0 = E(X2) α 0 2 = E(Y2) α 1 1 = E(X*Y)	μ 0 0 = 1 μ 1 0 = 0 μ 0 1 = 0 μ 2 0 = μ 0 2 = μ 1 1 = α 1 1- α 1 0* α 0 1

Смешанный центральный момент второго порядка ₁₁ = K_XY называют ковариацией или корреляционным моментом. Этот момент служит мерой линейной стохастической связанности компонентов X и Y. Его значение может быть любым: от – ∞ до + ∞, а размерность равна произведению размерностей СВ X и Y. Эти особенности ковариации можно устранить, разделив её на произведение стандартов компонентов:

ρ_XY = K_XY / (_X*_Y). (98)

Величина ρ_XY называется коэффициентом корреляции. Он не имеет размерности и принадлежит отрезку [– 1; 1], т.е. |ρ_XY| 1. Доказательство этому будет дано несколько позже.

Можно установить и обратную связь между коэффициентом корреляции и ковариацией:

K_XY = ρ_XY *_X *_Y. (99)

Когда компоненты ССВ попарно не связаны, то их ковариация и, как следствие, коэффициент корреляции равны нулю. Докажем это на примере двумерной дискретной ССВ.

Дано: {X, Y} = {дискретная ССВ} такая, что p_ij = *;

σ_X ≠ 0 и σ_Y ≠ 0.

Доказать: K_XY = 0 и ρ_XY = 0.

Доказательство: По определению ковариации (97), коэффициента корреляции (98) и условию не связанности компонентов двумерной ССВ (92) имеем:

K_XY = p_ij = =

= = _*= 0 * 0 = 0;

ρ_XY = K_XY / (_X *_Y) = 0 / (_X *_Y) = 0. #

Утверждение доказано. Для НССВ доказательство строится аналогично, см., например,[4].