ТВиМС / Вероятн_Лекц / Вер_Примитивы / ВерССВ_3_Пр

2.3.5.4 Дисперсия произвольной функции СВ.

Для произвольной функции СВ

Z = f(X₁, X₂, …, X_n) (118)

связь между ее дисперсией и элементами ковариационной матрицы K_X случайных аргументов может быть установлена лишь приближенно. Однако, при малых по модулю центрированных значениях случайных аргументов (в геодезии это величины, модуль которых порядка 10^-4 и меньше) степень такого приближения вполне удовлетворительна.

Дано: Z = f(X₁, X₂, …, X_n) – произвольная функция случайного вектора X_n1; K_X= {K_ij} – ковариационная матрица этого вектора, элементы которой K_ij определяются формулой (100).

Найти: D(Z) = – ?

Решение: Представим в формуле (118) каждую СВ X_i в виде суммы ее МО и соответствующего центрированного значения :

.

Разложим её в ряд Тейлора в окрестности точки E(X_1n^T), ограничиваясь только линейными членами:

+ ()*+...+ () *. (119)

Отсюда сразу следует, что

, (120)

так как =μ₁ 0.

Центрированное значение величины Z будет линейной функцией центрированных значений её аргументов :

= Z – E(Z) *+…+ () *. (121)

Численные значения частных производных () находят в окрестности точки разложения E(X_1n^T), где и вычисляется искомая дисперсия.

Окончательно, применяя к функции (121) формулу (115) и учитывая, что по третьему свойству дисперсии (60)

= ,

имеем:

=+2. # (122)

Полученная формула упрощается для попарно некоррелированных аргументов:

=. (123)

2.3.5.5 Определение дисперсий некоррелированных аргументов по дисперсии функции этих аргументов.

Сформулированная в заголовке данного параграфа задача имеет множество решений, так как в одном уравнении (123) мы имеем «n K_ij» неизвестных. Для выбора единственного решения требуются дополнительные ограничения, удовлетворяющие нас по каким-либо мотивам. Во-первых, очевидно, что все решения должны быть положительными, т.е. они не должны противоречить определению дисперсии. Во-вторых, ограничения можно сформулировать, опираясь на здравый смысл. Рассмотрим два наиболее простых и практически обоснованных варианта ограничений: «принцип равных дисперсий», «принцип равных влияний» и «принцип имеющихся возможностей».

Принцип равных дисперсий. Данный принцип используется в ситуации, когда аргументы X_i являются физически однородными величинами и для их измерений предполагается использование однотипной технологии, характеризующейся постоянной дисперсией:

= = ². (124)

С учетом последнего ограничения, формула (123) упрощается:

=².

Откуда, окончательно, получаем выражение для искомой постоянной дисперсии аргументов:

²=/. (125)

Принцип равных влияний. Этот принцип используется в случае физически неоднородных аргументов и довольно условен. Под «влиянием» отдельного аргумента понимается произведение квадрата его частной производной на дисперсию этого аргумента, а сам принцип равных влияний заключается в приравнивании таких произведений друг другу:

= . (126)

Данное условие приводит к тому, что в формуле (123) оператор суммы  заменяется множителем, равным числу аргументов «n» :

. (127)

Из формулы (127) получаем «n» значений искомых дисперсий:

. (128)

Принцип имеющихся возможностей. Этот принцип предполагает, что имеется возможность нахождения значений части случайных аргументов X_j с дисперсиями , определяемая, например, парком измерительных приборов. Не теряя общности, мы можем положить, что это – k первых аргументов. Дисперсии остальных n – k аргументов X_i необходимо найти. Сказанное позволяет разбить сумму (123) на две составляющие:

= + = +. (129)

Имея возможность вычислить первую сумму

= ,

найдем вторую:

= – . (130)

Далее мы можем столкнуться с двумя ситуациями:

а) 0 и б) > 0.

В первом случае решения не существует, так как имеющиеся возможности определения величин X_j приводят к превышению заданного предельного значения дисперсии функции . Выхода здесь два: либо изменить проект определения величины Z, моделируемый функцией (118), либо искать новые возможности (приборы, технологии), характеризующиеся мèньшими дисперсиями .

Во втором случае решение находят, используя уже описанный выше принцип равных дисперсий (125) или принцип равных влияний (128).

2.3.5.6 Ковариационная матрица линейного преобразования

случайного вектора.

Следующая теорема данного цикла расширяет наши возможности на случай, когда исследуется не одна функция случайного вектора, а целая линейная вектор-функция случайного вектора:

Y_m1 = C_mn * X_n1, (131)

ковариационная матрица которого K_X – известна. Представим эту теорему в форме задачи по нахождению ковариационной матрицы линейного преобразования случайного вектора.

Дано: Y_m1 = C_mn * X_n1 – линейное преобразование вектора X_n1; K_X={K_ij} – ковариационная матрица преобразуемого вектора, элементы которой K_ij определяются формулой (100).

Найти: Ковариационную матрицу K_Y – ?

Решение: Опираясь на матричное определение (102) ковариационной матрицы произвольного случайного вектора, можем написать:

K_Y = E{(Y_m1 – E(Y_m1)) * (Y_m1 – E(Y_m1))^T}. (132)

Подставив в (132) вместо вектора Y_m1 его зависимость (131) от вектора X_n1 и опустив индексы, получим такой результат:

K_Y = E((CX – E(CX)) * (CX – E(CX))^T) =

= E(C*(X – E(X)) * (X – E(X))^T * C^T) =

= C * E((X – E(X)) * (X – E(X))^T) * C^T.

Поскольку E((X – E(X)) * (X – E(X))^T) = K_X, окончательно записываем:

K_Y = C * K_X * C^T. # (133)

В качестве Упражнения 2.3 докажите, что формула (115) – это частный случай (133), когда m = 1.

Задача 2.14 Два смежных угла y₁ и y₂ вычислены как разности соседних некоррелированных и равноточно измеренных направлений x₁, x₂ и x₃, т.е. y₁ = x₂ – x₁ и y₂ = x₃ – x₂. Найти коэффициент корреляции этих углов.

Дано: Y₂₁^T = ; X₃₁^T = ; K_X = σ²*I₃₃, т.к. измерения некоррелированные (K_ij= 0 ) и равноточные ( = σ²), где σ² – дисперсия направлений.

Найти: = ρ₁₂ – ?

Решение: Вектор углов Y₂₁ является линейным преобразованием вектора направлений X₃₁. Матрица преобразования C₂₃ находится по связям, описанным в тексте задачи:

C₂₃ = .

Окончательно, преобразование принимает вид:

= * .

Формула (133) позволяет найти ковариационную матрицу углов:

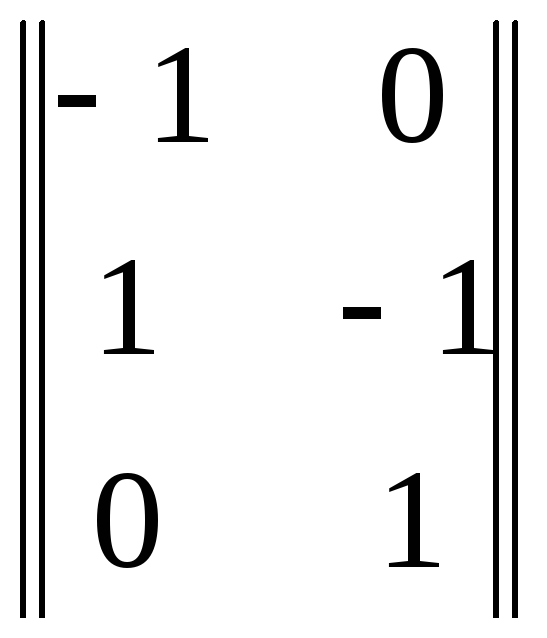K_Y = σ² * = σ² = .

На основании соотношения (99), с одной стороны,

K₁₂ = ρ₁₂ * σ₁*σ₂,

где = K₁₁ = = K₂₂ = σ², а с другой стороны:

K₁₂ = – σ².

Таким образом,

K₁₂ = ρ₁₂ * σ₁ * σ₂ = ρ₁₂ * 2 σ² = – σ².

Отсюда легко определяется искомый коэффициент корреляции смежных углов:

ρ₁₂ = – σ²/ 2 σ² = – 0,5.

2.3.5.7 Ковариационная матрица произвольного

преобразования случайного вектора.

Произвольное преобразование F_m1 случайного вектора X_n1, характеризующегося ковариационной матрицей K_X, в новый случайный вектор Y_m1 будет иметь свою ковариационную матрицу K_Y. Найдем ее.

Дано: Y_m1 = F_m1(X_n1) – произвольное преобразование; K_X – ковариационная матрица аргументов.

Найти: K_Y – ?

Решение: По определению (102) вновь имеем

K_Y = E{(Y_m1 – E(Y_m1)) * (Y_m1 – E(Y_m1))^T}. (134)

Разложим в ряд Тейлора вектор-функцию Y_m1 = F_m1(X_n1) в окрестности точки E(X_n1), ограничиваясь линейными членами и учитывая, что X_n1=E(X_n1) +, получаем:

Y_m1 = F_m1(E(X_n1) +)F_m1(E(X_n1)) + {F/X}_mn*, (135)

где, согласно [7], {F/X}_mn = f_mn – дифференциальный оператор, представляющий собой матрицу частных производных, в каждой из m строк которой стоят n частных производных по каждому из аргументов.

Найдем теперь МО этой функции:

E(Y_m1)E(F_mn(E(X_n1)) + f_mn*) = F_mn(E(X_n1)) + f_mn*E())

E(Y_m1) F(E(X_n1)), (136)

т.к. E() = 0, как вектор центральных моментов первого порядка.

Вычитая из (135) выражение (136), находим центрированный вектор

= Y_m1 – E(Y_m1) f_mn * (137)

и, используя определение (102), находим интересующую нас ковариационную матрицу K_Y произвольного преобразования случайного вектора X_n1:

K_Y=E(}E(f_mn** * f_nm^T) = f_mn* E() * f_nm^T.

K_Y = f_mn*K_X*f_nm^T # (138)

Это и есть искомая приближенная связь между ковариационной матрицей K_X случайного вектора X_n1 и ковариационной матрицей K_Y его произвольного преобразования Y_m1 = F_m1(X_n1).

Доказать в качестве Упражнения 2.4, что формула (122) является частным случаем соотношения (138), когда m = 1.

Задача 2.14 Приращения прямоугольных координат геодезического пункта Δx и Δy вычислены по независимым аргументам: расстоянию s и дирекционному углу . Полагая известными стандарты аргументов σ_s и σ_α, найти ковариационную матрицу приращений координат K_X и установить, при каких относительных значениях стандартов измерений эти приращения будут некоррелированны.

Дано: Δx = s * cos; Δy = s * sin; σ_s; σ_α.

Найти: а) K_X – ?;

б) соотношение между σ_s и σ_α, при котором K_xy = 0.

Решение: Запишем, прежде всего, нелинейное преобразование расстояния s и дирекционного угла  в приращения координат Δx и Δy в матричном виде:

= .

Составим матрицу частных производных приращений координат Δx и Δy по расстоянию s и углу :

f₂₂ = = .

Ковариационная матрица аргументов, как это следует из условий задачи, будет диагональной:

K_s, = .

Теперь мы можем найти ковариационную матрицу K_X приращений координат, выполнив преобразования по формуле (138):

K_X ==**=

=.

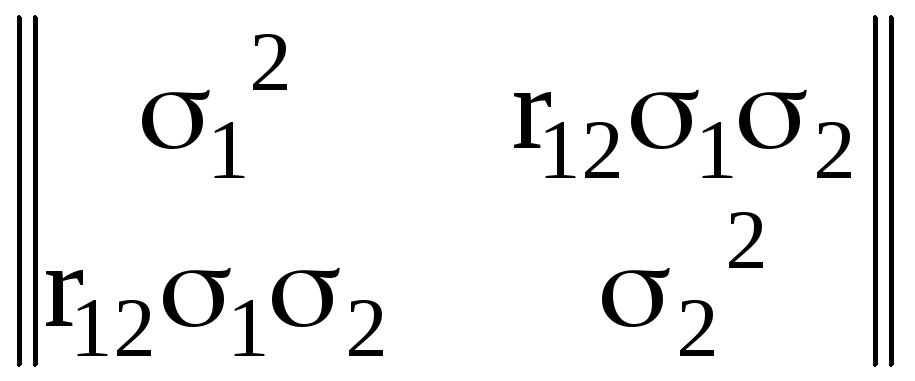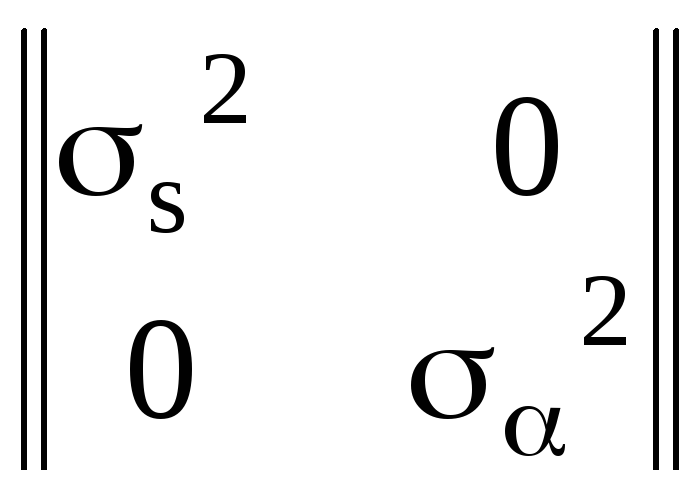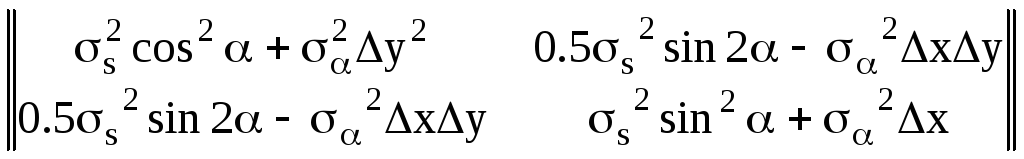Это – ответ на первый вопрос задачи. Что же касается ответа на второй вопрос, то для его получения необходимо приравнять нулю элемент K₁₂ только что полученной матрицы:

0.5* sin2α – * Δx Δy = 0,

а затем, заменить в нем приращения координат их выражениями через расстояние s и дирекционный угол :

0.5* sin2α = 0.5* s² * sin2α.

Отсюда мы сразу находим искомое соотношение между стандартами линии и дирекционного угла, при котором приращения абсциссы Δx и ординаты Δy не будут коррелированны:

σ_s / s = σ_α,

т.е. относительный стандарт линии должен равняться стандарту дирекционного угла, выраженному в радианной мере.

Отметим, что при этих условиях и сами стандарты приращений = и = упростятся и будут равными друг другу и стандарту линии:

₁ = ₂ = _s.

Убедитесь в этом в качестве Упражнения 2.5.