
MetodTM1
.pdfТаким образом, абсолютное ускорение точки в сложном движении при
поступательном переносном движении по прямой можно представить в виде
r |
r |
r |
r |
векторного равенства a |
= arτ + arn + aeτ . |
||
3.2. Задание К4. Определение скорости и ускорения точки при сложном движении
Задание включает две задачи с вращательным и поступательным видами переносного движения точки.
Задача 1. Вращение тела относительно неподвижной оси задается зако-
ном изменения угла поворота: ϕe = ϕe (t) или законом изменения его угловой скорости: ωe = ωe (t). Движение точки относительно тела отсчитывается от её начального положения в точке С и задается законом изменения длины дуги ок-
ружности или отрезка прямой линии: CM = Sr = Sr (t).
Определить абсолютные скорость и ускорение точки в заданный момент времени t1.
Задача 2. Поступательное движение тела, несущего точку, задается зако-
ном изменения координаты xe = xe (t) . Движение точки относительно тела от-
считывается от её начального положения в точке С и задается законом измене-
ния длины дуги окружности или отрезка прямой линии: CM = yr = yr (t).
Определить абсолютные скорость и ускорение точки в момент времени t2 , который либо задаётся в исходных данных задачи, либо на схеме описаны условия, из которых он находится.
Номера вариантов заданий даны на рис. 3.2 – 3.5.
Варианты исходных данных приведены в табл. 3.1.
60
|
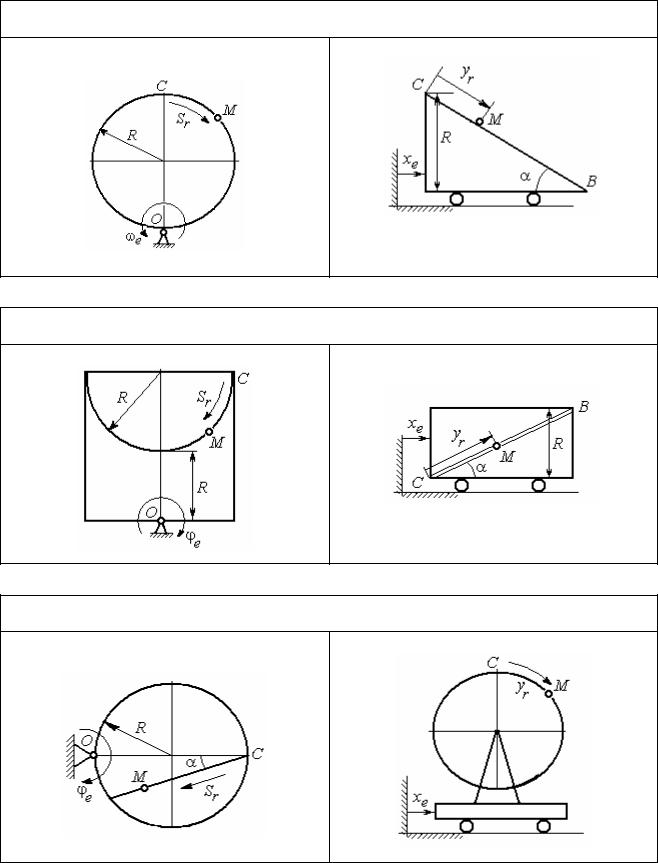
Варианты № 1, 11, 21 |
Задача 1 |
Задача 2 |
В момент t = t2 точка М прошла половину пути СВ
|
Варианты № 2, 12, 22 |
Задача 1 |
Задача 2 |
В момент t = t2 точка М прошла 2/3 пути СВ
|
Варианты № 3, 13, 23 |
Задача 1 |
Задача 2 |
Рис. 3.2. Задание К4. Сложное движение точки. Номера вариантов задания 1 – 3, 11 – 13, 21 – 23
61
|
|
Продолжение вариантов задания К4 |
|
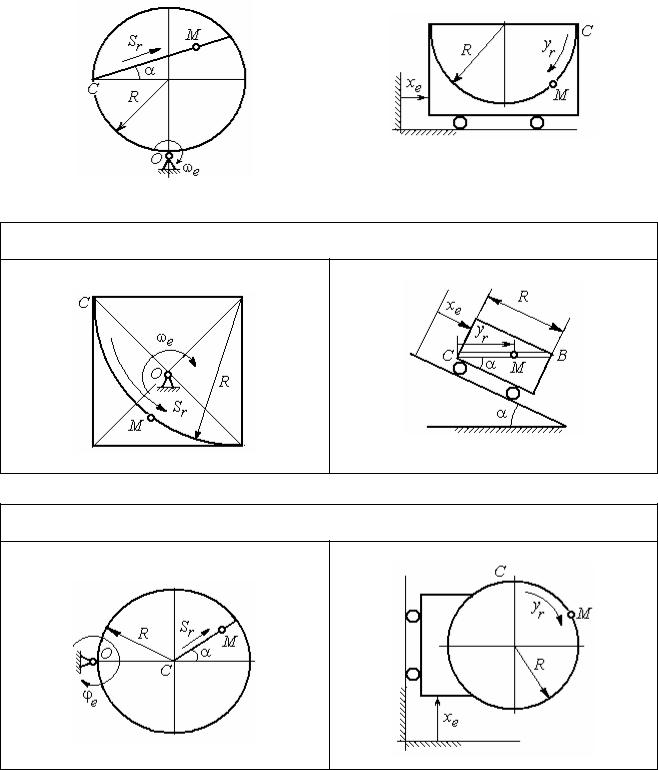
Варианты № 4, 14, 24 |
|
|
|
|
Задача 1 |
|
Задача 2 |
|
|
|
|
Варианты № 5, 15, 25 |
Задача 1 |
Задача 2 |
В момент t = t2 точка М прошла путь СВ
|
Варианты № 6, 16, 26 |
Задача 1 |
Задача 2 |
Рис. 3.3. Задание К4. Сложное движение точки. Номера вариантов задания 4 – 6, 14 – 16, 24 – 26
62
|
Продолжение вариантов задания К4 |
|
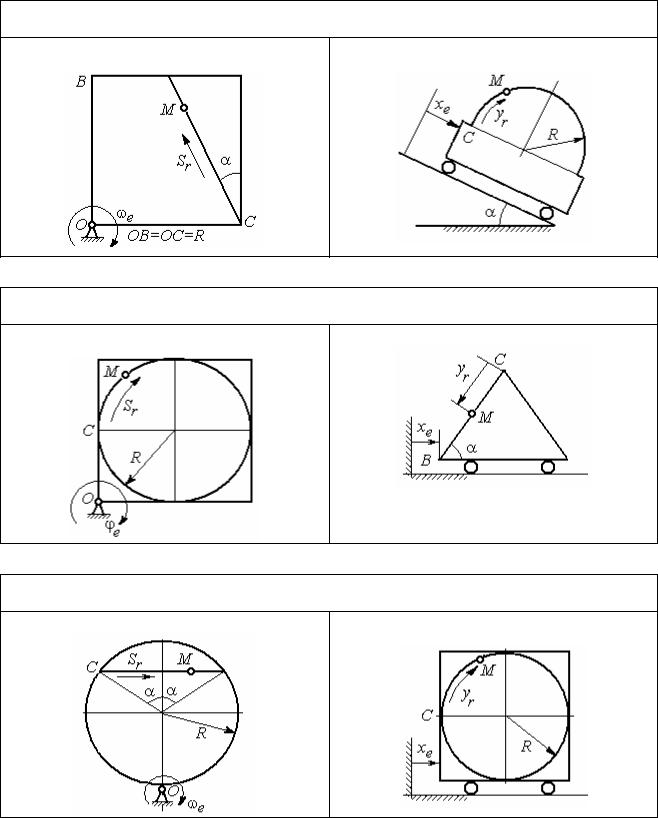
Варианты № 7, 17, 27 |
Задача 1 |
Задача 2 |
|
Варианты № 8, 18, 28 |
Задача 1 |
Задача 2 |
В момент t = t2 точка М прошла половину пути СВ = R
|
Варианты № 9, 19, 29 |
Задача 1 |
Задача 2 |
Рис. 3.4. Задание К4. Сложное движение точки. Номера вариантов задания 7 – 9, 17 – 19, 27 – 29
63
|
Окончание вариантов задания К4 |
|
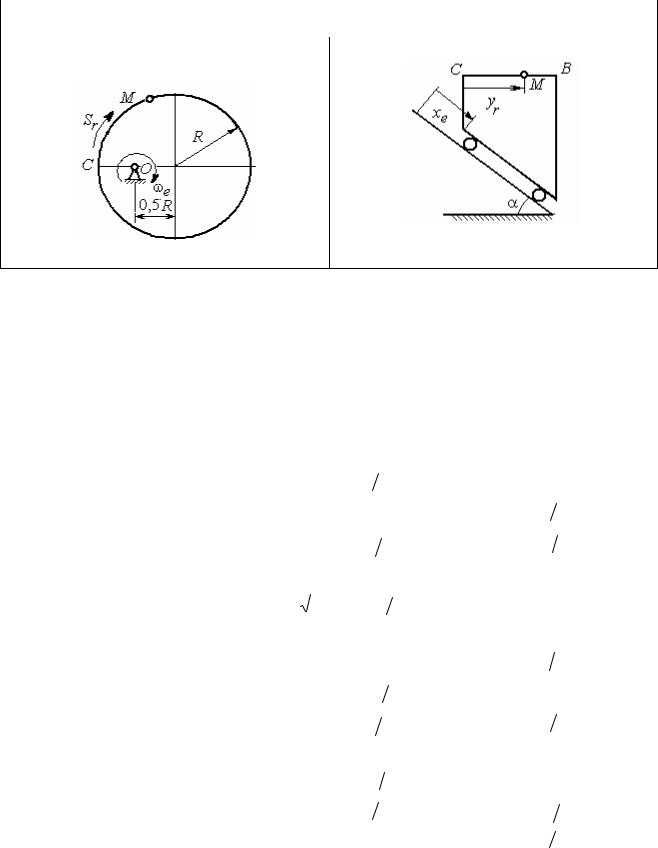
Варианты № 10, 20, 30 |
|
|
Задача 1 |
Задача 2 |
В момент t = t2 точка М прошла половину пути СВ = R
Рис. 3.5. Задание К4. Сложное движение точки. Номера вариантов задания 10, 20, 30
Таблица 3.1
Исходные данные для заданий по сложному движению точки
Номер |
Номер |
R , |
α , |
CM = S |
r |
(t) , см |
ϕ |
e |
(t) , рад; ω (t) , рад/с |
t1, c |
||||
варианта |
задачи |
|
|
|
|
|
|
e |
|
t2, c |
||||
задания |
см |
град |
CM = yr (t) , см |
|
|
xe (t) , см |
|
|||||||
1 |
1 |
3 |
– |
Sr = 2πsin(πt |
6) |
|
|
ωe = 4t2 |
|
1 |
||||
2 |
4 |
30 |
yr = 4t 2 |
|
|
|
xe = 2cos(πt |
6) |
– |
|||||
|
|
|
|
|||||||||||
2 |
1 |
2 |
– |
Sr = 4πsin2 (πt |
6) |
|
|
ϕe = 6cos(πt |
3) |
1 |
||||
2 |
3 |
60 |
yr =t2 + t |
|
|
|
xe = 1+ cos(πt) |
– |
||||||
|
|
|
|
|||||||||||
|
1 |
4 |
30 |
Sr = 2 |
|
[t + sin(πt 2)] |
|
|
ϕe = 4t − t2 |
|
1 |
|||
3 |
3 |
|
|
|
||||||||||
2 |
6 |
– |
yr = π[2t + sinπt] |
|
|
xe =5t − t 2 |
|
1 |
||||||
4 |
1 |
4 |
60 |
Sr = 2(t3 + t) |
|
|
ωe =6cos(πt |
6) |
1 |
|||||
2 |
3 |
– |
yr = π[2t + cos(πt 2)] |
|
|
xe =t3 − 4t |
|
1 |
||||||
|
|
|
|
|||||||||||
5 |
1 |
6 |
– |
Sr = 4πsin2 (πt |
6) |
|
|
ωe = 6cos(πt |
3) |
1 |
||||
2 |
2 |
30 |
yr = t2 + 2t |
|
|
|
xe = t2 − 4t |
|
– |
|||||
|
|
|
|
|
||||||||||
6 |
1 |
6 |
60 |
Sr =t +10sin(πt |
6) |
|
|
ϕe = 2t2 − 5t |
1 |
|||||
2 |
3 |
– |
yr = 4πsin(πt |
6) |
|
|
xe =[1− cos(πt |
4)] |
1 |
|||||
|
|
|
||||||||||||
7 |
1 |
8 |
30 |
Sr = 2(t3 + 3t) |
|
|
ωe = 6cos(πt |
6) |
1 |
|||||
2 |
4 |
30 |
yr = 2πt2 |
|
|
|
xe =t3 − 5t |
|
1 |
|||||
|
|
|
|
|
||||||||||
64
|
|
|
|
|
|
|
|
|
|
|
|
|
Продолжение табл. 3.1 |
|||
Номер |
Номер |
R , |
α , |
CM = S |
r |
(t) , см |
ϕ |
e |
(t) , рад; ω (t) , рад/с |
t1, c |
||||||
варианта |
задачи |
|
|
|
|
|
|
|
|
e |
|
t2, c |
||||
задания |
см |
град |
CM = yr (t) , см |
|
|
|
xe (t) , см |
|||||||||
8 |
1 |
8 |
– |
Sr = 2π[t2 + sinπt] |
|
|
ϕe =t2 − 5t |
2 |
||||||||
2 |
6 |
30 |
yr = t(t +1) |
|
|
|
|
|
xe = cosπt |
– |
||||||
|
|
|
|
|
|
|||||||||||
9 |
1 |
8 |
30 |
|
Sr = 2t2 |
|
|
|
|
ωe = cos(πt |
8) |
2 |
||||
2 |
3 |
– |
yr = 4πsin2 (πt |
4) |
|
|
xe =(3 − 2t)2 |
1 |
||||||||
10 |
1 |
6 |
– |
Sr = π(2t3 + sinπt) |
|
|
ωe =5t − 2t3 |
1 |
||||||||
2 |
4 |
30 |
yr = t2 + 2t |
|
|
|
|
xe = 1+ cosπt |
– |
|||||||
|
|
|
|
|
||||||||||||
|
1 |
6 |
– |
Sr =8πsin(πt 12) |
|
|
ω = 2 + cos(πt 4) |
2 |
||||||||
11 |
2 |
6 |
|
yr = 4sinπt |
|
|
|
|
e |
|
|
|
||||
60 |
|
|
|
|
xe = t2 − 2t |
– |
||||||||||
|
|
|
|
|
||||||||||||
12 |
1 |
18 |
– |
Sr = π(2t2 + 2t) |
|
|
ϕe (t) = 3t − t2 |
2 |
||||||||
2 |
6 |
30 |
yr = 2t2 + t |
|
|
|
|
xe |
= 1+ cos(πt) |
– |
||||||
|
|
|
|
|
||||||||||||
13 |
1 |
10 |
60 |
Sr = t3 + t |
|
|
|
|
ϕe =6cos(πt |
6) |
2 |
|||||
2 |
6 |
– |
yr = 6cos(πt 3) |
|
|
xe = t(t +1) |
1 |
|||||||||
|
|
|
||||||||||||||
14 |
1 |
4 |
30 |
Sr = 8 3sin(πt 12) |
|
|
ωe =(3 − 2t)2 |
2 |
||||||||
2 |
3 |
– |
yr = 2πsin(πt |
6) |
|
|
xe = 2t2 − 5t |
1 |
||||||||
|
|
|
||||||||||||||
15 |
1 |
8 |
– |
Sr = 4πsin2 (πt |
4) |
|
|
ωe = 2 + cos(πt 4) |
1 |
|||||||
2 |
5 |
60 |
yr = 5t + t2 |
|
|
|
xe = cos(πt |
6) |
– |
|||||||
|
|
|
|
|||||||||||||
16 |
1 |
12 |
90 |
Sr = 3[t + sin(πt |
2)] |
|
|
ϕe = 2t − 3t2 |
1 |
|||||||
2 |
15 |
– |
yr |
= π(4t + t2 ) |
|
|
|
xe = 6sin(πt 3) |
1 |
|||||||
|
|
|
|
|||||||||||||
17 |
1 |
6 |
45 |
Sr =3 |
2[t |
2 |
+ 2sinπt] |
|
|
ωe (t) = 4t2 − 6 |
1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
6 |
60 |
yr = 8πsin(πt 12) |
|
|
xe = |
2 sin(πt 8) |
2 |
|||||||
18 |
1 |
8 |
– |
Sr = 4π |
2 sin(πt |
8) |
|
|
ϕe =18t − 4t2 |
2 |
||||||
2 |
8 |
60 |
yr |
= 3t + 2t 2 |
|
|
|
xe = sinπt |
– |
|||||||
|
|
|
|
|||||||||||||
19 |
1 |
8 |
60 |
Sr = 2 |
3[t + sin(πt |
2)] |
|
|
ωe =5t − t |
2 |
1 |
|||||
|
|
|
|
|||||||||||||
2 |
9 |
– |
yr = 6πcos(πt 3) |
|
|
xe = cos(πt |
6) |
1 |
||||||||
|
|
|
||||||||||||||
20 |
1 |
4 |
– |
Sr = 4πsin(πt |
6) |
|
|
ωe =3t − 5 |
1 |
|||||||
2 |
6 |
60 |
yr |
= 3t + 2t 2 |
|
|
|
xe = πsinπt |
– |
|||||||
21 |
1 |
3 |
– |
Sr = 4π |
2 sin(πt |
8) |
|
|
ωe = 6t −14 |
2 |
||||||
2 |
8 |
45 |
yr |
=(t2 + 3t) |
|
|
|
xe =t + 2sinπt |
– |
|||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
65 |
|
|
|
|
|
|
|
|
||

Окончание табл. 3.1
Номер |
Номер |
R , |
α , |
CM = S |
r |
(t) , см |
ϕ |
e |
(t) , рад; ω (t) , рад/с |
t1, c |
|||||||
варианта |
задачи |
|
|
|
|
|
|
|
e |
|
|
t2, c |
|||||
задания |
см |
град |
CM = yr (t) , см |
|
|
xe (t) , см |
|
|
|||||||||
22 |
1 |
4 |
– |
Sr = 2π(t2 + 2t) |
|
|
ϕe = 6cos(πt |
|
6) |
1 |
|||||||
2 |
9 |
60 |
yr =8sinπt |
|
|
xe = 5t − t2 |
|
– |
|||||||||
|
|
|
|
||||||||||||||
23 |
1 |
6 |
45 |
Sr =12sin(πt 8) |
|
|
ϕe =t2 + cos(πt |
4) |
2 |
||||||||
2 |
6 |
– |
yr =6π[t + sin(πt 6)] |
|
|
xe = 5t − t2 |
|
1 |
|||||||||
|
|
|
|
||||||||||||||
24 |
1 |
6 |
45 |
Sr =12sin(πt 8) |
|
|
ωe =t + 4cos(πt |
4) |
2 |
||||||||
2 |
6 |
– |
yr = π(t2 + 2t) |
|
|
xe =6cos(πt |
6) |
1 |
|||||||||
25 |
1 |
6 |
– |
Sr = 2πt2 |
|
|
ωe =3sin(πt |
3) |
1 |
||||||||
2 |
4 |
45 |
yr = 2t(t + 3t) |
|
|
xe = 2(t3 − 3t) |
– |
||||||||||
|
|
|
|||||||||||||||
26 |
1 |
6 |
120 |
Sr =t2 + t |
|
|
ϕe =12cos(πt 12) |
2 |
|||||||||
2 |
9 |
– |
|
|
|
|
|
|
|
|
|
xe = 2(t2 − 3t) |
1 |
||||
yr = π |
|
3sin(πt 3) |
|
|
|||||||||||||
|
|
|
|
||||||||||||||
|
1 |
10 |
60 |
Sr = |
|
|
|
|
|
|
|
|
ωe = 6cos(πt |
6) |
2 |
||
27 |
|
3(t2 + t) |
|
|
|||||||||||||
2 |
9 |
30 |
|
|
|
|
|
|
|
|
|
xe =t + 4cos(πt |
4) |
1 |
|||
yr = |
3πsin(πt 3) |
|
|
||||||||||||||
|
|
|
|||||||||||||||
28 |
1 |
2 |
– |
Sr =6πsin(πt 6) |
|
|
ϕe = 2t + cos(πt |
2) |
1 |
||||||||
2 |
6 |
|
yr = 2t + 3t2 |
|
|
xe = |
t + sinπt |
– |
|||||||||
29 |
1 |
8 |
30 |
Sr =(t2 + 2t) |
|
|
ωe =6sin(πt 12) |
2 |
|||||||||
2 |
3 |
– |
|
|
|
|
|
|
|
|
|
xe = 5t − t2 |
|
1 |
|||
yr = 2π |
|
|
3sin(πt 3) |
|
|
|
|||||||||||
|
|
|
|
|
|
||||||||||||
30 |
1 |
2 |
– |
π(t2 + 2t) |
|
|
ωe (t) =6cos(πt |
6) |
1 |
||||||||
2 |
3 |
60 |
yr |
= t + t2 |
|
|
xe = |
t + sinπt |
– |
||||||||
|
|
|
|||||||||||||||
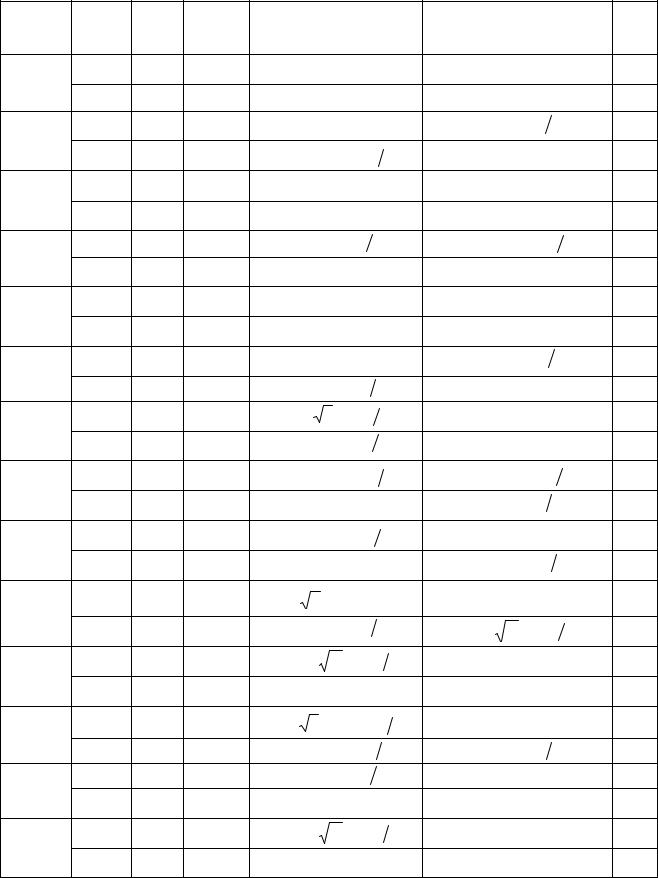
Пример выполнения задания К4. Сложное движение точки
Задача 1. Фигура, состоящая из половины диска и равнобедренного тре-
|
угольника (рис. 3.6), вращается вокруг оси, пер- |
||
|
пендикулярной плоскости фигуры и проходящей |
||
|
через вершину А треугольника. Вращательное |
||
|
движение задается законом изменения угла по- |
||
Рис. 3.6. Схема |
ворота фигуры ϕ |
e |
= 5t − 2t2 рад. Положительное |
|
|
||
сложного движения точки |
направление вращения отмечено на схеме дуго- |
|
66
вой стрелкой ϕe . По ободу диска от точки В движется точка М. Движение точ-
ки относительно диска задается законом изменения длины дуги окружности:
BM = Sr = 9πt2 см. Положительное направление движения точки М на рис. 3.6
показано дуговой стрелкой Sr . Радиус диска R = 9 см.
Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t1 = 1 с.
Решение
Вращение фигуры будет для точки М переносным движением. Относи-
тельное движение точки М – её движение по окружности обода диска.
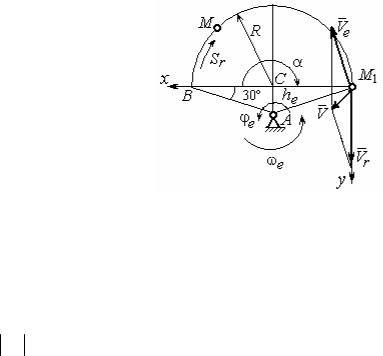
Для определения положения точки М на ободе диска вычислим расстоя-
ние, которое она прошла на заданный момент |
|
|||||
времени. Длина дуги окружности, пройденной |
|
|||||
точкой за 1 с, составляет Sr (1) = 9π см. Поло- |
|
|||||
жение точки М определяется центральным уг- |
|
|||||
лом α = |
Sr (1) |
= |
9π |
= π . Положение |
точки в |
|
R |
|
|
||||
|
9 |
|
|
|
||
момент времени t1 = 1 с отмечено на |
рис. 3.7 |
Рис. 3.7. Расчетная схема |
||||
точкой М1. |
|
|
|
|
для вычисления абсолютной |
|
|
|
|
|
скорости точки при сложном |
||
Для определения скорости переносного |
движении |
|
движения точки вычисляем значение производной: ϕ& e = 5 − 4t . Угловая ско-
рость вращения фигуры: ωe = ϕ& e . При t1 = 1 с ϕ& e (1) = 1 рад/с. Положительная величина производной ϕ& e (1) показывает, что вращение фигуры в данный мо-
мент происходит в положительном направлении, что отмечено дуговой стрел-
кой ωe на рис. 3.7.
В момент времени t1 = 1 с точка М находится в положении М1. Скорость
Ve переносного движения точки в момент времени t1 = 1 с Ve (1) = ωe (1)he , где
67

R
расстояние от точки М1 до оси вращения фигуры he = AM1 = cos30o = 6 3 см.
Тогда, Ve (1) = 6
 3 см/с.
3 см/с.
Вектор скорости переносного движения точки Ve перпендикулярен линии
АМ1 и направлен в сторону вращения фигуры (см. рис. 3.7).
Относительное движение точки задано естественным способом, как закон изменения длины дуги ВМ. В этом случае скорость относительного движения
точки |
Vr = |
|
& |
|
= |
|
18πt |
|
. При t1 = 1 с |
Vr (1) = |
|
& |
|
= 18π = 56,5 см/с. Положи- |
|
|
|
|
|
|
|
||||||||||
|
Sr |
|
|
|
|
Sr (1) |
|
||||||||
тельное значение производной |
& |
|
|
|
|
что относительное движение |
|||||||||
Sr (1) указывает, |
|
||||||||||||||
точки в положении М1 происходит в положительном направлении, указанном на рис. 3.7 дуговой стрелкой Sr . Вектор Vr относительной скорости точки в положении М1 направлен по касательной к траектории относительного движения в сторону положительного направления движения (см. рис. 3.7).
Абсолютную скорость точки находим по теореме сложения скоростей
V =Ve + Vr . Направление вектора абсолютной скорости, полученное по правилу сложения векторов, показано на рис. 3.5. Для определения величины абсолют-
ной скорости выбираем прямоугольные оси координат М1xy (см. рис. 3.7) и про-
ецируем обе части векторного равенства теоремы сложения скоростей на эти
оси. Получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
=V cos60o = 3 |
|
|
= 5,2 см/с, |
||||||||||
x |
3 |
||||||||||||||
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
+ 56,5= 29,5 см/с. |
|||||||
Vy = −Vecos30o + Vr = - 6 |
|
× |
|
|
3 |
||||||||||
3 |
|||||||||||||||
|
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
= |
|
= 29,95 см/с. |
|||||||||
Модуль абсолютной скорости: V = |
|
Vx2 + Vy2 |
5,22 + 29,52 |
||||||||||||
Абсолютное ускорение точки определяем по теореме Кориолиса, кото-
рая при вращательном переносном движении имеет вид:
r |
r r |
r r |
r |
a |
= arτ + arn + aeτ + aen + aк . |
||
68
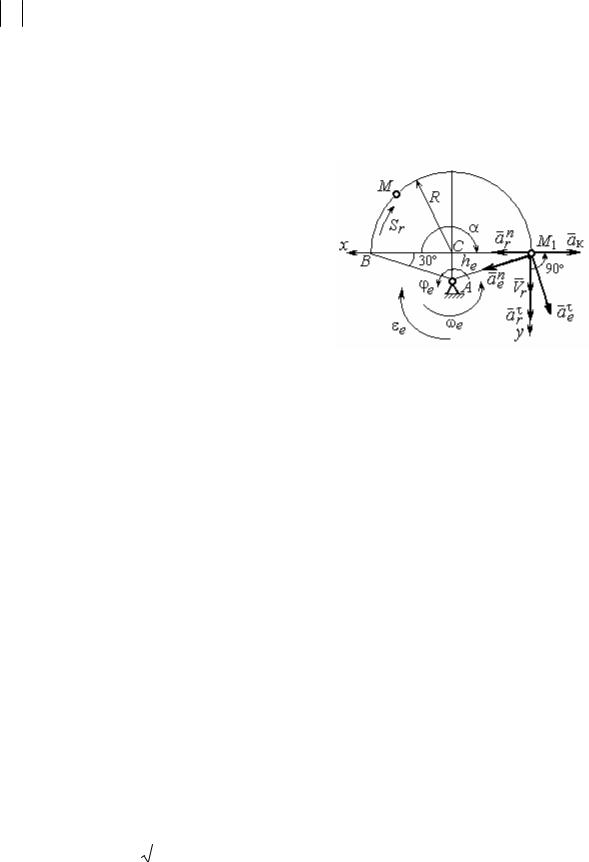
Относительное касательное ускорение arτ вычисляется по формуле: arτ = S&&r . По условию задачи вторая производная S&&r = 18π = 56,5 см/с2 – посто-
янная величина. Так как значение второй производной S&&r положительно, век-
rτ
тор ускорения ar направлен по касательной к траектории относительного дви-
жения в точке М1 в сторону положительного направления относительного дви-
жения, отмеченного дуговой стрелкой Sr . |
|
|
|
|
|||||||||||||||||||
|
Относительное нормальное ускоре- |
|
|
|
|
||||||||||||||||||
ние |
|
точки |
|
вычисляется |
по |
формуле |
|
|
|
|
|||||||||||||
V 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
an = |
r |
|
|
|
и |
в |
момент t |
= 1 |
с равно: |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
r |
R |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
arn (1) = |
V 2 |
(1) |
|
(18π)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
r |
|
= |
|
|
|
|
|
= 355,3 см/с2. Вектор |
Рис.3.8. Расчетная схема |
|
|||||||||||
|
|
R |
9 |
|
|
|
|||||||||||||||||
|
|
|
|
|
r |
направлен по радиусу диска к |
для определения абсолютного |
|
|||||||||||||||
|
|
|
|
|
ускорения точки |
|
|
|
|||||||||||||||
ускорения arn |
|
|
|
||||||||||||||||||||
центру С (см. рис. 3.8). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Переносное касательное ускорение вычисляется по формуле: aτ |
= ε |
h , |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
e e |
где угловое ускорение εe = |
|
ϕe |
|
. Вычислим производную ϕe = − 4 рад/с |
2 |
. Угло- |
|||||||||||||||||
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
&& |
|
|
|
|
&& |
|
|
|
|
вое ускорение εe = |
|
ϕe |
|
= 4 рад/с |
2 |
постоянно и не зависит от времени. |
|
|
|
||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
&& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отрицательное значение производной ϕe < 0 при условии, что расчетная |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
&& |
|
|
|
величина угловой скорости положительна: ϕ& e > 0, означает, что вращательное движение замедленное и переносное угловое ускорение εe направлено в сторо-
ну, противоположную направлению вращения.
rτ
Вектор ae переносного касательного ускорения точки в её положении М1
перпендикулярен линии АМ1 и направлен противоположно вектору перенос-
ной скорости Ve (см. рис. 3.8). Модуль переносного касательного ускорения ра-
вен: aτ = aτ = ε |
h = 24 |
|
= 41,6 см/с2. |
|
3 |
||||
e |
e |
e e |
||
69
