
MetodTM1
.pdf
Министерство образования и науки РФ ФГБОУ ВПО
«Уральский государственный горный университет»
Ю. М. Казаков
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
сборник заданий для расчетно-графических работ
Учебно-методическое пособие
для самостоятельной работы студентов
Екатеринбург
2015

Министерство образования и науки РФ ФГБОУ ВПО
«Уральский государственный горный университет»
ОДОБРЕНО
Методической комиссией горно-механического факультета
« » 2015 г.
Председатель комиссии проф. В. П. Барановский
Ю. М. Казаков
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
сборник заданий для расчетно-графических работ
Учебно-методическое пособие
для самостоятельной работы студентов
Издание УГГУ |
Екатеринбург, 2015 |
К 87
Рецензент: В. И. Саитов, д-р техн. наук, профессор, кафедра ГМК Уральского государственного горного университета
Учебно-методическое пособие рассмотрено на заседании кафедры технической механики __ ______ 2015 (протокол № ___) и рекомендовано для издания в УГГУ.
Казаков Ю. М.
К87 ТЕОРЕТИЧЕСКАЯ МЕХАНИКА. Сборник заданий для расчётно-графических работ. Учебно-методическое пособие для самостоятельной работы студентов / Ю. М. Казаков. – Екатеринбург: Изд-во УГГУ, 2015. – 156 с.
Учебно-методическое пособие содержит краткие методические указания, контрольные задания и примеры выполнения заданий по темам: «Статика твердого тела. Равновесие произвольной плоской и пространственной систем сил», «Кинематика вращательного движения твердого тела», «Кинематика плоскопараллельного движения твердого тела. Определение скоростей и ускорений точек твёрдого тела», «Сложное движение точки», «Динамика точки. Дифференциальные уравнения движения точки. Прямолинейные колебания. Применение теоремы об изменении кинетической энергии при исследовании движения точки», « Применение общих теорем динамики к исследованию движения механической системы», «Принципы механики. Применение общего уравнения динамики к исследованию движения механической системы», «Уравнения Лагранжа II рода».
© Казаков Ю. М., 2015 ©Уральский государственный горный университет, 2015
ОГЛАВЛЕНИЕ |
|
1. СТАТИКА ТВЕРДОГО ТЕЛА .............................................................................................. |
4 |
1.1. Основные виды связей и их реакции ...................................................................... |
4 |
1.2. Моменты силы относительно центра и относительно оси. Пара сил. |
|
Момент пары..................................................................................................................... |
5 |
1.3. Условия равновесия систем сил................................................................................ |
7 |
1.4. Задание С1. Равновесие произвольной плоской системы сил. |
|
Равновесие системы тел ................................................................................................... |
8 |
1.5. Задание С2. Равновесие пространственной системы сил ...................................... |
17 |
2. КИНЕМАТИКА ТОЧКИ И ТВЕРДОГО ТЕЛА.................................................................. |
26 |
2.1. Кинематика точки. Основные параметры движения точки................................... |
26 |
2.2. Вращение тела вокруг неподвижной оси ............................................................... |
28 |
2.3. Плоскопараллельное движение твёрдого тела....................................................... |
29 |
2.4. Задание К1. Определение скоростей и ускорений точек твердого тела |
|
при поступательном и вращательном движениях......................................................... |
32 |
2.5. Задание К2. Определение скоростей точек твёрдого тела |
|
при плоскопараллельном движении.............................................................................. |
38 |
2.6. Задание К3. Определение ускорений точек твёрдого тела |
|
при плоскопараллельном движении.............................................................................. |
46 |
3. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ ...................................................................................... |
57 |
3.1. Основные понятия сложного движения точки ...................................................... |
57 |
3.2. Задание К4. Определение скорости и ускорения точки при сложном движении60 |
|
3

1. СТАТИКА ТВЕРДОГО ТЕЛА
Статика представляет раздел теоретической механики, в котором рас-
сматриваются свойства сил, приложенных к твердому телу, изучается приведе-
ние сложных систем сил к более простому виду и определяются условия равно-
весия твердых тел.
1.1. Основные виды связей и их реакции
Опора тела на гладкую плоскость (поверхность) без трения. Реакция приложена в точке касания и направлена перпендикулярно к общей касательной соприкасающихся поверхностей. В случае, когда одна из соприкасающихся гладких поверхностей является точкой, например, опора углом, или на угол
(рис. 1.1, а), реакция направлена по нормали к другой поверхности. Гибкая связь. Если на тело наложена связь в виде гибкой нерастяжимой нити (каната,
троса), то реакция связи (натяжение нити) T приложена к телу и направлена вдоль нити (рис. 1.1, b). Цилиндрический шарнир (подшипник) создает со-
единение, при котором одно тело может вращаться по отношению к другому.
Реакция цилиндрического шарнира лежит в плоскости, перпендикулярной оси шарнира. При решении задач реакцию цилиндрического шарнира RA изобра-
жают ее составляющими X A и YA , взятыми по направлениям координатных
осей (рис. 1.1, c). Величина реакции определяется по формуле: RA = 
 X A2 + YA2 .
X A2 + YA2 .
Реакция прямолинейного невесомого стержня с шарнирными соединения-
ми на краях направлена вдоль самого стержня, а криволинейного – вдоль ли-
нии, соединяющей точки крепления стержня (рис. 1.1, d). Реакция подвижной опоры RB (рис. 1.1, e) направлена по нормали к поверхности, на которую опи-
раются катки опоры. Жесткая заделка препятствует не только линейным пере-
мещениям тела, но и повороту. Реакция заделки состоит из силы реакции RA и
4
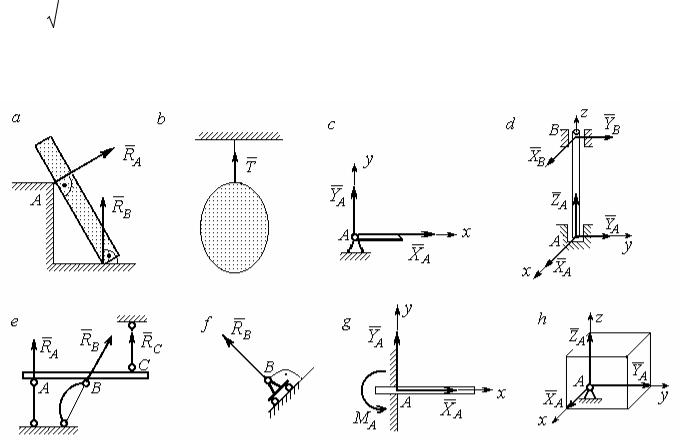
пары сил с моментом M A (рис. 1.1, f). При решении задач силу реакции жест-
кой заделки RA изображают ее составляющими X A и YA , взятыми по направ-
лениям |
координатных осей. Модуль реакции определяется по формуле |
||
|
|
|
. Виды связей и их реакции показаны на рис. 1.1. |
RA = |
X A2 + YA2 |
||
Рис. 1.1. Виды связей и их реакции:
а – реакция опоры тела на гладкую поверхность без трения; b – реакция связи гибкой нерастяжимой нити; с – реакция цилиндрического шарнира; d – реакция подшипника и подпятника; е – реакция невесомого стержня; f – реакция подвижной опоры; g – реакция жесткой заделки;
h – реакция пространственного шарнира
1.2. Моменты силы относительно центра и относительно оси. Пара сил. Момент пары
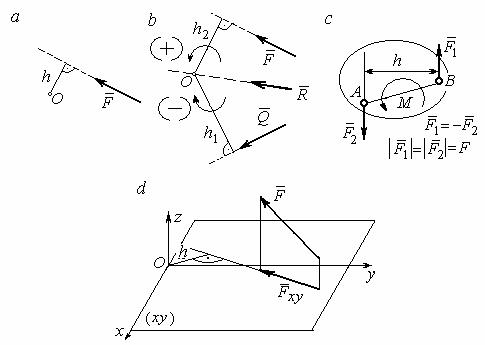
Алгебраическим моментом силы F относительно центра О M O (F) , или просто моментом силы F относительно центра О, называют взятое с соответ-
ствующим знаком произведение модуля силы F на кратчайшее расстояние h от центра О до линии действия силы: MO (F) = ±Fh (рис. 1.2, а). Величину h на-
зывают плечом силы. Момент силы относительно центра считается положи-
5
тельным, если сила стремится повернуть тело вокруг центра против хода часо-
вой стрелки и отрицательным – в обратном случае.
Рис. 1.2. Схемы для вычисления моментов сил:
а, b – момент силы относительно центра; с – момент пары сил; d – момент силы относительно оси
На рис. 1.2, b показано, что момент силы F относительно центра О поло-
жительный, а момент силы Q относительно того же центра – отрицательный.
Момент силы R относительно центра О равен нулю, так как линия действия этой силы проходит через центр О и плечо силы равно нулю.
Парой сил, или просто парой, (рис.1.2, с) называют систему двух равных по модулю сил, параллельных, направленных в противоположные стороны и не лежащих на одной прямой. Алгебраическим моментом пары сил, или момен-
том пары, называют взятое со знаком плюс или минус произведение модуля одной из сил пары на плечо пары – кратчайшее расстояние между линиями дей-
ствия ее сил. Правило знаков такое же, как и для момента силы. На рисунках пару часто изображают дуговой стрелкой, показывающей направление поворота твердого тела под действием пары (см. М на рис. 1.2, с).
6
Моментом силы относительно оси называют момент проекции этой си-
лы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью. На рис 1.2, d показано вычисление момента силы F относи-
тельно оси z: M z (F) = Fxy h, где Fxy – проекция силы F на плоскость xy, пер-
пендикулярную оси z, h – плечо проекции Fxy относительно центра О – точки пересечения оси z и плоскости xОy.
1.3. Условия равновесия систем сил
Плоской системой сил называется система сил, расположенных в одной плоскости.
Основная форма условий равновесия плоской системы сил. Для рав-
новесия плоской системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух осей прямо-
угольной системы координат, расположенной в плоскости действия сил, были равны нулю и сумма моментов сил относительно любого центра, находящегося в плоскости действия сил, также была равна нулю
å Fkx = 0, å Fky = 0, å M A (Fk ) = 0,
где Fkx , Fky – проекции всех сил на координатные оси; M A (Fk ) – моменты всех сил относительно произвольно выбранного центра А.
Пространственной системой сил называется система сил, расположен-
ных произвольно в пространстве.
Для равновесия пространственной системы сил необходимо и доста-
точно, чтобы суммы проекций всех сил на оси прямоугольной системы коорди-
нат были равны нулю и суммы моментов всех сил относительно тех же осей также были равны нулю:
å Fkx = 0, åFky = 0, å Fkz = 0,
7
åM x (Fk ) = 0, åM y (Fk ) = 0, åM z (Fk ) = 0,
где Fkx , Fky , Fkz – проекции всех сил на координатные оси x, y, z; M x (Fk ) ,
M y (Fk ) , M z (Fk ) – моменты всех сил относительно выбранных осей.
Равновесие систем тел
Связи, соединяющие части конструкции, называются внутренними в от-
личие от внешних связей, скрепляющих конструкцию с внешними телами, не входящими в данную конструкцию. Одним из способов решения задач на рав-
новесие сил, действующих на сочленённую конструкцию, является разбиение конструкции на отдельные тела и составление уравнений равновесия для ка-
ждого из тел, входящих в конструкцию. При этом в уравнения равновесия должны входить только силы, непосредственно приложенные к тому телу, рав-
новесие которого рассматривается.
1.4. Задание С1. Равновесие произвольной плоской системы сил. Равновесие системы тел
Каждый вариант задания включает 2 задачи по темам: «Равновесие про-
извольной плоской системы сил» и «Равновесие системы тел». В задачах требу-
ется определить реакции связей конструкции, исходя из условия равновесия произвольной плоской системы сил. Весом стержневых подпорок, поддержи-
вающих балочные конструкции, и блоков, через которые перекинуты невесомые нити, пренебречь.
Варианты заданий даны на рис. 1.3 – 1.6. Исходные данные приведены в табл. 1.1. Из таблицы исходных данных выбираются значения тех параметров,
которые указаны на схемах.
8
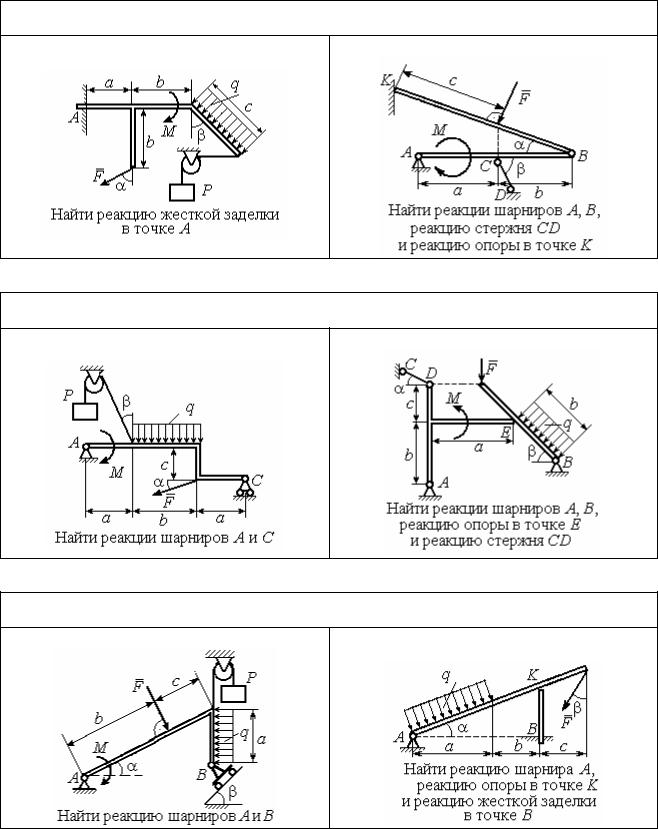
|
Варианты № 1, 11, 21 |
Задача 1 |
Задача 2 |
|
Варианты № 2, 12, 22 |
Задача 1 |
Задача 2 |
|
Варианты № 3, 13, 23 |
Задача 1 |
Задача 2 |
Рис. 1.3. Задание С1. Равновесие произвольной плоской системы сил. Равновесие системы тел. Номера вариантов задания 1 – 3, 11 – 13, 21 – 23
9
