Параграф 2. Дискретная многомерная случайная величина

Распределение двумерной дискретной случайной величины:

Свойства закона распределения двумерной дискретной случайной величины:

Свойство 1. Сумма вероятностей всех возможных значений, которые может принять дискретная многомерная случайная величина, равна единице:

Доказательство.

События 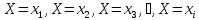и, состоящие в том, что в результате испытания случайная величинапримет соответственно значенияи, являются несовместимыми и единственно возможными, так как в таблице перечислены все возможные значения случайной величины, а значит, образуют полную группу. Следовательно, сумма их вероятностей равна единице.

Свойство доказано.

Свойство 2. Чтобы по таблице распределения найти вероятность того, что одномерная величина илипринимает определенное значение, надо просуммировать вероятности из соответствующей этому значению строки или столбца данной таблицы:

Доказательство.

Распределение одномерной дискретной случайной величины можно получить, вычислив вероятность событиякак сумму вероятностей несовместимых событий:

Свойство доказано.

Свойство 3. Условные распределения дискретных случайных величин и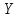равны:

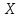Доказательство. Зафиксируем значение , то полученное распределение случайной величиныназывается условным распределениемпри условии. Вероятностиэтого распределения будут условными вероятностями события, при условии, что событиеуже произошло. Из определения условной вероятности:

Зафиксируем значение , то полученное распределение случайной величиныназывается условным распределениемпри условии. Вероятностиэтого распределения будут условными вероятностями события, при условии, что событиеуже произошло. Из определения условной вероятности:

Свойство доказано.

Пример 1.

Параграф 3. Функция распределения многомерной случайной величины

Функцией распределения многомерной случайной величины называется функция, выражающая вероятность совместного выполнения всех неравенств этих случайных величин:

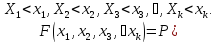
Глава 6. Закон больших чисел и предельные теоремы

Параграф 1. Неравенство Маркова

Теорема 1. Если случайная величин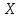а принимает только неотрицательные значения и имеет математическое ожидание, то для любого положительного числа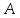верно неравенство:

Доказательство.

Теорема доказана.

Пример 1.

Параграф 2. Неравенство Чебышева

Теорема 1. Для любой величины, имеющей математическое ожидание и дисперсию, справедливо неравенство:

Доказательство.

Теорема доказана.

Пример 1.

Параграф 3. Теорема Чебышева

Параграф 4. Теорема Бернулли

Параграф 5. Центральная предельная теорема