
- •Раздел 1. Теория вероятности
- •Глава 1. Основные понятия и теоремы теории вероятностей Параграф 1. Понятие о случайном событии
- •Параграф 2. Действия над событиями
- •Параграф 3. Классическое определение вероятности
- •Параграф 4. Статистическое определение вероятности
- •Параграф 5. Геометрическое определение вероятности
- •Параграф 6. Элементы комбинаторики
- •Параграф 7. Теоремы произведения вероятностей
- •Параграф 8. Теоремы сложения вероятностей
- •Параграф 9. Формула полной вероятности
- •Параграф 10. Формула Байеса
- •Глава 2. Повторные независимые испытания Параграф 1. Формула Бернулли
- •Параграф 2. Формула Пуассона
- •Параграф 3. Локальная теорема Муавра-Лапласа
- •Параграф 4. Интегральная торема Муавра-Лапласа
- •Глава 3. Случайные величины Параграф 1. Понятие случайной величины
- •Параграф 2. Действия над случайными величинами
- •Параграф 3. Дискретная случайная величина
- •Параграф 4. Функция распределения
- •Параграф 5. Непрерывная случайная величина
- •Параграф 6. Мода и медиана. Квантили. Моменты случайных величин. Асимметрия и эксцесс
- •Глава 4. Основные законы распределения Параграф 1. Биномиальный закон распределения
- •Параграф 2. Закон распределения Пуассона
- •Параграф 3. Геометрическое распределение
- •Параграф 4. Гипергеометрическое распределение
- •Параграф 2. Дискретная многомерная случайная величина
- •Параграф 3. Функция распределения многомерной случайной величины
Параграф 4. Функция распределения
Функцией
распределения
случайной величины
 называется функция, выражающая для
каждого возможного значения вероятность
того, что случайная величина
называется функция, выражающая для
каждого возможного значения вероятность
того, что случайная величина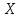 примет значение, меньшее его возможного
значения:
примет значение, меньшее его возможного
значения:

Свойства функции распределения:
Свойство 1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей:
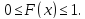
Доказательство.
Так как функция распределения выражает вероятность, то по 4 свойству вероятности:

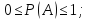

Свойство доказано.
Свойство 2.Функция распределения случайной величины есть неубывающая функция на всей числовой оси.
Доказательство.
Пусть
 и
и точки числовой оси, причем
точки числовой оси, причем .
Рассмотрим два несовместимых события
.
Рассмотрим два несовместимых события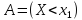 и
и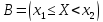 .
Тогда
.
Тогда
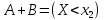 .
.
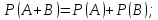
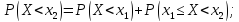

Так
как вероятность
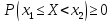 ,
то
,
то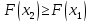 ,
т.е.
,
т.е. неубывающая функция.
неубывающая функция.
Свойство доказано.
Свойство доказано.
Свойство 3. Вероятность попадания случайной величины в интервал, сегмент и полуинтервал с одними и теми же концами одинаковы и равны приращению их функции на этом интервале:
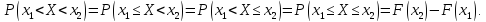
Доказательство.
Используя формулу из 2 свойства функции распределения:

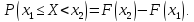
Доказательство.
Свойство доказано.
Свойство
4.
Если возможные значения случайной
величины принадлежат интервалу от
 до
до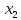 ,
то:
,
то:

Доказательство.
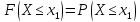 Событие
Событие
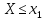 невозможно, следовательно, по 2 свойству
вероятности его вероятность равна нулю.
Событие
невозможно, следовательно, по 2 свойству
вероятности его вероятность равна нулю.
Событие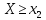 достоверно, следовательно, по 1 свойству
вероятности, его вероятность равна
единице.
достоверно, следовательно, по 1 свойству
вероятности, его вероятность равна
единице.
Свойство доказано.
Параграф 5. Непрерывная случайная величина
Дифференциальной
функцией распределения или
плотностью вероятности
непрерывной случайной величины
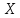 называется производная ее функции
распределения:
называется производная ее функции
распределения:
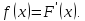
График плотности вероятности называется кривой распределения.
Свойства плотности вероятности непрерывной случайной величины:
Свойство 1. Плотность вероятности неотрицательная функция:
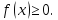
Доказательство.
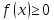 как
производная монотонно неубывающей
функции
как
производная монотонно неубывающей
функции
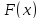 .
.
Свойство доказано.
Свойство
2.
Вероятность попадания непрерывной
случайной величины в интервал от
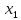 до
до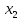 включительно равна определенному
интегралу от ее плотности в пределах
от
включительно равна определенному
интегралу от ее плотности в пределах
от до
до :
:

Доказательство.
Согласно свойству 3 функции распределения:

Так
как
 есть первообразная для плотности
вероятности
есть первообразная для плотности
вероятности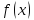 ,
то по формуле Ньютона-Лейбница приращение
первообразной на отрезке от
,
то по формуле Ньютона-Лейбница приращение
первообразной на отрезке от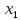 до
до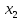 включительно есть определенный интеграл
включительно есть определенный интеграл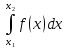 .
.
Свойство доказано.
Свойство 3. Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле:

Доказательство.
Свойство доказано.
Свойство 4. Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице:

Доказательство.
Свойство доказано.
Математическим
ожиданием
или средним
значением
 непрерывной случайной величины
непрерывной случайной величины называется величина несобственного
интеграла:
называется величина несобственного
интеграла:
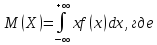
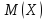 –математическое
ожидание непрерывной случайной величины
–математическое
ожидание непрерывной случайной величины
 ;
;
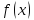 –плотность
непрерывной случайной величины
–плотность
непрерывной случайной величины
 ;
;
 –возможное
значение дискретной случайной величины
–возможное
значение дискретной случайной величины
 .
.
Дисперсией
или разбросом
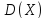 непрерывной случайной величины
непрерывной случайной величины называется величина несобственного
интеграла:
называется величина несобственного
интеграла:
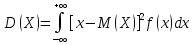
Все свойства математического ожидания и дисперсии дискретной случайной величины, справедливы и для непрерывных случайных величин.
Пример 1.
