
физика.методичка
.pdfТак как
ν = m/µ,
где µ – молярная масса, то
|
|
|
|
|
|
|
|
|
N = (m / µ)N A . |
|
|
|
|
У |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
Выразив в этой формуле массу как произведение плотности на |
||||||||||||||||||
|
объем V, получим |
|
|
|
|
|
|
|
|
|
|
|
|
Т |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
N = ρVN |
|
/ µ. |
|
|
|
|
(1.27) |
||||
|
|
Произведем |
вычисления, |
|
учитывая, что |
для |
|
воды |
µ = |
|||||||||||
|
= 18 10−3 кг/моль: |
|
|
|
|
|
|
|
|
Б |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
Н |
|
|||||||||
|
|
|
|
|
|
|
|
ρ =1 103 кг/м3; |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
||||
|
|
|
|
|
|
|
N A = 6,02 |
1023 |
моль−1; |
|
|
|
|
|||||||
|
|
|
|
103 10−9 |
|
|
р |
й |
|
|
|
|
||||||||
|
|
N = |
18 10−3 |
6,02 1023 |
|
молекул = 3,34 1019 |
молекул. |
|||||||||||||
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Массу m0 одной м лекулы м жно найти по формуле |
|
|
||||||||||||||||
|
|
|
|
|
и |
|
|
−3 |
= µ/ N A. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
m 0 |
|
|
|
|
(1.28) |
||||||
|
|
Подстав в в(1.28) значения µ и NA, найдем массу молекулы воды: |
||||||||||||||||||
|
|
о |
m |
|
= |
18 10 |
|
|
|
кг = 2,99 10−26 |
кг. |
|
|
|
||||||
|
п |
|
|
0 |
|
|
|
|
|
|
|
|
||||||||
е |
|
з |
|
|
6,02 1023 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||
|
|
Если молекулы воды плотно прилегают друг к другу, то можно |
||||||||||||||||||
Р |
считать, что на каждую молекулу приходится объем (кубическая |
|||||||||||||||||||
яч йка)
V = d 3,
41

где d – диаметр молекулы.
Отсюда |
|
d = 3 V . |
(1.29) |
0 |
|
|
Объем V0 найдем, разделив молярный объем Vm на число моле- |
У |
||||||||||||||||||||
кул в моле, т. е. на NA: |
|
|
|
|
|
|
|
|
|
|
Т |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
V0 =Vm / N A. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.30) |
|
|||||||
|
Подставим выражение (1.30) в (1.29): |
|
|
|
Н |
|
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
d = |
3 V |
m |
/ N |
A |
, |
|
|
|
|
|
|
где Vm = µ / ρ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|||||
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
d = 3 µ/(ρN A ). |
|
|
|
(1.31) |
|
|||||||
|
Проверим, дает ли правая часть вы ажен я (1.31) единицу длины: |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
µ |
|
|
|
|
т |
р |
|
|
|
|
|
||||||
|
|
|
|
[ |
|
] |
|
|
|
|
|
|
|
1 |
кг/моль |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
=1 м. |
|
|
|
|
|
[ρ |
|
и |
1 кг/м3 1 моль−1 |
|
|
|
|
|||||||||||||
|
|
][N |
A |
] |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Произведем выч слен я: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
п |
з3 |
18 10−3 |
|
|
|
|
|
|
−10 |
|
|
|
|||||||||
|
d |
= |
|
103 6,02 1023 |
м = 3,11 10 |
|
м. |
|
|
|||||||||||||
е |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
Задача |
1.12 |
|
|
|
|
|
|||||||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В баллоне объемом 10 л находится гелий под давлением 1 МПа и при температуре 300 К. После того как из баллона было взято 10 г
42
гелия, температура в нем понизилось до 290 К. Определить давление гелия, оставшегося в баллоне.
|
|
|
Дано: |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
V = 10 л = 1 10-2 м3; |
|
|
|
|
|
|
|
|
|
|
||||
|
|
P1 = 1 МПа = 1 106 Па; |
|
|
|
|
|
|
|
|
У |
|||||
|
|
T1 = 300 K; |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
T2 = 290 K; |
|
|
|
|
|
|
|
|
|
|
|
Т |
||
|
|
m = 10 г = 0,01 кг. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
P2 = ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
||
|
|
|
Для решения задачи воспользуемся уравнением Менделеева – |
|||||||||||||
|
|
Клапейрона, применив его к конечному состоянию газа: |
|
|||||||||||||
|
|
|
|
|
|
|
P2V = |
(m2 / µ)RT2 |
, |
|
Н |
(1.32) |
||||
|
|
|
|
|
|
|
Б |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
где m2 – масса гелия в баллоне в конечном состоянии; |
|
|
||||||||||||
|
|
|
µ – молярная масса гелия; |
|
|
|
|
|
|
|
||||||
|
|
|
R – универсальная газовая постояннаяй. |
|
|
|
||||||||||
|
|
|
Из уравнения (1.32) вы азим |
скомое давление: |
|
|
|
|||||||||
|
|
|
|
|
|
|
P2 |
|
и |
|
|
|
|
|
||
|
|
|
|
|
|
|
= m2RT2 |
/ (µV ). |
|
|
|
(1.33) |
||||
|
|
|
Массу m2 |
|
|
|
р |
|
|
|
|
|
|
|||
|
|
|
|
выразим через массу m1, соответствующую на- |
||||||||||||
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
||
|
|
чальному состоян ю, массу m гелия, взятого из баллона: |
|
|||||||||||||
|
|
|
|
|
|
т |
|
m2 |
= m1 − m. |
|
|
|
|
(1.34) |
||
|
|
|
|
гелия |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Массу m1 |
гелия найдем также из уравнения Менделеева – Кла- |
||||||||||||
|
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
ейр на, применив его к начальному состоянию: |
|
|
|
|||||||||||
|
|
|
о |
|
|
|
m = µPV / (RT ). |
|
|
|
|
(1.35) |
||||
|
п |
|
|
|
|
1 |
|
1 |
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Подставив выражение массы m1 в (1.34), а затем выражение m2 в |
|||||||||||||
|
|
(1.33), найдем |
|
|
|
|
|
|
|
|
|
|
|
|||
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
43 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
µP1V |
|
RT2 |
|
|
|
|
|
||
P2 |
= |
RT |
− m |
|
, |
Vµ |
|||||
|
|
1 |
|
|
|
или после преобразования и сокращения
|
|
|
|
|
|
|
|
|
|
|
P = |
T2 |
P − |
m |
|
|
RT2 |
. |
|
(1.36) |
У |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
T |
|
1 |
µ |
|
|
|
|
V |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
||
|
|
Произведем вычисления, учитывая, что |
|
|
|||||||||||||||||||||||||||
|
|
|
Н |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
R = 8,31 |
Дж моль K |
; |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
m = 4 10−3 кг моль; |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
290 |
|
|
|
|
10−2 |
|
8,31 |
|
|
|
|
|
й |
|
|
||||||||||
|
|
P = |
|
|
10−6 − |
|
|
|
|
|
|
|
|
|
|
|
|
290 |
Па = 3,64 105 |
Па. |
|
||||||||||
|
|
2 |
|
|
300 |
|
|
|
|
4 10−3 |
|
|
|
и |
Б |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
10−2 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача |
1.13 |
|
|
|
|
|
|
||||||||||
|
|
Вычислить |
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
удельные тепл емк сти п и постоянном объеме cV и |
|
||||||||||||||||||||||||||||
|
постоянном давлении |
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
cP |
не на и в дорода, принимая эти газы за |
|
|||||||||||||||||||||||||||
|
идеальные. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Дано: |
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Газы: |
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
неон (Ne); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
водор д (H2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
cV (Ne ) = ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
cP(N |
e |
) |
= ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cV (H |
2 |
) |
= ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cP(H2 ) = ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
44 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение
Удельные теплоемкости идеальных газов выражаются формулами |
||||||||||||||||||
|
|
|
|
|
|
c = i + 2 |
R |
; |
c |
= |
iR , |
|
|
У |
||||
|
|
|
|
|
|
|
|
|
(1.37) |
|||||||||
|
|
|
|
|
|
P |
|
|
2 µ |
|
V |
|
2µ |
|
Т |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
||||
где i – число степеней свободы молекулы газа; |
|
|||||||||||||||||
µ – молярная масса. |
|
|
|
|
|
|
|
|
|
|
||||||||
Для неона (одноатомный газ) i |
= 3; |
µ = 20 10-3 |
кг/моль. При |
|||||||||||||||
вычислениях по формулам (1.37) получим |
|
|
|
|
||||||||||||||
|
|
|
|
|
3 |
8,31 |
|
|
|
|
|
й |
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
cV |
= |
|
|
|
|
|
|
|
Дж/(кг К) = 6,24 10БДж/(кг К); |
|
|||||||
|
|
2 20 10−3 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
cP = (3 + 2) 8,31 |
Дж/(кг К) =1,04 103 Дж/(кг К). |
|
|||||||||||||||
|
|
|
|
|
|
|
о |
и |
|
|
|
|
||||||
|
|
|
|
2 20 10− |
3 |
|
|
|
|
|
|
|||||||
Для водорода (двуха |
|
|
мныйргаз) i = 5; µ = 2 10-3 |
кг/моль. При |
||||||||||||||
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|||
вычислениях по |
ем же ф рмулам получим |
|
|
|
||||||||||||||
|
c |
= |
|
5 |
т8,31 |
|
|
|
|
104 Дж/(кг К); |
|
|||||||
|
|
2 10−3 |
Дж/(кг К) =1,04 |
|
||||||||||||||
|
V |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
п |
з(5 + |
2) 8,31 |
Дж/(кг К) =1,46 104 Дж/(кг К). |
|
||||||||||||||
|
cP |
= |
2 |
2 10−3 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Р |
|
|
|
|
|
|
|
|
|
Задача 1.14 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и cP смеси неона и во- |
||||
еВычислить удельные теплоемкости cV |
||||||||||||||||||
дорода, если массовая доля неона w1 = 80%; массовая доля водорода
45

w2 = 20%. Значения удельных теплоемкостей газов взять из предыдущего примера.
Дано:
|
c |
|
= c |
|
|
|
) |
= 6,24 102 |
Дж/кг К; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
V |
V (N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cP |
= cP(N ) =1,04 103 Дж/кг К; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|||||||||||||||
|
|
1 |
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
c |
|
= c |
|
(H |
|
|
) |
=1,04 104 |
Дж/кг К; |
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
||||||||
|
V |
V |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
cP |
= cP(H |
2 |
) =1,46 104 |
Дж/кг К; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
w1 = 80 |
%; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
w2 |
= 20 |
%. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
||||||||
|
cP = ?; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|||
|
cV |
= ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
й |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Удельную теплоемкость смеси при постоянном объеме сV най- |
|
|||||||||||||||||||||||||||||
|
дем следующим образом. |
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Теплоту, необходимую для наг еван я смеси на ∆Т, выразим |
|
|||||||||||||||||||||||||||||
|
двумя способами: |
т |
|
|
|
|
и |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Q = cV (m1 + m2 )∆T; |
|
|
|
(1.38) |
|
|||||||||||||||||
|
|
|
V2 |
|
|
|
|
|
и |
|
|
m |
+ c |
|
m |
|
|
)∆T, |
|
|
|
(1.39) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
Q = (c |
|
|
2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
оV 1 |
|
V |
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
cV |
– удельная теплоемкость неона; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
1 |
го c (m + m ) = c m + c m , |
|
|
|
|||||||||||||||||||||||||
|
|
|
c |
|
|
|
||||||||||||||||||||||||||
|
|
|
– удельная теплоемкость водорода. |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Приравнявзправые части (1.38) и (1.39) и разделив обе части по- |
|
|||||||||||||||||||||||||||||
|
лученн |
|
равенства на ∆Т, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
V |
1 |
|
|
|
2 |
|
|
V |
|
|
1 |
|
|
V |
2 |
2 |
|
|
|
|
|||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
е |
|
|
|
|
|
c |
= c |
|
|
|
m1 |
|
+ c |
|
|
|
|
m2 |
|
|
|
(1.40) |
|
|||||||||
|
|
|
|
|
|
|
|
+ m |
|
|
|
m + m |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
V |
V1 m |
2 |
|
|
|
V2 |
|
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
46 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
cV |
= cV |
w1 |
+ cV |
|
w2 , |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
(1.41) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
где w1 = |
|
m1 |
|
|
; |
w2 = |
|
m2 |
|
– массовые доли неона и водоро- |
||||||||||||
|
|
m1 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
+ m2 |
|
|
m1 + m2 |
|
|
|
|
|
|
|
|||||||
|
|
да в смеси. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|||||
|
|
|
Подставив в формулу (1.41) числовые значения величин, найдем |
|||||||||||||||||||||
|
|
cV = (6,24 102 0,8 +1,04 104 0,2) |
Дж/(кг К) = 2,58 103 |
Т |
||||||||||||||||||||
|
|
Дж/(кг К). |
||||||||||||||||||||||
|
|
|
Рассуждая таким же образом, получим формулу для вычисления |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
удельной теплоемкости смеси при постоянном давлении |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
cP = cP1 w1 |
+ cP2 w2. |
|
Н(1.42) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
|||
|
|
|
Подставим в формулу (1.42) числовые значения величин: |
|||||||||||||||||||||
|
|
cP = (1,04 103 |
0,8 + 1,46 104 |
и |
|
|
Дж/(кг К). |
|||||||||||||||||
|
|
0,2) Дж/(кг К) = 3,75 103 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 1.15 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
||
|
|
|
В цилиндре под п ршнем находится водород массой 0,02 кг при |
|||||||||||||||||||||
|
|
температуре 300 К. В д р д сначала расширялся адиабатически, |
||||||||||||||||||||||
|
|
увеличив свой объем в 5 раз, а затем был сжат изотермически, при- |
||||||||||||||||||||||
|
|
|
|
|
|
|
: |
и |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
чем объем газа |
|
уменьшился в 5 раз. Найти температуру в конце |
||||||||||||||||||||
|
|
адиабатического расш рения и работу, совершенную газом при |
||||||||||||||||||||||
|
|
|
|
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
этих процессах. Иобразить процесс графически. |
|
|
||||||||||||||||||||
|
|
|
|
Дано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
m |
|
= 0,02 кг; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
е |
|
|
= 300 К; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Р |
|
n1 = 5; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
n2 |
= 5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
47 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
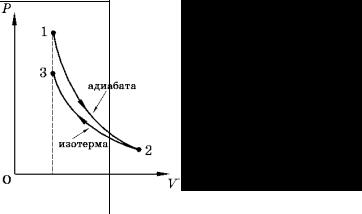
T2 =? А1 = ? А2 = ?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
Решение |
Рис. 1.5 |
Б |
Т |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Температуры и объемы газа, совершающего адиабатическийН |
|
|||||||||||||||||||||
процесс, связаны между собой соотношением |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
γ−1 |
и |
|
|
|
||||||||||
|
|
|
|
T2 |
V1 |
|
|
|
|
|
|
T2 |
|
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
= |
|
|
|
; |
|
|
|
|
= |
|
|
γ−1 |
, |
(1.43) |
|
||
|
|
|
|
T |
|
|
V |
|
|
р |
й |
|
|
||||||||||
|
|
|
1 |
|
2 |
|
|
|
|
|
1 |
|
|
|
n |
|
|
|
|
||||
где γ – отношение тепл емк сти газа п и постоянном давлении и |
|
||||||||||||||||||||||
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
постоянном объеме, для в д р да как двухатомного газа |
|
|
|||||||||||||||||||||
|
|
|
и |
|
|
|
|
V1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
γ |
|
= 1,4,оµ = 2 10-3 кг/моль; |
|
|
|
||||||||||||||
|
|
з |
|
|
|
|
|
|
V2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
о |
|
|
|
|
n |
|
= |
|
|
= 5. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда лучаем выражение для конечной температуры Т2: |
|
|||||||||||||||||||||
е |
|
|
|
|
|
|
|
|
|
|
|
T1 |
|
|
|
|
|
|
|
|
|
||
Р |
п |
|
|
|
|
|
T2 = |
|
. |
|
|
|
|
|
(1.44) |
|
|||||||
|
|
|
|
|
nγ−1 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
Подставляя числовые значения заданных величин, находим
48
|
|
|
|
|
|
|
|
|
|
T |
= |
300 |
|
= 300 К =157 К. |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
51,4−1 |
1,91 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Работа А1 газа при адиабатическом расширении может быть оп- |
|||||||||||||||||||||||||||||
|
ределена по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
||||||||||
|
|
|
|
|
|
|
|
A = m C |
(T −T ) |
= |
miR(T1 −T2 ) |
, |
|
Т |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(1.45) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
µ |
V |
|
1 |
|
2 |
|
|
2µ |
|
|
Н |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
где СV – молярная теплоемкость газа при постоянном |
объеме. |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|||||
|
Подставив числовые значения величин: R = 8,31 Дж/(моль К); i = 5 |
|||||||||||||||||||||||||||||
|
(для водорода как двухатомного газа); m = 0,02 кг; µ = 2 10−3 кг/моль; |
|||||||||||||||||||||||||||||
|
Т1 = 300 К; Т2 |
= 157 К в правую часть формулы (1.45) и выполняя |
||||||||||||||||||||||||||||
|
арифметические действия, получим |
й |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
0,02 5 8,31 |
|
|
|
|
и |
|
|
|
|
|
|
|
|
|||||||||||
|
|
A = |
|
|
|
|
|
(300 −157) |
Дж = 2,98 104 Дж. |
|
||||||||||||||||||||
|
|
1 |
|
|
|
2 10−3 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Работа А2 газа при |
|
|
|
м ческом процессе может быть выра- |
|||||||||||||||||||||||||
|
жена в виде |
|
|
|
|
|
|
|
|
изоте |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
т |
рV |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
V2 |
|
|
|
|
|
|
m |
|
|
1 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
A |
|
= |
µ |
|
RT ln |
3 |
; A |
= |
µ |
RT ln |
n |
|
, |
|
|
(1.46) |
||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
V |
2 |
|
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
и |
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||
|
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
где n2 = |
V3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
П дставим в формулу (1.46) числовые значения величин: |
|
||||||||||||||||||||||||||||
|
|
|
A = |
0.02 |
|
8,31 157 ln 1 |
Дж = −21 103 |
|
Дж. |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
2 |
|
|
|
2 10−3 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|||||
Р |
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
пЗнак «минус» показывает, что при сжатии газа работа соверша- |
||||||||||||||||||||||||||||||
|
тся над газом внешними силами. График процесса приведен на |
|||||||||||||||||||||||||||||
ерис. 1.5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 1.16
49
|
|
Тепловая машина работает по обратимому циклу Карно. Темпе- |
|
|||||||||||||
|
ратура нагревателя 500 К. Определить термический КПД цикла и |
|
||||||||||||||
|
температуру холодильника тепловой машины, если за счет каждого |
|
||||||||||||||
|
килоджоуля теплоты, полученной от нагревателя, машина соверша- |
|
||||||||||||||
|
ет работу 350 Дж. |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Дано: |
|
|
|
|
|
|
|
|
|
|
|
Т |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
A = 350 Дж; |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|||
|
T1 |
= 500 K. |
|
|
|
|
|
|
|
|
|
|
Н |
|||
|
T2 |
= ?; |
|
|
|
|
|
|
|
|
|
|
|
|||
|
η = ? |
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Термический КПД тепловой машины показывает, какая доля те- |
|
|||||||||||||
|
плоты, полученной от нагревателя, превращается в механическую |
|
||||||||||||||
|
работу. |
|
|
|
|
|
|
|
|
|
|
й |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
||
|
|
Термический КПД выражается формулой |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|||
|
|
|
|
|
|
|
|
η |
= А/Q1, |
|
|
(1.47) |
|
|||
|
|
|
|
|
|
ηот= = 0,35. |
|
|
|
|||||||
|
где Q1 – теплота, полученная |
наг евателя; |
|
|
|
|||||||||||
|
|
А – работа, совершенная раб чим телом тепловой машины. |
|
|||||||||||||
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
||
|
|
Подставив числовые значения в эту формулу, получим |
|
|
||||||||||||
|
|
|
|
|
и |
|
350 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
о |
|
1000 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Зная КПД ц кла, можно по формуле |
|
|
|
|
||||||||||
|
|
п |
з |
|
η = |
T1 −T2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|||
е |
|
|
|
|
|
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
о р д лить температуру холодильника Т2: |
|
|
|
||||||||||||
Р |
|
|
|
|
|
Т2 = Т1 (1 - η). |
|
|
(1.48) |
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
