
физика.методичка
.pdf
|
|
В рассматриваемом случае (ϕ = π/ 2) |
работа внешних сил опре- |
|||||||||||
|
деляется выражением |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
A = Iπr2 B . |
|
|
(3.33) |
||
|
|
Задачу можно решить и другим способом. Работа внешних сил |
||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
У |
|
по перемещению контура с током в магнитном поле равна |
|
||||||||||||
|
|
|
|
|
|
|
A = −I∆Ф = I(Ф1 −Ф2 ) , |
Т |
||||||
|
|
|
|
|
|
|
|
(3.34) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|
|
где Ф1 = BS = Bπr – магнитный поток, пронизывающий контур в |
|||||||||||||
|
начальный момент времени; |
|
|
|
|
|
|
|||||||
|
|
Ф2 = 0 – магнитный поток, пронизывающий контур после по- |
||||||||||||
|
ворота. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, |
|
|
|
|
|
й |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
A = Iπr2B, |
Б |
|
|
||
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
||
|
что совпадает с формулой (3.33). |
|
|
|
|
|||||||||
|
|
Произведем вычисления: |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
о |
|
|
|
|
|
||
|
|
|
|
A = 100 |
3,14 0,22 0,02 = 0,251 Дж. |
|
|
|||||||
|
|
|
|
|
антенна |
|
|
|
|
|
|
|||
|
|
|
|
и |
|
Задача 3.8 |
|
|
|
|||||
|
|
|
з |
|
|
|
|
(вертикальный проводник) |
длиной 2 м |
|||||
|
|
Автомоб льная |
|
|
|
|||||||||
|
движется с востока на запад в магнитном поле Земли со скоростью |
|||||||||||||
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
60 км/ч. Вычислить разность потенциалов между концами провод- |
|||||||||||||
|
ника. Г ри нтальную составляющую индукции магнитного поля |
|||||||||||||
|
п |
|
|
|
|
|
-5 |
Тл. |
|
|
|
|
|
|
|
Земли ринять равной 2 10 |
|
|
|
|
|
||||||||
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
111 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
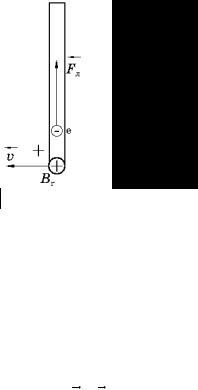
Дано:
l= 2 м;
υ= 60 км/ч;
Br = 2 10−5 Тл;
α= 90о.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U = ? |
|
|
|
|
|
|
|
|
|
|
Т |
||
|
|
|
|
|
|
|
|
|
|
Рис. 3.8 |
Н |
|
||
|
|
|
|
|
|
|
|
|
|
Б |
|
|
||
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
||
|
|
|
|
|
|
|
|
|
й |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Так как проводник разомкнут, тока в нем не будет, и разность |
|
|||||||||||
|
потенциалов U на концах проводника равна ЭДС индукции: |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
U = B l υ sin α, |
|
|
|
|
||
|
где l – длина проводника; |
|
|
р |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||
|
|
υ – скорость его движения; |
|
|
|
|
|
|||||||
|
|
α – угол между векторами B и υ. |
|
|
|
|
||||||||
|
|
Смещение электронов в вер икальной антенне автомобиля под |
|
|||||||||||
|
|
|
и |
|
|
|
|
|
|
|||||
|
действием силы Лоренца |
|
Fопроисходит за счет горизонтальной со- |
|
||||||||||
|
|
|
з |
|
|
|
л |
|
|
|
|
|
||
|
|
|
тнмагн ого поля Земли, т.е. |
B = Bг; sin α =1 . |
|
|||||||||
|
ставляющей индукц |
|
|
|||||||||||
|
в рхнийжительно. |
|
|
магнитного поля Земли направлены с юга |
|
|||||||||
|
Так как силовые л н |
|
|
|
||||||||||
|
на север, то п д действием Fл электроны переместятся к верхнему |
|
||||||||||||
|
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
концу антенны. Таким образом, нижний конец антенны зарядит- |
|
||||||||||||
|
ся ол |
и |
будет иметь более высокий потенциал, чем |
|
||||||||||
Р |
Возникшая разность потенциалов равна |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
е |
|
|
|
|
|
|
U = Bгlυ. |
|
|
|
|
|||
112 |
|
|
|
|
|
|
|
|
|
|
|
|
||

Произведем вычисления:
U = 2 10−5 2 60 1000 = 6,67 10−6 В. 3600
|
|
|
|
|
|
|
|
|
|
|
|
Задача 3.9 |
|
|
У |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
|
|
|
В однородном магнитном поле (В = 0,1 Тл) равномерно с часто- |
||||||||||||||
|
|
той 10 с-1 вращается рамка, содержащая 1000 витков, плотно приле- |
|||||||||||||||
|
|
гающих друг к другу. Площадь рамки – 150 cм2. Ее вращение со- |
|||||||||||||||
|
|
вершается вокруг оси, лежащей в ее плоскости и перпендикулярной |
|||||||||||||||
|
|
линиям магнитной индукции. Найти максимальную ЭДС индукции |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
во вращающейся рамке. Определить количество электричества, ко- |
|||||||||||||||
|
|
торое протечет через рамку за время ее поворота на угол 30° в слу- |
|||||||||||||||
|
|
чаях, если угол поворота рамки изменяется: 1) от 0Ндо 30°; 2) от 30 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
й |
Ом (рис. 3.9). |
||
|
|
до 60°. Сопротивление рамки принять равным 10 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
Дано: |
|
|
|
|
|
р |
|
|
|
|
|||
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
||||
|
|
B = 0,1 Тл; |
|
|
|
т |
|
|
|
|
|
|
|||||
|
|
ν |
=10 с-1; |
|
и |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
N =1000; |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
з |
|
|
|
|
|
|
|
|
||||
|
|
S =150 |
см |
2 |
; |
|
|
|
|
|
|
|
|
||||
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
||||
|
|
ϕ |
0 |
= 0 ; |
|
|
|
|
|
|
|
|
|
|
|
||
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
ϕ |
1 |
= 30 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
ϕ |
2 |
= 60о. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε max = ? |
|
|
|
|
|
|
|
|
Рис. 3.9 |
|
|
|||||
еq = ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
113 |
|
|
|
|
|
Решение |
|
|
|
|
|
|
|||||
|
ЭДС электромагнитной индукции определяется уравнением |
|
||||||||||||||
|
|
|
|
|
ε = − |
dψ |
, |
|
|
|
|
(3.35) |
|
|||
|
|
|
|
|
|
|
|
|
|
У |
||||||
|
|
|
|
|
|
|
dt |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Т |
|||||
где ψ – потокосцепление, равное в данном случае ψ = ФN. |
||||||||||||||||
|
|
|||||||||||||||
|
При вращении рамки магнитный поток, пронизывающий рамку в |
|
||||||||||||||
момент времени t, определяется уравнением |
|
|
Н |
|
||||||||||||
|
|
|
|
|
Ф = B S cos (ωt + α), |
|
|
|||||||||
|
|
|
|
|
Б |
(3.36) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где α – угол, образуемый нормалью к поверхноcти рамки и направ- |
|
|||||||||||||||
лением силовых линий при t = 0; |
|
|
й |
|
|
|
||||||||||
|
ω = 2πν |
|
i |
|
|
|
|
|
|
|
|
|
||||
|
– циклическая (круговая) частота. |
|
|
|
|
|||||||||||
|
Из выражения (3.37) вытекает |
индукции |
принимает вид |
|
||||||||||||
|
С учетом (3.36) выражение для ЭДС |
|
|
|
||||||||||||
|
|
|
|
|
|
р |
ωt |
+ α) . |
|
|
|
|||||
|
|
|
ε = |
NBS 2πν sin( |
|
(3.37) |
|
|||||||||
|
|
|
|
т |
= NBS 2πν. |
|
|
|
|
|
||||||
|
|
|
|
|
εi max |
|
|
|
(3.38) |
|
||||||
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|||
|
Произведем выч слен яо: |
|
|
|
|
|
|
|
|
|||||||
|
ε i max =1000 0,1 1,5 10−2 |
2 3,14 10 = 94,2 |
B . |
|
|
|||||||||||
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Мгн веннзе значение индуктивного тока в рамке определяется |
|
||||||||||||||
закон м Ома |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Р |
п |
|
|
|
Ii = εi |
, |
|
|
|
|
|
|
|
|||
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где R – сопротивление.
114
|
|
|
|
I i = − |
|
|
1 |
|
|
dψ |
|
= − |
|
1 |
|
|
N |
dФ |
. |
|
|
(3.39) |
||||||||||||
|
|
|
|
|
R |
dt |
|
R |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
||||||||||||
|
|
Мгновенное значение тока |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
I i |
= dq |
, |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
Н |
|||||
|
поэтому (3.39) можно переписать в виде |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
dq = − |
1 |
N |
dФ |
; |
|
|
|
Т |
|||||||||||||||||||
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
(3.40) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
dq = −N |
|
dФ |
|
Б |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и1 |
|
|
|
|
|
|
||||||||||||||
|
|
После интегрирования выражен я (3.40) получим |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
Q |
|
р |
|
|
Ф2 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
∫dq = − |
|
|
|
N ∫dФ; |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
R |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ф1 |
|
|
|
|
|
|
|||||||
|
|
|
|
о |
|
Ф2 −Ф1 |
|
|
|
|
|
(3.41) |
||||||||||||||||||||||
|
|
|
з |
|
|
|
q |
= |
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Так как Фи= BScosϕ |
, окончательно имеем |
|
|
|
||||||||||||||||||||||||||||
|
п |
|
q = NBS (cosφ |
0 |
|
−cosφ ) . |
|
|
(3.42) |
|||||||||||||||||||||||||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
|
В первом случае |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
q |
|
= NBS |
(1 −cos 30о) . |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
115 |

Во втором случае
|
|
|
|
|
|
|
|
q 2 |
= NBS (cos30о |
−cos60о) . |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
У |
|
|
|
Произведем вычисления: |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
Т |
|||||||||
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|||
|
|
|
|
q |
=1000 0,1 1,5 10−2 |
(1 −0,866)= 2,06 10−2 |
Кл; |
|
|
|||||||||
|
|
|
1 |
|
|
|
|
10 |
|
|
|
|
|
|
Н |
|
||
|
|
|
|
q |
=1000 0,1 1,5 10−2 |
(0,866 |
−0,5)= 5,5 10−2 |
|
||||||||||
|
|
|
|
Кл. |
|
|
||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 3.10 |
й |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При некоторой величине тока плотность энергии магнитного по- |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
ля длинного соленоида без сердечника равна 0,2 ДжБ/м . Во сколько |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
при |
|
|
|
|
||
|
раз увеличится плотность энергии поля |
том же токе, если соле- |
|
|||||||||||||||
|
ноид будет иметь сердечник? При |
|
ен |
задачи воспользоваться |
|
|||||||||||||
|
графиком рис. 3.10. |
|
|
реш |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
Дано: |
|
|
|
|
о |
|
|
|
|
|
|
|
||
|
ω1 = 0,2 Дж. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
ω2 |
|
|
|
|
т |
|
|
|
|
|
|
|
||||
|
|
|
= ? |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
ω1 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
з |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
е |
|
|
|
|
|
|
|
|
Рис. 3.10 |
|
|
|
|
|||||
Р |
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Объемная плотность энергии магнитного поля определяется соотношением
116

|
|
|
|
|
|
|
ω1 = |
1 |
µµ 0 H 2 , |
|
|
|
(3.43) |
|||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
где µ – магнитная проницаемость вещества; |
|
|
|
|
|||||||||||||||
|
|
µ0 – магнитная постоянная; |
|
|
|
|
|
|
|
|
|
У |
||||||||
|
|
H – напряженность магнитного поля. |
|
|
|
|||||||||||||||
|
|
|
|
Т |
||||||||||||||||
|
|
Для соленоида величина Н равна |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
H = nI, |
|
|
Н |
(3.44) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
где n = N/l – число витков, приходящихся на единицу длины соле- |
|||||||||||||||||||
|
ноида; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I – ток. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как ток соленоида не меняется, величина Н в соответствии с |
||||||||||||||||||
|
|
|
|
|
|
|
ω |
|
|
|
µ й |
|
|
|
||||||
|
(3.44) будет неизменной в обоих случаях. Следовательно, отноше- |
|||||||||||||||||||
|
ние ω2 / ω1 |
|
равно |
|
|
|
и |
Б |
|
|
||||||||||
|
|
|
|
|
|
|
ω2 |
= |
µ |
2 |
|
. |
|
|
|
(3.45) |
||||
|
|
|
|
|
|
|
р |
1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
о |
1 |
|
|
|
|
|
|
|
|
|
||||
|
|
Величина µ может быть найдена по формуле |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
µ |
= |
|
B |
|
|
. |
|
|
|
|
|||
|
|
|
|
и |
|
µ0H |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Найдем |
наченте Н из формулы (3.43), записанной для случая, |
|||||||||||||||||
|
когда |
|
|
д не содержит сердечника ( µ1 =1): |
|
|
|
|||||||||||||
е |
солено |
|
|
H |
= |
|
|
2ω1 ; |
|
|
|
(3.46) |
||||||||
|
|
|
|
|
|
|
|
|
|
µ0 |
|
|
|
|
|
|||||
Р |
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
H = |
2 0,2 |
|
|
|
= 560 А/м. |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
4 3,14 10−7 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
117 |

|
|
В соответствии с графиком рис. 3.10, этому значению Н соответ- |
|
|||||||||||||||
|
ствует величина B2 |
= 1,15 Тл. Следовательно, величина µ2 равна |
|
|||||||||||||||
|
|
|
|
µ2 |
= |
|
|
1,15 |
|
=1,6 |
103 . |
|
|
|
||||
|
|
|
|
560 |
4 3,14 10−7 |
|
|
У |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
В соответствии с формулой (3.45), во столько же раз увеличива- |
||||||||||||||||
|
ется плотность энергии в соленоиде с сердечником: |
|
Т |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
ω2 =1,6 |
103 . |
|
|
Н |
|
|||
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача |
3.11 |
й |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Определить частоту собственных колебаний колебательного кон- |
|
|||||||||||||||
|
тура, который состоит из воздушного плоского конденсатораБ |
с пло- |
|
|||||||||||||||
|
щадью каждой из пластин 100 см2 |
и |
|
|
|
|
||||||||||||
|
расстоян ем между ними 3 мм и |
|
||||||||||||||||
|
катушки длиной 10 |
и радиусом 0,5 см. Ч сло в тков катушки – 500. |
|
|||||||||||||||
|
Активное сопротивление конту а п |
нять авным нулю. |
|
|
|
|||||||||||||
|
|
Дано: |
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
||
|
d = 3 мм; |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|||||
|
l = 10 см; |
|
|
и |
|
|
|
|
|
|
||||||||
|
S = 100 м2; |
|
|
|
|
т |
|
|
|
|
|
|
|
|
||||
|
r = 0,5 см; |
|
з |
|
|
|
|
|
|
|
|
|||||||
|
N = 500. |
|
|
|
|
|
|
|
|
|
||||||||
|
ν = ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
соб |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
п |
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|||
Пе |
|
|
ственных колебаний в контуре без активного сопро- |
|
||||||||||||||
|
|
риод |
|
|
||||||||||||||
|
тивл ния о ределяется формулой Томсона |
|
|
|
|
|||||||||||||
Р |
|
|
|
|
|
|
|
|
T = 2π |
LC , |
|
|
|
(3.47) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где L – индуктивность контура;
118

С – его электроемкость. Индуктивность соленоида
|
|
|
|
|
|
|
|
|
|
L = µ0 |
N 2 |
|
S = µ0 |
|
N 2 |
|
πr2 . |
|
|
|
|
(3.48) |
|||||||||||||
|
|
|
|
|
|
|
|
l |
|
|
l |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
||||||
|
|
Емкость конденсатора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C = |
ε0S |
. |
|
|
|
|
|
Н |
(3.49) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
С учетом формул (3.47) и (3.48) выражение для частотыТколеба- |
|||||||||||||||||||||||||||||||||
|
ний принимает вид |
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
ν = |
1 |
= |
1 |
|
|
|
= |
1 |
|
|
|
|
|
|
ld |
|
|
. |
|
(3.50) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
2π |
LC |
|
|
|
|
|
|
|
Б |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε0µ0πr SN |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Произведем вычисления: |
|
|
|
|
|
|
|
|
|
|
10−3 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
ν = |
|
1 |
|
|
|
|
|
|
о |
|
0,1 3 |
|
|
|
|
|
|
= |
|
||||||||||||||
|
|
2 |
3,14 |
|
8,85 10−12 4 |
3,14 10−7 3,14(0,5 10−2 )210−2 |
|
||||||||||||||||||||||||||||
|
|
|
|
500 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
и |
|
=1,867 106 c−1. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
рольная работа №3 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
о |
|
|
Кон |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Таблица вариантов |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
п |
|
|
|
|
|
|
|
Номера |
задач |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
№ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
0 |
|
310 |
|
|
320 |
|
330 |
|
|
|
340 |
|
|
|
350 |
|
|
360 |
|
370 |
|
380 |
|
||||||||||
е |
1 |
|
301 |
|
|
311 |
|
321 |
|
|
|
331 |
|
|
|
341 |
|
|
351 |
|
361 |
|
371 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Р |
|
2 |
|
302 |
|
|
312 |
|
322 |
|
|
|
332 |
|
|
|
342 |
|
|
352 |
|
362 |
|
372 |
|
||||||||||
|
3 |
|
303 |
|
|
313 |
|
323 |
|
|
|
333 |
|
|
|
343 |
|
|
353 |
|
363 |
|
373 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
4 |
|
304 |
|
|
314 |
|
324 |
|
|
|
334 |
|
|
|
344 |
|
|
354 |
|
364 |
|
374 |
|
||||||||||
|
|
5 |
|
305 |
|
|
315 |
|
325 |
|
|
|
335 |
|
|
|
345 |
|
|
355 |
|
365 |
|
375 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
119 |
|

6 |
306 |
316 |
326 |
336 |
346 |
356 |
366 |
376 |
7 |
307 |
317 |
327 |
337 |
347 |
357 |
367 |
377 |
8 |
308 |
318 |
328 |
338 |
348 |
358 |
368 |
378 |
9 |
309 |
319 |
329 |
339 |
349 |
359 |
369 |
379 |
|
301. По плоскому контуру, изобра- |
|
|
|
|
|
|
У |
||||||||||
женному на рис. 3.11, течет ток силой |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||||||
1,0 А. Угол |
между прямолинейными |
|
|
|
|
|
|
|
||||||||||
участками – прямой. Радиусы равны |
|
|
|
|
|
|
|
|||||||||||
10 см и 20 см. Найти магнитную ин- |
|
|
Н |
|
||||||||||||||
дукцию в точке С. |
|
|
|
|
|
|
|
|
|
Рис. 3.11 |
|
Т |
||||||
|
302. Ток, |
равный 1 А, |
циркулирует |
|
|
|
||||||||||||
|
|
|
Б |
|
||||||||||||||
в контуре, имеющем форму равнобоч- |
|
|
|
|
|
|
|
|||||||||||
ной трапеции (рис. 3.12). Отношение |
|
|
|
|
|
|
|
|||||||||||
оснований трапеции – 2. |
|
Найти маг- |
|
й |
|
|
|
|||||||||||
нитную индукцию магнитного поля |
в |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
||
точке А, лежащей в плоскости трапе- |
|
|
|
|
|
|
|
|||||||||||
ции. Меньшее основание |
трапец |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
||
равно 100 мм; расстояние b = 50 мм. |
|
|
|
|
Рис. 3.12 |
|
|
|
||||||||||
|
303. Ток 5 А течет по тонкому п о- |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
ного |
|
|
|
|
|
|
|
|
|
||
воднику, изогнутому, как п казано на |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
т |
|
|
- |
|
|
|
|
|
|
|
|||
рис. 3.13. Радиус изогнут й части п |
|
|
|
|
|
|
|
|
||||||||||
водника – 120 мм; угол ϕ |
= 90°. Найти |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
и |
|
|
поля |
|
|
|
|
|
|
|
||||
магнитную индукцию магни |
|
|
|
|
|
|
|
|
||||||||||
в точке 0. |
з |
|
|
|
|
|
|
|
|
|
Рис. 3.13 |
|
|
|
||||
|
304. Найти магн тную индукцию |
|
|
|
|
|
|
|
||||||||||
|
|
поля |
в точке О, если про- |
|
|
|
|
|
|
|
||||||||
магнитного |
|
|
|
|
|
|
|
|
||||||||||
водник с т к м 8 А имеет вид, пока- |
|
|
|
|
|
|
|
|||||||||||
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
занный на рис. 3.14. Радиус a = 20 см, |
|
|
|
|
|
|
|
|||||||||||
сторона b = 40 см. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
е |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.14 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
