
физика.методичка
.pdf
|
|
|
Во время экзаменационно-лабораторных сессий проводятся ла- |
|||||||||
|
|
бораторные работы. Цель лабораторного практикума – не только |
||||||||||
|
|
изучить те или иные физические явления, убедиться в правильности |
||||||||||
|
|
теоретических выводов, приобрести соответствующие навыки в об- |
||||||||||
|
|
ращении с физическими приборами, но и более глубоко овладеть |
||||||||||
|
|
теоретическим материалом. |
|
|
|
|
|
|||||
|
|
|
На экзаменах и зачетах, в первую очередь, выясняется усвоение ос- |
|||||||||
|
|
новных теоретических положений программы и умение творчески |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Т |
|
|
применять полученные знания к решению практических задач. Физи- |
||||||||||
|
|
ческая сущность явлений, законов, процессов должна излагаться четко |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|
|
и достаточно подробно. Только при выполнении этих условий знанияУ |
||||||||||
|
|
покурсу физики могутбытьпризнаныудовлетворительными. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
1. ФИЗИЧЕСКИЕ ОСНОВЫ КЛАССИЧЕСКОЙ МЕХА ИКИ. |
||||||||||
|
|
|
МОЛЕКУЛЯРНАЯ ФИЗИКА. |
ТЕРМОДИНАМИКА |
||||||||
|
|
|
|
|
|
|
|
иальной |
|
|
||
|
|
|
|
|
|
Примеры решения задач |
|
|||||
|
|
|
|
|
|
|
р |
3 |
|
|
||
|
|
|
|
|
|
|
Задача й1.1 |
|
||||
|
|
|
|
|
|
|
о |
3 |
точки вдоль оси имеет вид |
|||
|
|
|
Уравнение движения мате |
|
|
|||||||
|
|
|
|
точки |
X = A+Bt +Ct , |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
где А = 2 м; В = 1 м/с; С = –0,5 м/с . Найти координату, скорость и |
||||||||||
|
|
ускорение |
|
вмоментвремени 2 с. |
|
|
|
|||||
|
|
|
Дано |
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
X = A + зBt + C t ; |
|
|
|
|
|
|
|
|||
|
|
А = 2 м; |
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
||
|
|
В = 1 м/с; |
|
|
|
|
|
|
|
|
|
|
Р |
|
С = 0,5 м/c3; |
|
|
|
|
|
|
|
|
||
пt = 2 с. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
X = ? |
|
|
|
|
|
|
|
|
|
|
|
|
υ = ? |
|
|
|
|
|
|
|
|
|
|
|
|
a = ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
Решение
Координату Х найдем, подставив в уравнение движения числовые значения коэффициентов А, В, С и времени t:
Х = (2 +1 2 − 0,5 22 ) м = 0 .
|
Мгновенная скорость есть первая производная от координаты по |
У |
||||||||||||
времени: |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
υ = dХ = B + 3Ct2. |
|
Т |
|||||||
|
|
|
|
|
|
dt |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Н |
|
||
|
В момент времени t = 2 с |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
υ=1−3 0,5 23 = −5 м/с. |
Б |
|
|
|||||||
|
Ускорение точки найдем, взяв |
|
|
про зводную от скорости |
|
|||||||||
по времени: |
|
|
|
|
|
|
|
|
й |
|
|
|||
|
|
|
|
|
|
|
и |
|
|
|
||||
|
|
|
|
|
|
a = dυ |
|
|
|
|
||||
|
|
|
|
|
|
= 6 Ct. |
|
|
|
|
||||
|
|
|
|
|
|
|
|
первую |
|
|
|
|
||
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|||
|
В момент времени t = 2 с |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
т |
|
|
|
|
|
|
|
||
|
|
|
|
a = 6(−0,5) |
2 м/c2 = −6 м/c2. |
|
|
|
||||||
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
з |
|
Задача 1.2 |
|
|
|
|
|||||
|
|
о |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Т ло вращается вокруг неподвижной оси по закону ϕ = А+Вt+Сt2, |
|
||||||||||||
гдепА = 10 рад; В = 20 рад/с; С = –2 рад/с2. Найти полное ускорение |
|
|||||||||||||
точки, находящейся на расстоянии 0,1 м от оси вращения, для мо- |
|
|||||||||||||
|
времени t = 4 с. |
|
|
|
|
|
|
|
|
|
|
|||
мента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
Дано: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ = А + Вt + Сt2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
А = 10 рад; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
B = 20 рад/с; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
С = -2 рад/с2; |
|
|
|
|
|
|
|
|
|
|
|
|
У |
|||
|
|
r = 0,1 м; |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
t = 4 с. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
a = ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
Б |
|
||||
|
|
Полное ускорение а точки, |
|
|
|
|
|
|||||||||||
|
|
движущейся по кривой линии, мо- |
||||||||||||||||
|
|
жет быть найдено как геометрическая сумма тангенциального уско- |
||||||||||||||||
|
|
рения аrτ , направленного по касательной траекторииН, и нормально- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
|
йn |
|
|
|
|
го ускорения аn , направленного к центру кривизны траектории |
||||||||||||||||
|
|
(рис 1.1.): |
|
|
|
τ |
|
|
n взаимно |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
р |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
a = a |
|
+ a . |
|
|
|||
|
|
|
|
|
|
|
|
о |
|
|
τ |
n |
|
|
||||
|
|
Так как векторы а |
|
и |
а |
|
|
|
|
перпендикулярны, абсолют- |
||||||||
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
||||
|
|
ное значение ускорения |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
и |
|
|
|
a = |
a2 + a2 . |
|
(1.1) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Тангенц альное |
|
нормальное ускорения точки вращающегося |
||||||||||||||
|
|
тела выражаются формулами |
|
|
|
|
|
|
||||||||||
|
п |
з |
|
|
|
|
aτ = εr; an |
= ω2r , |
|
|
||||||||
где |
оω – угловая скорость тела; |
|
|
|
|
|
|
|||||||||||
Р |
|
|
ε |
– его угловое ускорение. |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
и |
r |
|
|
|
|
|
Подставляя выражение для аτ |
|
аn в формулу (1.1), находим |
||||||||||||||
|
|
|
|
|
|
a = |
|
|
ε2r2 + ω4r2 |
= r ε2 + ω4 . |
(1.2) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 |

Угловую скорость ω найдем, взяв производную угла поворота по времени:
|
|
|
|
|
|
ω = |
|
|
dϕ |
= B + 2Ct . |
|
|
|
||||
|
|
|
|
|
|
|
|
dt |
|
|
У |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
В момент времени t = 4 с угловая скорость |
|
|
||||||||||||||
|
|
|
ω = [20 + 2(−2) 4] рад/c = 4 рад/c. |
|
|||||||||||||
|
Угловое ускорение найдем, взяв первую производную от угло- |
||||||||||||||||
|
вой скорости по времени: |
|
|
|
|
|
|
|
Б |
Т |
|||||||
|
|
|
|
ε = |
dω |
= 2C = −4 |
рад/с2. |
|
Н |
||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
dt |
|
|
|
|
|
й |
|
|
||
|
Это выражение не содержит |
времени |
|
|
угловое |
||||||||||||
|
|
; следовательно, |
|||||||||||||||
|
ускорение заданного движения постоянно. |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
р |
ε заданное значение r в |
||||
|
Подставляя найденные значения ω |
||||||||||||||||
|
формулу (1.2), получим |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
т |
|
|
|
|
|
|
|||||
|
|
|
|
a =0,1 |
|
(−4)2 +44 =1,65 м/с2. |
|
|
|
||||||||
|
|
|
|
и |
оЗадача 1.3 |
|
|
|
|
||||||||
|
|
. |
з |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
При выстреле пруж нного пистолета вертикально вверх пуля |
||||||||||||||||
|
|
Дано |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
массой 20 г поднялась на высоту 5 м. Определить жесткость k пру- |
||||||||||||||||
|
жины пист лета, если она была сжата на 10 см. Массой пружины |
||||||||||||||||
|
пренебречь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
е |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m = 20 г = 0,02 кг; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h = 5 м; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = 10 см = 0,1 м. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
k = ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение
Воспользуемся законом сохранения энергии, но прежде проследим за энергетическими превращениями, с которыми связан выстрел.
При зарядке пистолета сжимается пружина и совершается работа А1
|
в результате чего пружина приобретает потенциальную энергиюП1 . |
|||||||||||
|
При выстреле потенциальная энергия пружины переходит в кинети- |
|||||||||||
|
ческую энергию T2 пули, а затем при подъеме ее на высоту h пре- |
|||||||||||
|
вращается в потенциальную энергию П2 |
пули. Если пренебречь по- |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
терями энергии в этой «цепочке» энергетических превращений, то на |
|||||||||||
|
основе закона сохранения энергии можно записать: |
|
Т |
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
А1 |
= П2 . |
|
|
Н |
(1.3) |
||
|
|
Найдем работу А1 . Сила F1, |
|
|
|
|
||||||
|
|
сжимающая пружину, является пе- |
||||||||||
|
|
|
|
|
|
|
|
Б |
|
|
||
|
ременной: в каждый момент она по направлению противоположна |
|||||||||||
|
силе упругости F и численно равна . С ла упругости, возникаю- |
|||||||||||
|
щая в пружине при ее деформац |
, определяется по закону Гука: |
||||||||||
|
|
|
|
|
|
ей |
|
|
|
|||
|
|
|
|
|
Fи= kx, |
|
|
|
|
|||
|
где х – абсолютная деф рмациярпружины. |
|
|
|
|
|||||||
|
|
Работу переменн й силы вычислим как сумму элементарных ра- |
||||||||||
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
бот. Элементарная рабо а при сжатии пружины на dx выразится |
|||||||||||
|
формулой |
|
т |
|
|
|
|
|
|
|||
|
|
|
|
и dA1 = F1dx . |
|
|
|
|
||||
|
|
|
з |
|
|
|
|
|
|
|
||
|
|
Интегрируя в пределах от 0 до х, получим |
|
|
|
|||||||
|
|
о |
|
|
|
|
|
|
|
|
||
|
п |
|
|
x |
1 kx2 |
x |
= 1 kx2 . |
|
|
|
||
|
|
|
A1= k ∫xdx = |
|
|
|
(1.4) |
|||||
е |
|
|
|
0 |
2 |
0 |
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|||||
Потенциальная энергия пули на высоте h определится по формуле |
||||||||||||
Р |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
25 |
||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
П2 = mgh , |
|
|
|
|
(1.5) |
||||
где g – ускорение свободного падения. |
|
|
|
|
|
|
||||||||||||
|
Подставив в (1.3) выражение А1 из (1.4) и П2 из (1.5), найдем |
У |
||||||||||||||||
|
|
|
|
|
|
|
|
1 |
kx2 = mgh , |
|
|
|
|
|||||
|
|
|
|
|
|
|
2 |
|
|
|
Т |
|||||||
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|||
|
|
|
|
|
|
|
|
|
k = 2 mgh . |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Б |
(1.6) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k. |
||
|
Проверим, дает ли полученная формула единицу жесткости |
|||||||||||||||||
Для этого в правую часть формулы (1.6) вместо величин подставим |
||||||||||||||||||
их единицы: |
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|||
[k ]= [m ][ g ][ h ] |
|
1 кг 1 м |
с- 2 |
м с- 2 |
|
|
|
|||||||||||
= |
1 м |
= 1 кг |
= 1 Н/м. |
|
||||||||||||||
|
[ x 2 ] |
|
|
|
|
|
|
|
р |
й1 м |
|
|
|
|||||
|
|
|
|
|
|
1 м2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
||||
|
Убедившись, что полученная единица Н/м является единицей |
|||||||||||||||||
жесткости, подставим в ф рмулу (1.6) значения величин и произве- |
||||||||||||||||||
дем вычисления: |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2 |
0,02 9,81 5 |
|
|
|
|
|
|
|
|||||
|
|
з |
т |
|
|
|
|
|
|
|
|
|
||||||
|
|
k |
= |
|
|
|
|
H/м |
=196 H/м. |
|
|
|
||||||
|
п |
|
|
|
|
(0,1)2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
Задача 1.4 |
|
|
|
|
|
|
||||||
Через |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
блокв |
|
виде сплошного |
диска, имеющего |
массу 80 г |
|||||||||||||
(рис. 1.2), ерекинута тонкая гибкая нить, к концам которой подве- |
||||||||||||||||||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ш ны грузы с массами 100 и 200 г. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением и массой нити пренебречь.
26
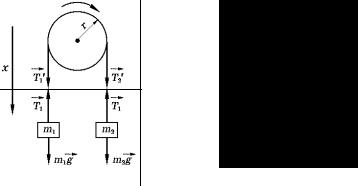
Дано:
m = 80 г = 0,08 кг;
m1 = 100 г = 0,1 кг; m2 = 200 г = 0,2 кг.
а = ?
|
|
|
|
|
|
|
|
|
Рис. 1.2 |
Н |
У |
||
|
|
|
|
|
Решение |
|
Б |
Т |
|||||
|
|
Воспользуемся основными уравнениями динамики поступатель- |
|||||||||||
|
ного и вращательного движений. Для этого рассмотрим силы, дей- |
||||||||||||
|
|
|
|
|
|
|
|
й |
|
|
|
||
|
ствующие на каждый груз в отдельности и на блок. На первый груз |
||||||||||||
|
|
|
|
|
|
эти |
|
|
|
|
|||
|
действуют две силы: сила тяжести |
m1g |
и сила упругости (сила на- |
||||||||||
|
тяжения нити) T1. Спроектируем |
|
с лы на ось Х, которую напра- |
||||||||||
|
|
|
|
|
р |
|
|
|
|
|
|
||
|
вим вертикально вниз, и нап шем у авнение движения (2-й закон |
||||||||||||
|
Ньютона): |
о |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
= −m1a . |
|
|
|
(1.7) |
||||
|
|
|
|
т |
|
|
|
|
|||||
|
|
|
движения |
m1g −T1 |
|
|
|
||||||
|
|
|
m2 g −T2 |
= −m2a. |
|
|
|
(1.8) |
|||||
|
|
Уравнение |
|
для второго груза запишется аналогично: |
|||||||||
|
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
относительно оси, |
|||
|
|
П д действием двух моментов сил T1r и T2r |
|||||||||||
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
ер ендикулярной плоскости чертежа, блок приобретает угловое |
||||||||||||
|
уск рение |
|
|
|
|
|
|
|
|
|
|
||
е |
|
|
|
ε = a . |
|
|
|
|
|
|
|||
Р |
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Согласно основному уравнению динамики вращательного движения,
27
|
|
|
|
|
|
T ′2 r − T 1′ r = J z ε, |
|
|
|
(1.9) |
|
|||||||
где J z = |
1 |
mr2 – момент инерции блока (сплошного диска) отно- |
|
|||||||||||||||
|
|
|||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сительно оси z. |
|
|
|
|
|
|
|
|
|
|
|
|
У |
|||||
|
Согласно 3-му закону Ньютона, с учетом невесомости нити |
|
||||||||||||||||
|
|
|
|
|
|
T1′ = T1; T2′ = T2 . |
|
|
|
|
||||||||
|
Воспользовавшись этим, подставим в уравнение (1.9) вместо T1′ |
|||||||||||||||||
|
|
|||||||||||||||||
и T2′ выражения Т1 и Т2, получив их предварительно из уравненийТ |
||||||||||||||||||
(1.7) и (1.8): |
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
||||
|
|
|
(m g −m a) r −(m g +m a) r = mr2a /(2r). |
|
||||||||||||||
|
|
|
|
2 |
2 |
|
1 |
|
|
1 |
|
|
|
Б |
|
|
||
|
После сокращения на r и перегрупп |
|
|
|
|
|
||||||||||||
|
|
|
членов найдем |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
m2 −m1 |
й |
|
|
|
||||||
|
|
|
|
|
|
a = |
|
|
g. |
|
|
|
(1.10) |
|
||||
|
|
|
|
|
|
m |
+m |
+m / 2 |
|
|
|
|
||||||
|
|
|
|
|
|
2 |
|
1 |
ровки |
|
|
|
|
|||||
|
Формула (1.10) |
|
массырвыразить в граммах, как они да- |
|
||||||||||||||
ны в условии задачи, а уск рение – в единицах СИ. После подста- |
|
|||||||||||||||||
новки числовых значен й вформулу |
(1.10) получим |
|
|
|
||||||||||||||
|
|
|
|
|
|
позволяет |
|
|
|
|
|
|
|
|
|
|
||
|
|
a = |
|
|
(200 −100) г |
|
9,81 м/c2 |
= 2,88 м/c2. |
|
|
||||||||
|
|
|
(200и+100 + 80/2) г |
|
|
|||||||||||||
|
|
|
з |
|
|
|
1.5 |
|
|
|
|
|
|
|
||||
|
о |
Задача |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Платформа в виде сплошного диска радиусом 1,5 м и массой |
|
||||||||||||||||
180пкг вращается по инерции около вертикальной оси с частотой |
|
|||||||||||||||||
10 об/мин. В центре платформы стоит человек массой 60 кг. Какую |
|
|||||||||||||||||
линейную скорость относительно пола помещения будет иметь че- |
|
|||||||||||||||||
ловек, если он перейдет на край платформы? |
|
|
|
|
|
|||||||||||||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
Дано: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R = 1,5 м; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
m = 180 кг; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
n = 10 об/мин = 1/6 об/c. |
|
|
|
|
|
|
|
|
|
|||||||
|
|
υ = ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
Т |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Платформа вращается по инерции. Следовательно, момент внеш- |
|||||||||||||||
|
|
них сил относительно оси вращения, совпадающей с геометриче- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|
|
|
ской осью платформы, равен нулю. При этом условии моментУим- |
||||||||||||||||
|
|
пульса Lz системы платформа – человек остается постоянным: |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
Lz = J zω = const , |
|
|
(1.11) |
||||||
|
|
где Jz – момент инерции платформы с человеком относительно оси |
||||||||||||||||
|
|
вращения; |
|
|
|
|
|
|
|
|
й |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
||||
|
|
|
ω – угловая скорость платформы. |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|||
|
|
|
Момент инерции системы равен сумме моментов инерции тел, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
рмы |
|
|
|
|
|
|||
|
|
входящих в состав системы, поэтому |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
J z = J1 + J2 , |
|
|
|
||||
|
|
|
|
|
|
|
|
|
о |
|
; |
|
|
|
|
|
||
|
|
где J1 – момент инерции платф |
|
|
|
|
|
|
||||||||||
|
|
|
J2 |
– момент инерции чел века. |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
С учетом этого равенс ва (1.11) примет вид |
|
|
|||||||||||||
|
|
|
|
|
з |
т( J |
+ J |
2 |
)ω = const |
|
|
|
||||||
|
|
|
о |
|
|
|
1 |
|
|
|
|
|
|
|
||||
|
|
или |
|
|
|
|
|
|
|
|
|
|
′ |
′ |
′ |
|
(1.12) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
п |
|
|
|
|
(J1 + J2 )ω = (J1 |
+ J2 )ω, |
|
||||||||||
|
|
где значения моментов инерции J1 и J2 относятся к начальному со- |
||||||||||||||||
е |
|
|
|
|
|
J1′, J2′ |
|
|
1 |
|
|
|
|
|
||||
Р |
|
стоянию системы, |
– к конечному. Момент инерции плат- |
|||||||||||||||
формы относительно оси вращения Z при переходе человека не из- м няется:
J1 = J ′ = 2 m1R2 .
29

Момент инерции человека относительно той же оси будет изменяться. Если рассматривать человека как материальную точку, то его момент инерции J2 в начальном положении (в центре платформы) можно считать равным нулю. В конечном положении (на краю платформы) момент инерции человека
|
|
|
|
|
|
|
|
|
J 2′ |
= m2 R2 . |
|
|
|
|
|
|
|
|
У |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
|
|
Подставим в формулу (1.12) найденные выражения моментов |
|
||||||||||||||||||||||
инерции, а также выразим начальную угловую скорость ω враще- |
|
|||||||||||||||||||||||
ния платформы с человеком через частоту вращения n ( ω = 2πn ) и |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
′ |
|
– через линейную скорость υ чело- |
|
||||||||||||
конечную угловую скорость ω |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
Б |
|
|
|||||
века относительно пола ω = υ/ R : |
|
|
|
|
|
|
|
|
Н |
|
||||||||||||||
|
|
1 |
m R2 |
|
|
|
|
|
1 |
|
|
2 + m R2 |
υ |
|
|
|||||||||
|
|
|
|
+ 0 2πn = |
|
m R |
|
|
. |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
й |
|
|
|
|
||||
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
R |
|
|
|
|
|||||
|
После сокращения на R2 и простых преобразований находим ин- |
|
||||||||||||||||||||||
тересующую нас скорость: |
|
|
р |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
υ = |
2πnR |
|
|
и. |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
т |
|
|
|
m1 + 2m2 |
|
|
|
|
|
|
|
||||||
|
Подставим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
значения физических величин в СИ и про- |
|
||||||||||||||||||
|
|
|
|
числовые |
о |
|
|
|
|
|
|
|
|
|
|
|||||||||
изведем вычислен я: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
з |
|
1 |
|
|
|
|
|
180 |
|
м/c = 1 м/c. |
|
|
|
|||||||||
|
υ = |
2 3,14 |
1,5 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
п |
|
|
|
|
|
|
6 |
|
|
180 |
|
+ 2 |
60 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Задача 1.6 |
|
|
|
|
|
|
|
|||||||||
ние |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Рак таоустановлена на поверхности Земли для запуска в верти- |
|
||||||||||||||||||||||
кальном на равлении. При какой минимальной скорости υ1, сооб- |
|
|||||||||||||||||||||||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щ нной ракете при запуске, она удалится от поверхности на расстоя- , равное радиусу Земли (R = 6,37 106 м)? Всеми силами, кроме силы гравитационного взаимодействия ракеты и Земли, пренебречь.
30
