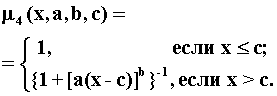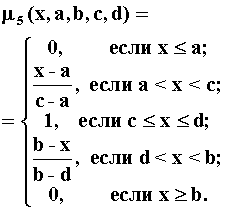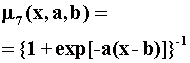2.3.2 Метод иерархий Саати

Метод анализа иерархий (МАИ), предложенный Т.Л. Саати, основан на парных сравнениях альтернативных вариантов по различным критериям с использованием девятибалльной шкалы и последующим ранжированием набора альтернатив по всем критериям и целям. Взаимоотношения между критериями учитываются путем построения иерархии критериев и применением парных сравнений для выявления важности критериев и подкритериев.

К основным процедурам метода анализа иерархий относятся следующие:

- генерация множества альтернативных вариантов;

- формирование множества критериев для оценки альтернативных вариантов и представление его в виде иерархии;

- выявление предпочтений экспертов на множестве альтернатив по различным критериям;

- установление относительной важности влияния критериев на общую цель и другие критерии;

- получение ранжированных наборов альтернатив по всем критериям и целям.

Все оценки определяются экспертами. Сначала эксперты генерируется множество допустимых альтернатив, среди которых необходимо провести выбор лучшей альтернативы или упорядочивание всех элементов.

Вершиной иерархий обычно является глобальная цель, на следующих уровнях присутствуют критерии и на самом нижнем уровне - альтернативы.

Иерархическая структура критериев и целей является моделью знаний конкретной предметной области, которая изменяется и уточняется с течением времени.

Элементы одного уровня иерархии попарно сравниваются по силе их влияния на элементы более высокого уровня. Результаты заносятся в матрицу попарных сравнений. При сравнении элемента с самим собой имеем равную значительность «1», т.е. главная диагональ матрицы состоит из единиц. В МАИ используется 9-балльная шкала вида:

Интенсивности относительной важности	Определение	Объяснение
1	Равная важность	Равный вклад двух объектов в достижении цели
3	Умеренное превосходство одного над другим	Опыт и суждения дают легкое превосходство одному объекту над другим
5	Существенное или сильное превосходство	Опыт и суждения дают сильное превосходство одному объекту над другим
7	Значительное превосходство	Одному объекту дается настолько сильное превосходство над другим, что оно становится значимым
9	Очень сильное превосходство	Очевидность превосходства одного объекта над другим подтверждается наиболее сильно
2,4,6,8	Промежуточные значения между двумя соседними суждениями	Принимаются в компромиссных случаях
Обратные величины приведенных чисел	Если при сравнении одного объекта с другим получено одно из вышеуказанных чисел (например 3), то при сравнении второго объекта с первым получим обратную величину (т.е.1/3)

Следующий шаг состоит в вычислении вектора приоритетов по данной матрице. Существует несколько методов оценки этого вектора. Например, суммировать элементы каждой строки матрицы и нормировать делением каждой суммы на сумму всех элементов матрицы. Первый элемент результирующего вектора будет приоритетом первого объекта, второй - второго объекта и т.д.

В общем случае (при наличии более трех уровней) иерархия оценивается следующим образом:

1. Производится попарное сравнение элементов 2-го уровня по степени влияния на выполнение цели. Результаты заносятся в матрицу попарных сравнений A₁;

2. Производится попарное сравнение элементов 3-го уровня по степени влияния на каждый критерий 2-го уровня. Результаты заносятся в n₁ (n₁ - количество критериев) матриц попарных сравнений A₁₁...A_n1;

3. Действия п.2 повторяются для всех оставшихся уровней (если они есть);

4. Для каждой матрицы вычисляется вектор приоритетов;

5. Каждый элемент вектора приоритетов 2-го уровня умножается на соответствующий элемент вектора приоритетов каждой из матриц (A₁₁...A_n1). После сложения всех произведений получается вектор приоритетов 3-го уровня;

6. Действия п.5 выполняются для всех оставшихся уровней.

В результате получается вектор приоритетов n-го уровня по степени влияния на выполнение цели.

Уровень цели

Цель

5. Месторасположение

4. Коллектив

3. Доход

2. Интересно

1. Рост

Уровень критериев Вектор приоритетов (0,4; 0,15; 0,25; 0,1; 0,1)

А

Б

В

Уровень альтернатив

Матрицы попарных сравнений альтернатив имеют вид (всего их 5 – по количеству критериев, для каждого критерия своя матрица):

	А	Б	В
А	1
Б		1
В			1

Векторы приоритетов альтернатив:

По критерию 1 – (0,5; 0,3; 0,2)

По критерию 2 – (0,4; 0,4; 0,2)

По критерию 3 – (0,3; 0,3; 0,4)

По критерию 4 – (0,2; 0,3; 0,5)

По критерию 5 – (0,1; 0,3; 0,6)

По влиянию на цель – (0, 365; 0,315; 0,31) Выбирается альтернатива А

0,4×0,5+0,15×0,4 + 0,25×0,3 + 0,1×0,2 + 0,1×0,1 = 0,365

0,4×0,3+ 0,15×0,4+ 0,25×0,3+ 0,1×0.3+ 0,1×0,3 = 0,315

0,4×0,2+ 0,15×0,2+ 0,25×0,4+ 0,1×0,5+0,1×0,6 = 0,32

В рамках МАИ нет общих правил для формирования структуры модели принятия решения. Это является отражением реальной ситуации, поскольку всегда для одной и той же проблемы имеется целый спектр мнений. Метод позволяет учесть это обстоятельство с помощью построения дополнительной модели для согласования различных мнений, посредством определения их приоритетов. Таким образом, метод позволяет учитывать «человеческий фактор» при подготовке принятия решения. Это одно из важных достоинств данного метода перед другими методами принятия решений.

Формирование структуры модели принятия решения в МАИ достаточно трудоемкий процесс. Однако в итоге удается получить детальное представление о том, как именно взаимодействуют факторы, влияющие на приоритеты альтернативных решений, и сами решения. Как именно формируются рейтинги возможных решений и рейтинги, отражающие важность факторов.

В рамках МАИ нет средств для проверки достоверности данных. Этот недостаток ограничивает отчасти возможности применения метода. Однако метод применяется главным образом в тех случаях, когда в принципе не может быть объективных данных, а ведущими мотивами для принятия решения являются предпочтения людей.

Работа по подготовке принятия решений часто является слишком трудоемкой для одного человека. Однако применение метода позволяет разбить большую задачу, на ряд малых самостоятельных задач. Благодаря этому для подготовки принятия решения можно привлечь экспертов, работающих независимо друг от друга над локальными задачами.

Метод дает только способ рейтингования альтернатив, но не имеет внутренних средств для интерпретации рейтингов, т.е. считается, что ЛПР, зная рейтинг возможных решений, должен в зависимости от ситуации сам сделать вывод. Это следует признать недостатком метода.

Метод дает удобные средства учета экспертной информации для решения различных задач. Он отражает естественный ход человеческого мышления и дает не только способ выявления наиболее предпочтительного решения, но и позволяет количественно выразить степень предпочтительности по средством рейтингования. Это способствует полному и адекватному выявлению предпочтений ЛПР. Кроме того, оценка меры противоречивости использованных данных позволяет установить степень доверия к полученному результату.

Примечание. Упомянутая в 2.3.2 схема оценки альтернативы по совокупности оценок ее эффективности для множества частных критериев может использоваться в рамках других МПР как самостоятельный алгоритм принятия решения на основе линейной свертки оценок по частным критериям:

1. Для каждой допустимой альтернативы A₁,…,A_n оценить степень удовлетворения ею каждого из частных критериев К₁,…,К_m в единой балльной шкале. В результате получаем матрицу оценок вида

с₁₁,…,с_1m

^{…………..}

с_n1,…,с_nm

где с_ij, 1≤i≤n, 1≤j≤m – оценка степени выполнения критерия К_j в случае выбора альтернативы A_i

2. Оценить относительную важность (построить веса) критериев

р₁,…,р_m

3 Для каждой из альтернатив A_i, i=1,…,n оценить степень удовлетворения ею общей цели ЗПР как взвешенное среднее вида

3 В качестве решения выбрать ту альтернативу, которой соответствует максимальная оценка

2.3.3 Нечеткое множество и функция принадлежности

Построение моделей автоматизации процесса принятия решений для задач управления на основе экспертной информации, имеющих нечеткое описание, базируется на понятиях «нечеткое множество» и «лингвистическая переменная».

2.3.3.1 Коротко остановимся на понятии лингвистической переменной. Не вдаваясь в тонкости, ее можно определить как переменную, значениями (термами) которой являются не числа, а слова или предложения естественного (или формального) языка. Например, лингвистическая переменная "возраст" может принимать следующие значения: очень молодой, молодой, среднего возраста, старый, очень старый и другие - в зависимости от требуемой степени детальности описания. Ясно, что переменная "возраст" будет обычной переменной, если ее значения - точные числа; лингвистической она становится будучи использована в нечетких рассуждениях человека.

Каждому терму лингвистической переменной соответствует определенное нечеткое множество со своей функцией принадлежности, которая описывает совместимость этого терма с различными числовыми значениями.

Пример возможного соответствия значений лингвистической переменной «оценка» количественным интервальным значениям

Лингвистическая оценка	Отметки на шкале желательности
Очень хорошо	1.00 - 0.80
Хорошо	0.80 - 0.63
Удовлетворительно	0.63 - 0.37
Плохо	0.37 - 0.20
Очень плохо	0.20 - 0.00

Более детально с понятием лингвистической переменной и многочисленными примерами можно познакомиться в книге Заде, Л.А. Понятие лингвистической переменной и его применение к понятию приближенных решений / Л.А. Заде. – М.: Мир, 1976.

2.3.3.2 В обычной теории множеств существуют несколько способов задания множества. Одним из них является задание с помощью характеристической функции, определяемой следующим образом. Пусть U - так называемое универсальное множество, из элементов которого образованы все остальные множества, рассматриваемые в настоящей задаче, например множество всех целых или действительных чисел и т.д. Характеристическая функция подмножества A  U - это функция mA, значения которой указывают, является ли элемент x из U элементом множества A. В классической теории множеств эта функция принимает два значения: mA(х)=0 (х не является элементом А) и mA(х)=1 (х является элементом А).

С точки зрения характеристической функции нечеткие множества являются естественным обобщением обычных множеств, когда мы отказываемся от бинарного характера этой функции и предполагаем, что она может принимать любые значения из отрезка [0, 1]. В теории нечетких множеств характеристическая функция называется функцией принадлежности, а ее значение mA(x) - степенью принадлежности элемента x нечеткому множеству A.

В результате нечеткое множество определяется набором пар {(x; mA(x))}, где mA - функция принадлежности

Например, запись A = {(a; 0), (b; 0,1), (c; 0,5), (d; 0,9), (e; 1)} может трактоваться следующим образом: элемент a не принадлежит множеству A, элемент b принадлежит ему в малой степени, элемент c более или менее принадлежит, элемент d принадлежит в значительной степени, e является элементом A.

Потребность в таких множествах часто возникает при рассмотрении плохоформализуемых свойств и понятий. Например, как формализовать понятие «молодой человек». Не будешь же людей младше 25 четко причислять к числу молодых, а людей старше 25 четко не причислять к молодым. Если через М обозначить множество молодых людей, то разумнее, например, принять градацию типа mМ(x)=1 для людей младше 25 лет, mМ(x)=0,8 для людей младше 30 лет, mМ(x)=0 для людей старше 50 лет и т.д.

Конкретный вид функций принадлежности определяется на основе различных дополнительных предположений о свойствах этих функций (симметричность, монотонность, непрерывность первой производной и т.д.) с учетом специфики имеющейся неопределенности, реальной ситуации на объекте и числа степеней свободы в функциональной зависимости. Вид данной функции носит в значительной мере субъективный характер. Уменьшить степень этой субъективности можно, используя метод экспертных оценок, суть которого состоит в том, что как вид функции принадлежности, так и значения соответствующих параметров являются результатом коллективного творчества группы специалистов в рассматриваемой области - экспертов.

Во многих практических ситуациях функция принадлежности должна быть оценена исходя из частичной информации о ней, скажем такой, как значения, принимаемые ею на конечном множестве опорных точек х₁,...,х_n. В этом случае говорят, что она частично определена с помощью "поясняющего примера".

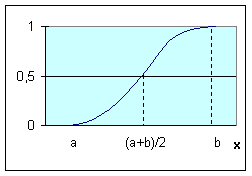
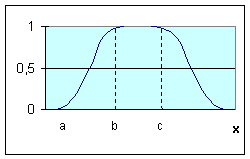
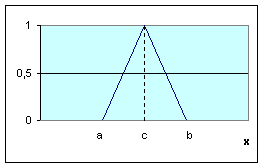
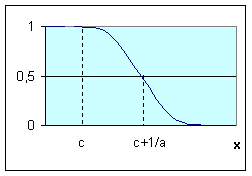
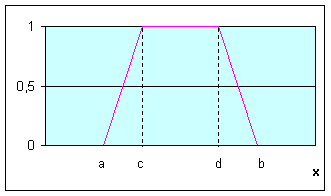
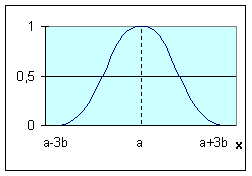
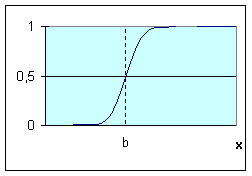
На рис. приведены все основные виды функций принадлежности, применяемые в теории нечетких множеств.

Рис.4.1. Примеры различных способов построения функций принадлежности.

 

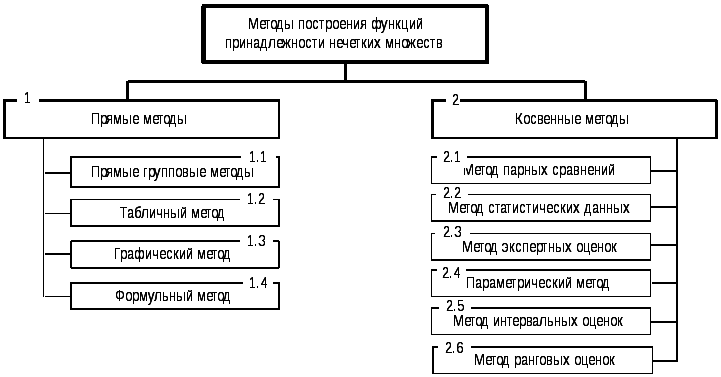
 Рисунок – Классификация методов построения функций принадлежности нечетких множеств

Прямые методы характеризуются тем, что эксперт непосредственно задает правила определения значений функции принадлежности μ_А(х), характеризующей элемент х.

Эти значения согласуются с его предпочтениями на множестве элементов Х следующим образом:

1. Для любых х₁, х₂ Î Х μ_А(х₁) < μ_А(х₂) тогда и только тогда, когда х₂ предпочтительнее х₁, т.е. в большей степени характеризуется свойством А;

2. Для любых х₁, х₂ Î Х μ_А(х₁) = μ_А(х₂) тогда и только тогда, когда х₁ и х₂ безразличны относительно свойства А.

Как правило, прямые методы задания функции принадлежности используются для измеримых понятий, таких как скорость, время, расстояние, давление, температура и т.д., или когда выделяются полярные значения.

Разновидностями прямых методов являются прямые групповые методы, когда, например, группе экспертов предъявляют конкретный объект, и каждый должен дать один из двух ответов: принадлежит или нет этот объект к заданному множеству. Тогда число утвердительных ответов, деленное на общее число экспертов, дает значение функции принадлежности объекта к данному нечеткому множеству.

Прямыми методами являются также непосредственное задание функции принадлежности таблицей, графиком или формулой.

Из анализа результатов исследований и решения практических задач, связанных с необходимостью обрабатывать информацию, известно, что прямые методы в основном используются в качестве вспомогательных, т. к. характеризуются большой долей субъективизма.

Косвенные методы построения значений функции принадлежности используются в случаях, когда нет элементарных измеримых свойств, через которые определяются нечеткие множества.

В косвенных методах значения функции принадлежности выбираются таким образом, чтобы удовлетворить заранее сформулированным условиям. Экспертная информация является только исходной информацией для дальнейшей обработки. Дополнительные условия могут налагаться как на вид получаемой информации, так и на процедуру ее обработки. К таким методам относятся статистический метод, метод парных сравнений, метод экспертных оценок и ряд других. Например, метод построения функции принадлежности на основе парных сравнений основан на обработке матриц оценок, отражающих мнение эксперта об относительной принадлежности элементов множеству или степени выраженности у них свойства, формализуемого множеством. Метод статистических данных основан на обработке статистической информации. В качестве степени принадлежности элемента множеству принимается оценка частоты использования понятия, задаваемого нечетким множеством, для характеристики элемента.

На универсальной шкале [0, 1] необходимо разместить значения лингвистической переменной: ОЧЕНЬ МАЛО, МАЛО, СРЕДНЕ, МНОГО, ОЧЕНЬ МНОГО. Тогда степень принадлежности некоторого значения вычисляется как отношение числа экспериментов, в которых оно встречалось в определенном интервале шкалы, к максимальному для этого значения числу экспериментов по всем интервалам. Метод основывается на условии, что в каждый интервал шкалы попадает одинаковое число экспериментов. Это условие часто не соблюдается. В реальных случаях составляется эмпирическая таблица, в которой эксперименты могут быть распределены неравномерно по интервалам, а в некоторые интервалы могут вообще не попасть.

Данный метод может быть использован для формализации задачи выбора альтернатив, т. к. эксперты могут определить конкретное множество допустимых альтернатив и удалить не нужные. В данном случае оценки отдельных экспертов можно рассматривать как независимые реализации случайной величины.

Построение функции принадлежности на основе экспертных оценок - данный метод построения функций принадлежности основан на использовании нечетких чисел, приблизительно равных некоторому четкому числу, и приближенных интервальных оценок, отражающих мнения экспертов по рассматриваемому вопросу. Задача сводится к отысканию параметров заранее заданной (экспоненциальной) функции, при решении которой используются результаты экспертного опроса. Этот метод часто целесообразнее всего использовать при решении задач выработки и оценки альтернатив.

Построение функций принадлежности на основе интервальных оценок. Данный метод применяется для формализованного представления задач выбора, в которых отсутствует четкая грань между допустимым и недопустимым (в пространстве неуправляемых параметров) и между идеальным и неудовлетворительным состояниями (в пространстве критериев).