Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

metodichkaFTUG_chast2

.pdf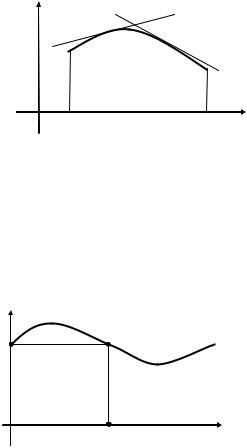

Скачиваний:

Добавлен:

26.03.2016

Размер:

1.82 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 119 10 11 > Следующая >>>

вверх) на (a, b), если дуга кривой y f (x) на этом интервале

расположена ниже любой касательной, проведенной к графику этой функции (рис. 6.5).

				y f (x)
		0	a		b	x
		0	a		b
				Рис. 6.5
Теорема 7.		Если функция f(x) дважды				дифференцируема на
				всюду на этом интервале, то график
(a, b) и f (x)		0 f (x) 0		всюду на этом интервале, то график
функции вогнутый (выпуклый) на (a, b).
Точка	x0	такая,	что	график функции y f (x)			меняет
выпуклость	на	вогнутость		или наоборот,	проходя через		точку

x0 , f (x0 ) , называется точкой перегиба (рис. 6.6).

M0 x0, f (x0 )

y f (x)

Рис. 6.6

Для нахождения точек перегиба вначале находят критические точки 2-го рода – те значения x, для которых f (x) 0 или f (x)

не существует. Далее используют достаточные условия существования точек перегиба.

Теорема 8 (первый признак перегиба). Если функция f(x)

130

непрерывна в критической точке 2-го рода x0 и ее вторая производная

f (x) имеет различные знаки слева и справа от точки x0 ,	то точка x0
– точка перегиба.
Теорема 9 (второй признак перегиба). Если функция f(x) имеет
непрерывную производную f (x) в точке x0 ,	в которой

f (x0 ) 0, f '''(x0 ) 0, то x0 – точка перегиба.

Замечание 2. При исследовании функции и построении ее графика целесообразно использовать первый признак перегиба, так как одновременно получаем возможность исследования графика функции на выпуклость и вогнутость.

Пример 1. Найти экстремумы функции y x e1 2 x2 .

Решение. Подозрительными на экстремумы точками будут те, в которых производная функции либо равна нулю, либо не существует.

Найдем производную функции:

y ( x e1 2x2 ) (x) e1 2x2 ( x)(e1 2x2 )e1 2x2 x e1 2x2 ( 4x) e1 2x2 ( 1 4x2 ).

Она определена для любого x R. Приравняем производную к нулю:

e1 x2 ( 1 4x2 ) 0, значит,

1 4x2

0. Решая это уравнение, получим

x 12 . Областью определения функции является числовая прямая.

Исследуем функцию на экстремум в этих точках тремя способами.

1-й способ. Воспользовавшись теоремой 3, исследуем поведение

		1		1		1		1
функции на промежутках	,		,		,		,		, .
функции на промежутках	,		,		,		,		, .
		2		2		2		2

Для этого	определим		знак	производной,			т. е.	выражения
e1 2 x2 ( 1 4x2 ).	Очевидно,		что для всякого			x R		выполняется
неравенство e1 2 x2	0. Поэтому знак выражения					f (x)	зависит от знака
квадратичного выражения 4x2 1 (рис. 6.7).
					f (x)
+				+
	1		–	1		x

		2		2				131
								131

Рис. 6.7

Так как при «переходе» через точку с абсциссой x 12 производная y меняет знак с «+» на «–», то, согласно теореме 1, в этой точке функция

достигает максимума.
При «переходе» через точку															x				1		производная y							меняет знак с «–»
При «переходе» через точку															x						производная y							меняет знак с «–»
																		2
на «+». Поэтому в данной точке функция достигает минимума.
2-й способ. Воспользуемся теоремой 4 и вычислим вторую
производную функции:
y " e1 2 x2 ( 1 4x2 ) ' 2 2x e1 2 x2 ( 1 4x2 ) e1 2 x2 8x
e1 2 x2 4x 16x3 8x .
Вычислим ее значение в критических точках																									x		1	и x	1	:
																										2		2
							1 2																3					1
		1		1 2								1								1					1
							2
							2
y "				e				4					16											8		4e2 0.
y "				e				4					16											8		4e2 0.
		2										2								2					2

Согласно теореме 4, в точке														x				1		функция достигает максимума.
Согласно теореме 4, в точке														x				2		функция достигает максимума.
																		2
				1	1 2										3									1
	1				2	2				1		1								1
	1				2	2				1		1								1
y "			e				4				16					8							4e2 0.
y "			e				4				16					8							4e2 0.
	2									2		2								2

Согласно теореме 4 в точке x																	1		функция достигает минимума.
Согласно теореме 4 в точке x																2			функция достигает минимума.
																2
3-й способ. Воспользуемся теоремой 5. Так как производная первого
порядка	в точке					x			1		равна			нулю,								а	производная					второго			(четного)
порядка	в точке					x		2			равна			нулю,								а	производная					второго			(четного)
								2
порядка в этой точке меньше нуля, то, согласно теореме 5, x																															1	– точка
порядка в этой точке меньше нуля, то, согласно теореме 5, x																														2		– точка
																														2
локального максимума. В точке														x				1		производная первого порядка также
локального максимума. В точке														x				2		производная первого порядка также
																		2
равна нулю, а производная второго																					(четного) порядка больше нуля.
132

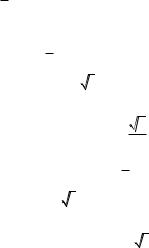
Следовательно, точка x 12 – точка локального минимума.

Вычислим максимум и минимум функции. Максимум функции равен значению функции в точке x0 12 :


	1	1		1 2 12 2	1	1 12		e
y			e			e			.
y			e		2	e	2		.
	2	2			2		2

Итак, локальный максимум функции равен 2e .

Вычислим значение функции в точке x0 12 :

	1	1	1 2	1	2	1	1 12		e
				2
y			e				e			.

	2	2				2		2

Итак, локальный минимум функции равен

Пример

Найти наибольшее

и наименьшее

значения функции

на отрезке [–2, 2].

x x2 1

Решение. Найдем точки, которые будут подозрительными на

экстремум. Для этого вычислим производную функции

y (x)

x (x x2 1) x(x x2

x x2

1 x(1 2x)

(x x2 1)2

x2 1)2

x x2

1 x 2x2

x2 1

(x x2 1)2

(x2 x

1)2

Производная существует во всех точках

x R. Найдем критические

точки.

Полагаем

y (x) 0,

т. е.

x2 1 0.

Получаем

x 1. Обе точки

x 1

принадлежат интервалу (–2,

2). Поэтому, будем искать

значение функции в этих точках и на концах отрезка. Вычисляем:

f ( 2)

;

f ( 1)

;

f (1)

2 4 1

1 1 1 3

1 1

f (2)

2 4 1

Выбрав

среди

полученных

значений

наибольшее и наименьшее,

133

получаем: y

y(1)

1, y

y( 1)

наим.

наиб.

Пример 3.

Дана

функция

6x. Вычислить

4m M, где m и M – соответственно наименьшее и наибольшее значения функции.

Решение. Найдем производную функции:

x		5	3		11
x			3	x4 x3	11	x2		x4 3x3 3x2 11x 6.
y							6x
y							6x
	5		4		2
	5		4		2

Разложив полученное выражение на множители, получим: y (x 1)2 (x 2)(x 3).

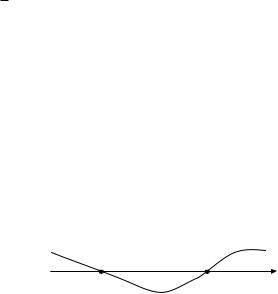
Поскольку функция задана на всей числовой оси (не на отрезке), то исследуем производную на знак методом интервалов (рис. 6.8).

	+						+
	+
		–2	–	1	–	3	x
				Рис. 6.8
В окрестности точки x 2 выполняется условие
f		x ( ; 2),
f	(x) 0,	x ( ; 2),
	(x) 0,	x ( 2;1).
f	(x) 0,	x ( 2;1).
Поэтому, согласно теореме 3 (первый признак экстремума функции),
x 2 – точка локального максимума.
В	окрестностях		точки x 1	производная		y всюду	отрицательна.
Поэтому в точке x 1 экстремума нет.
В окрестности точки x 3 выполняется условие
f		x (1;3),
f	(x) 0,	x (1;3),
	(x) 0,	x (3; ).
f	(x) 0,	x (3; ).

Поэтому x 3 – точка локального минимума.

Найдем значения функции в точках минимума и максимума:

m f (3)	273	;	M f ( 2)	118	.
	20			5

Иных точек локального минимума и максимума функция не имеет.

134

Искомая величина равна 4m M 4 273 118 155 31. 20 5 5

Пример 4. Найти точки перегиба функции y ln x 1x .

Решение. Для данной функции найдем критические точки 2-го рода. Для этого найдем производную 2-го порядка заданной функции:

x 1

y '

ln x

;

x 1

x 1 ' x

' x 1

2x(x 1)

y ''

x x 2x 2

2 x

В точке

x 2

полученная

производная

f (x) 0,

производная

f (x)

не существует. Поэтому точки x 2

а в точке x 0 и x 0 являются

критическими точками 2-го рода.

Исследуем функцию на перегиб несколькими способами.

1-й способ. Воспользуемся теоремой 8 (первым признаком перегиба). Исследуем вторую производную на знак методом интервалов (рис. 6.9).

				+
	–	0		2	–	x
	–	0		2	–
				Рис. 6.9
В окрестности точки x 0 выполняется условие:
f "(x) 0,	x ( ;0),
	x (0; 2).
f "(x) 0,	x (0; 2).
Поэтому, согласно теореме 8,				x 0 – точка перегиба функции.
В окрестности точки x 2 выполняется условие:
f "(x) 0,	x (0; 2),		Поэтому x 2 – точка перегиба.
			Поэтому x 2 – точка перегиба.
f (x) 0,	x (2; ).

2-й способ: Воспользуемся теоремой 9 (второй признак перегиба). Вычислим:

135

	2 x			2 x x3 x3 2 x						x	3	3x		2	(2	x)			2x 6
y (x)	2 x									x		3x			(2	x)			2x 6		.
y (x)									2				6								.
		3						x3	2				6							4
	x							x3				x							x
Вычислим значение этой производной в точке x 2,																где	f (x) 0 :
y (2)			2 2 6		1		0.
y (2)							0.
			24	8
Согласно теореме 9 в точке x 2 функция имеет перегиб.
В точке			x 0 заданная функция не определена,											однако слева и справа
от нее имеет различный характер выпуклости.
Вычислим значение функции в точке x 2 : y(2) ln 2																	1	.
Вычислим значение функции в точке x 2 : y(2) ln 2																	2	.
																	2
						1
Получили 2; ln 2								– точка перегиба.
Получили 2; ln 2								– точка перегиба.
						2

Задания для решения в аудитории

I уровень

1.1. Найдите критические точки функции:

1) y 3x3 27x ; 2)	y 2xex ; 3)	y	x3	; 4) y x5	5x4	5x3 1.
			x2
		3

1.2. Найдите для данных функций точки экстремума, интервалы возрастания и убывания:

1)	y	x4	2x3			11	x2	6x;	2)	y		x5			x4		x3 ;
		4				2					5			2
				1	2						1		e x e			x
3)	y	x			;				4)	y
3)	y	x			;				4)	y
				x							2

1.3. Найдите наибольшее и наименьшее значения функции на промежутке:

x2 3, x 2; 2 ;

2) y

1, x 1; 4 ;

1.4. Найдите интервалы выпуклости, вогнутости и точки

перегиба функции:

; 2)

;

3) y ln 1 x2 ;

4) y

x2 4

2 x

1 2

x 1 2

136

II уровень

2.1. Исследуйте на экстремум функции и инайдите интервалы монотонности:

			x 2									y x5 5x4 5x3 1;
1)	y		x 2				;	2) y x 2 x2	;		3)

		x2
		x2			4x 5
		x						3		2			ex
4)	y			.		5) 1)		y x 1 2x	3	;	6)	y		.
4)	y			.		5) 1)		y x 1 2x	3	;	6)	y		.
		ln x											x

2.2. Найдите наибольшее целое число из промежутка убывания функции:

1)	y sin 2x x,	3	x		;	2) y	1 x x2	, 0 x 1;
		2		2			1 x x2

3)y xx 11, 0 x 4;

2.3.Найдите интервалы выпуклости и вогнутости, а также точки перегиба графика функции:

1) y earctg x ;	2) y arctg	1	;	3) y	2x 1	;
		x			ex

2.4. Определите, каково должно быть соотношение размеров консервной банки цилиндрической формы с заданной поверхностью, чтобы она имела наибольшую вместимость.

2.5.Найдите размеры цилиндра, чтобы при заданном объеме V, он имел наименьшую полную поверхность.

2.6.В равнобедренный треугольник с длинами сторон 15, 15 и 18 см вписан параллелограмм наибольшей площади так, что угол при основании у них общий. Найдите стороны параллелограмма.

2.7.Их трех досок одинаковой ширины сколачивается желоб для

подачи воды. При каком угле наклона боковых стенок к днищу желоба площадь поперечного сечения желоба будет наибольшей.

2.8.На параболе y x2 найти точку N, наименее удаленную от прямой y 2x 4 .

2.9.В полукруг радиуса R вписан прямоугольник с наибольшей площадью. Определить его основание х и высоту у.

2.10. Определите, при каких значениях параметра а кривая

137

yx4 2ax3 6x2 1 выпукла вниз всюду на области определения.

2.11.Найдите положительное число, сумма которого со своей обратной величиной имеет наименьшее значение.

Задания для самостоятельного решения

1. Исследуйте на экстремум функции и найдите интервалы понотонности:

1) y

х2 ; 2) y

x2 2х 2

; 3) y x ln 1 x ; 4)

х 1

2. Найдите наибольше и наименьшее значения функции на отрезке:

1) y

x2 . 2)

y (x 1)e1 x , x 2; 2 . 3) y

x2 , x 1; 2 .

4) y x 33х , x 1; 1 .

3. Найдите интервалы выпуклости, вогнутости и точки перегиба

функции: 1) y	2x 1	; 2) y x ln x 1 ; 3)	y arctgx x ; 4)	y	x	.
	3 x				1 x2

4. Из всех ваз, одинаковой вместимости и имеющих форму усеченного конуса, в котором образующая составляет с основанием угол , найдите ту, у которой полная поверхность минимальна.

5. Найдите число, куб которого превышает утроенный его квадрат, но имеет минимальное значение.

6.7. Асимптоты графика функции. Общее исследование функций

Асимптота графика функции y f x – это прямая линия, к

которой неограниченно приближается график данной функции, когда его точка неограниченно удаляется от начала координат.

Различают горизонтальную, вертикальную и наклонную

асимптоты.
Прямая x a	называется	вертикальной	асимптотой		графика
функции y f x ,	если lim	f x или	lim	f x .
	x a 0		x a 0
В случае вертикальной		асимптоты x a		функция	является
бесконечно большой в точке x a.

138

Прямая y = b называется горизонтальной асимптотой графика

функции y f x , если lim f x b.

Вертикальные асимптоты могут существовать у функций, которые определены не на всей числовой прямой, т. е. имеют разрыв второго рода.

Если областью определения функции является вся числовая прямая, то у функции нет вертикальных асимптот.

Прямая y kx b называется наклонной асимптотой графика

функции y f x ,

Для нахождения формулы:

k lim	f x	,
	x
x

при x , если	lim	f x kx b 0.
	x

коэффициентов k и b применяют следующие

(6.36)	b lim	f x kx .	(6.37)
	x

Если хотя бы один из пределов (6.36), (6.37) равен или не существует, то у функции наклонных асимптот нет.

Если k 0, b 0, то прямая y b является горизонтальной

асимптотой. Заметим, что наклонных асимптот у функции может быть не больше двух, а вертикальных может быть сколько угодно.

Пример 1. Найти асимптоты графика функции:

1) y	x	;	2) y	x 2 3 .

1	x2			x 2 2

Решение. 1) Вертикальных асимптот данная функция не имеет, потому что она определена для любых x ; . Для того чтобы найти горизонтальные асимптоты, надо рассмотреть пределы функции на

бесконечности: lim			x	0.

			1 x2
	x
Получили, что		y 0 – горизонтальная асимптота (ось 0x).
Будем искать		наклонные				асимптоты в виде функции y kx b.
Согласно формулам (6.36) и (6.37), вычисляем:
k lim	x		lim		1		0.

	x 2 x
x 1			x 1		x2

Так как k 0, значит наклонных асимптот у графика нет.

139

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 119 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
31.05.20151.73 Mб20metodichka . физика.pdf
#
31.05.2015597.5 Кб16metodichka по МП пассажиров.doc
#
05.12.20189.82 Mб20Metodichka.doc
#
26.03.20161.61 Mб51MetodichkaC_14ch1.doc
#
26.03.20162.68 Mб20metodichkaFTUG_chast1.pdf
#
26.03.20161.82 Mб6metodichkaFTUG_chast2.pdf
#
10.11.20197.85 Mб10Metodichka_1_kurs.doc
#
26.03.201685.22 Кб12metodichka_magistranty.docx
#
31.05.20151.09 Mб4Metodichka_ME_i_VED.doc
#
20.12.2018310.78 Кб5metodichka_mido-progr.doc
#
11.09.2019825.86 Кб20Metodichka_po_diplomu.doc