
metodichkaFTUG_chast2
.pdf
Приходим к выводу, что x0 4 – точка разрыва II рода (бесконечного
скачка). |
График |
функции |
y |
2 |
|
в окрестности точки x0 4 |
|||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
x 4 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
представлен на рис. 5.1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2) Точкой разрыва данной функции является точка |
x 2. |
Вычислим |
|||||||||||||||||||||||||||
односторонние пределы заданной функции в точке x 2: |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
x 2 0 |
|
|
|
|
|
|
|
|
|
x 2 0 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
2 |
x |
0 |
|
|
|
|
|
|
|
2 |
x |
0 |
|
|
|
|||||||||
lim |
|
1 |
|
|
|
|
1 |
|
|
|
0, lim |
1 |
|
|
|
|
|
1 |
|
|
|
|
1 |
1. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x 2 0 |
|
1 |
|
|
2 |
x |
|
|
x 2 0 |
|
1 |
|
|
2 |
x |
|
|
1 0 |
|
||||||||||
|
|
|
|
|
|
1 32 x |
|
|
|
|
|||||||||||||||||||
1 32 x |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
32 x |
|
|
|
|
|
|
|
|
32 x 0 |
|
|
|
|||||||||||
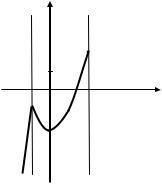
у
0
4 |
х |
Рис. 5.1
Получили, что оба односторонних предела существуют (и конечны), но не равны между собой. Поэтому x 2 – точка разрыва I рода (скачок) – рис. 5.2. Заметим, что скачок равен:
lim |
f x |
lim f x 0 1 1. |
|
x 2 0 |
|
x 2 0 |
|
|
|
у |
|
|
|
|
1 |
|
|
– 2 |
х |
70
|
Рис. 5.2 |
|
|
||
|
x3 |
, |
если |
x 1, |
|
Пример 3. Дана функция |
|
2 |
2, если |
1 x 2, |
|
f (x) x |
|
||||
|
3, |
|
если |
x 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Исследовать ее на непрерывность и разрыв. Построить график. Решение. На промежутках ; 1 , 1; 2 , 2; функция задана
аналитическими выражениями элементарных функций, которые определены и, следовательно, непрерывны на каждом промежутке. Поэтому точками, «подозрительными на разрыв», являются точки x 1 и x 2.
Вычислим односторонние пределы функции в точке x 1. |
|
|||
Так как функция |
f x x3 |
при x 1, то lim f |
x lim |
x3 1. |
|
|
x 1 0 |
x 1 0 |
|
|
|
|
|
|
Так как функция |
f x x2 |
2 при 1 x 2, то |
|
|
lim f x lim x2 2 1. |
|
|
||
x 1 0 |
|
|
|
|
Вычислим значение функции в точке x 1: f 1 1 3 |
1. |
|||
Таким образом, условия непрерывности функции в точке –1 выполнены. Поэтому в точке x 1 разрыва нет.
Вычислим односторонние пределы функции в точке x 2.
Так как функция |
f x x2 2 при 1 x 2, то |
|
|
lim f x |
lim |
x2 2 2. |
|
x 2 0 |
x 2 0 |
|
|
|
|
|
|
Так как функция |
f x 3 при x 2, то lim f x |
lim 3 3. |
|
|
|
x 2 0 |
x 2 0 |
|
|
|
|
Получили, |
что x 2 – точка разрыва I рода (скачок). Значит, функция |
||
непрерывна всюду на числовой прямой кроме точки |
x 2 (рис. 5.3), в |
||
которой она имеет скачок, равный 1. |
|
||
у
3 

1
– 1 |
0 |
2 |
х |
71

Рис. 5.3
Пример 4. Используя свойства непрерывных функций, доказать, что
уравнение 3x3 x2 12x 4 имеет |
хотя |
бы один корень в промежутке |
||
1; 0 . |
|
|
|
|
Решение. |
Рассмотрим |
функцию |
f x 3x3 x2 12x 4. Она |
|
непрерывна |
на отрезке |
1; 0 |
как |
сумма элементарных функций. |
Вычислим значения функции на концах отрезка: f 1 3 1 12 4 6 0, f 0 4 0.
Получаем, что функция на концах отрезка принимает значения разных
знаков, потому существует |
точка x 1;0 , в |
которой |
функция |
|
обращается в нуль, т. е. |
3 x x 12 x 4 0. |
|
|
|
Другими словами, |
точка |
х будет являться |
корнем |
уравнения |
3x x 12x 4 0. |
|
|
|
|
Задания для решения в аудитории
I уровень
1.1. Вычислите односторонние пределы функции:
|
|
x 3 |
|
|
|
|
|
3 |
|
|
|
|
|||
|
|
|
б) lim |
1 |
|
; |
x 1 x 4 |
|
|||||||
а) |
lim |
|
|
|
; |
|
|
в) lim |
|
|
|
|
; |
||
|
x 1 0 |
x 1 |
|
x 3 0 |
x |
3 3 |
|
x 0 |
|
x2 |
|
||||
г) |
lim |
|
x2 |
x 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
|
|
|
|
|
|
|
|
|
|||
|
x 2 0 |
|
|
|
|
|
|
|
|
|
|
||||
1.2. Приведите пример непрерывной функции: 1) на всей числовой прямой; 2) при всех значениях х, кроме x 1; 3) при всех
значениях х, кроме x 0, x 5; 4) на луче ; 1 ; 5) на интервале
(0; 2); 6) на отрезке [– 1; 1].
1.3. Исследуйте функцию y = f(x) на непрерывность. Найдите
72
точки разрыва и классифицируйте их. В случае устранимого разрыва доопределите функцию до непрерывной.
1) |
y |
1 |
; |
2) |
y |
|
x 1 |
|
; |
3) |
y |
1 |
|
; |
4) y |
x2 4 |
; |
|
||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
2x 1 |
|
x 1 |
|
4 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
x 2 |
||||||
5) |
y |
sin( x 2) |
; 6) |
y |
|
1 |
|
|
7) |
y |
3x 2 |
; |
8) y |
|
x 2 |
|||||||
|
|
|
|
|
; |
|
|
|
. |
|||||||||||||
|
x 2 |
|
3x 1 |
|
x 2 |
x 1 2x |
||||||||||||||||
1.4. Исследуйте функцию на непрерывность, постройте ее график. Вычислите скачок функции в соответствующей точке разрыва:
|
|
|
|
|
|
|
|
|
||
|
x 4, если |
|
x 2, |
|
|
|||||
|
|
|
|
|
|
|
|
|
||
1) |
|
если |
2 x |
, |
||||||
f (x) 2, |
2 |
|||||||||
|
|
|
|
|
|
|
|
|||
|
|
если |
x |
. |
|
|
||||
|
sin x, |
|
|
|
||||||
|
|
|
|
|
2 |
|
|
|
||
|
1 |
, если |
x 1, |
|
|
|||||
|
|
|
|
|
|
|||||
|
x 1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
||
3) |
f (x) 2, если |
1 x 3, |
|
|
||||||
|
x 1, |
если |
x 3. |
|
|
|||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
2)f (x)
4)f (x)
x 4, если x 1,
x2 2, если 1 x 1,2x, eсли x 1;
x3 , если x 1,
2 x, если x 1.
II уровень
2.1. С помощью односторонних пределов определите, имеет ли функция предел в точке. В случае существования вычислите его:
|
|
|
|
|
|
|
|
|
|
|
|
x2 1 |
|
|
|
|
|
|
1) |
lim |
2 x |
; |
2) lim |
|
; |
3) lim |
|
3x |
|
; |
|||||||
|
|
|
|
x2 |
4x 3 |
|
x |
|
||||||||||
|
x 4 16 x2 |
|
|
|
x 1 |
|
x 2 |
2 |
|
|||||||||
|
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|||
4) |
lim |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
||
|
2 x |
|
8 x |
3 |
|
|
|
|
|
|
|
|
||||||
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2.2. Вычислите односторонние пределы функции в точке:
|
|
1 |
|
|
|
|
|
1 |
|
||
|
|
|
|
2) lim arctg3x; |
|
|
|
||||
1) lim |
|
|
; |
3) lim ln e x ; |
|||||||
|
|
|
|
||||||||
|
|
1 |
|
||||||||
x 2 0 |
|
|
x |
|
0 |
x 0 |
|||||
3x 2 |
|
|
|||||||||
1 |
|
|
6 |
|
|
|
|||||
73

|
4) |
lim arcsinln 2 x . |
|
|
|
|
|
|
|
|
x 2 0 |
|
|
|
|
|
|
|
|
|
2.3. |
Вычислите |
односторонние |
пределы |
функции y f x в |
||||
точке x0 : |
|
|
|
|
|
|
|
||
|
2, если x 1, |
|
|
x |
|
x 3, |
|
||
|
|
arctg |
|
|
, если |
|
|||
|
|
|
|
|
|||||
1) |
y |
x0 1. 2) |
y |
3 |
|
|
x0 |
3. |
|
|
ln x, если x |
1, |
(x 3)2 |
, если |
x 3, |
|
|||
|
|
|
|
|
|
|
|
|
|
2.4. Пользуясь определениями непрерывности функции в точке, докажите, что функция f(x) непрерывна всюду на числовой прямой:
1) f (x) x3 ; |
2) f (x) x2 3; |
3) |
f (x) |
1 |
; |
||
|
|
||||||
x2 |
1 |
||||||
|
|
|
|
|
|||
4)f (x) 3 x 1.
x 1.
2.5.Определите точки разрыва функции и установите их тип:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1) |
y |
|
|
1 |
|
|
; |
2) |
y |
1 |
; |
|
|
3) |
y |
2 x2 |
1 |
; |
||||||
|
|
1 |
x |
|
|
1 |
|
|
|
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
|
|
|
|
|
|
|
1 |
|
|
arctg |
|
|
|
|
|
|
2 x |
|
|
1 |
|
|||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4) |
y |
|
|
x |
|
; |
5) |
y x 2 arctg |
1 |
; |
6) |
y |
5x 3 |
1 |
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
sin x |
|
|
|
|
|
x |
|
|
|
x 3 |
|
|||||||||||
2.6. Исследуйте функцию на непрерывность, постройте ее график. Найдите точки разрыва и классифицируйте их. В случае устранимого разрыва доопределите функцию до непрерывной:
|
|
1 |
|
|
|
|
|
|
|
|
x 2 |
|
|
|
||||
|
|
, если |
x 2, |
|
x |
|
|
|
|
, |
если x 2, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x 1 |
|
x 2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1) f (x) |
1, |
|
|
|
если |
2 x 4, 2) |
f (x) |
2 , |
|
если 2 x 0, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
4x 2, |
если x 4; |
|
|
1 |
|
|
|
|
|
|||||||
|
x |
|
|
|
|
|
, |
|
|
если x 0; |
||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
x2 |
4 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.7. Задана функция f(x). Найдите все значения параметров, при которых функция непрерывна:
74
ax 1, |
если x 2, |
|
0, |
если x 0, |
|
|
|
если 0 x 1, |
|||
|
|
|
|
ax, |
|
1) f (x) sin |
, |
если x 2; |
2) |
f (x) x2 |
bx 2, если 1 x 3, |
|
x |
|
|
|
|
|
|
|
b x, если x 3. |
||
|
|
|
|
||
|
|
|
|
|
|
2.8. Докажите, что уравнение имеет хотя бы один корень на указанном промежутке:
1)5x(x2 2) 8 18x2 , если x 0; 1 .
2)x3 19x 30, если x 3; 6 .
3)2x3 5x2 8x 20, если x 3; 0 .
Задания для самостоятельного решения
1. Вычислите односторонние пределы функции:
|
2x 1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
x 4 |
|
||||||
1) lim |
; 1.2. |
lim |
|
; 1.3) |
lim 1 |
2x 1 ; |
||||||
x 2 |
2 |
|
|
|
||||||||
x 2 0 |
|
x 0 |
x |
|
|
|
|
|||||
|
|
|
|
|
|
x 1 0 |
|
|
|
|||
|
x 1, если |
x 0, |
|
|
4) |
y |
x 0, |
x0 |
0. |
|
sin x, если |
|
|
2. Исследуйте функцию на непрерывность, постройте ее график. Найдите точки разрыва и классифицируйте их. В случае устранимого разрыва доопределите функцию до непрерывной:
|
|
x3 |
1 |
|
|
|
|
x 2 |
|
|
|
|
2 |
|
|
2x 4 |
|
||
1) |
f (x) |
; |
|
|
2) y |
; |
3) f (x) 6 |
4 x ; 4) |
f (x) |
; |
|||||||||
x |
1 |
|
|
|
5x |
3x 9 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, если x 0, |
|
|
|
1 x, если |
x 0, |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
5) |
f (x) 1 x, |
если 0 x 3, |
6) |
f (x) |
|
|
, |
если |
0 x 2, |
|
|||||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
2 |
, если x 3; |
|
x |
|
|
|
|
|
||||
|
|
x 3 |
|
|
x |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
если |
x 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
75

6. Дифференциальное исчисление функции одной переменной
6.1. Производная функции
Определение производной. Пусть функция |
y f (x) |
определена в некоторой окрестности фиксированной точки x0 и пусть х – произвольная точка этой окрестности. Тогда x x0 x
приращение аргумента (положительное или отрицательное) такое, что x x принадлежит окрестности этой точки, и приращение
функции |
в |
точке |
x0 |
выразится |
формулой |
f (x0 ) f (x0 x) f (x0 ).
Производной функции y f (x) в точке x0 называется предел
отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. Обозначение производной
в точке x0 |
: y '(x0 ), |
f ' x0 |
, |
df x0 |
|
, |
dy |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||||||
dx |
dx |
x x0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
Следовательно, по определению |
|
|
|
|
|
|
|
|
||||||
f ' x |
lim f (x0 ) lim |
f (x0 |
x) f (x0 ) |
. |
(6.1) |
|||||||||
|
|
|||||||||||||
0 |
x 0 |
x |
x 0 |
|
x |
|
|
|
||||||
|
|
|
|
|
||||||||||
Таким |
образом, производная функции |
в точке |
x x0 (если |
|||||||||||
существует) – есть определенное число. Если же производная существует в произвольной точке х, то она является функцией от х и обозначается:
y ', f '(x), dy , df (x) . dx dx
Операция нахождения производной от функции f(x) называется
дифференцированием этой функции. Дифференцируемой
называется функция, которая имеет производную.
Основные правила дифференцирования
Пусть с – постоянная, u(x) и v(x) - дифференцируемые функции. Тогда
76
1. c ' 0. |
2. (u v) ' u ' v '. |
|
3. (uv) ' u 'v uv '. |
||||||||
4. (c u) ' cu '. |
u ' |
|
u 'v uv ' |
v 0 . |
|||||||
5. |
|
|
|
|
|
|
|
||||
|
|
v |
2 |
|
|
||||||
|
|
v |
|
|
|
|
|
|
|||
Если y f (u) , |
u u(x) , где u(x) |
– дифференцируема в точке |
|||||||||
x, а функция |
f (u) |
дифференцируема |
|
в соответствующей точке |
|||||||
u u(x) , то |
сложная функция |
y f (u(x)) дифференцируема в |
|||||||||
точке x и ее производная y ' |
f ' (u)u '(x). |
|
|||||||||
|
|
|
|
|
|
u |
|
|
|
|
|
Таблица производных основных элементарных функций
1. un ' n un 1 u ', n R.
2. au ' au ln a u ', a 0, a 1.
3. eu ' eu u '.
4. |
loga u ' |
|
u ' |
, |
a 0, |
a 1. |
|||
|
|
||||||||
u ln a |
|||||||||
|
|
|
|
|
|
|
|||
5. |
ln u ' |
u ' |
. |
|
|
|
|
||
|
|
|
|
|
|||||
|
|
u |
|
|
|
|
|||
6. |
sin u ' cosu u '. |
|
|
||||||
7. |
cosu ' sin u u '. |
|
|||||||
8. tgu ' |
|
u ' |
|
|
. |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
cos2 u |
|
|
|
|
|
|
|
|
|
||||||||||
9. ctgu ' |
u ' |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||||
sin2 u |
|
|
|
|
|
|
|
||||||||||||
10. |
arc sin u ' |
|
|
|
|
|
|
u ' |
|
|
. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
1 u2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
11. |
arccosu ' |
|
|
|
|
u ' |
|
|
|
|
. |
||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 u2 |
||||||||
12. |
arctgu ' |
|
|
u ' |
. |
|
|
|
|
|
|
||||||||
|
u2 |
|
|
|
|
|
|||||||||||||
|
1 |
|
|
|
|
|
|
|
|||||||||||
13. |
arcctgu ' |
|
u ' |
|
. |
|
|
||||||||||||
|
u2 |
|
|
||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||
Пример 1. Найти производную функции |
y x |
в точке x0 , |
пользуясь |
||
определением, если: 1) |
y x 2x2 3x 4, x |
2; 2) |
y(x) sin x, |
x . |
|
|
0 |
|
|
0 |
4 |
|
|
|
|
|
|
Решение. 1) Используем определение производной в виде формулы
(6.1):
77
y |
(x ) lim |
|
f (x0 |
x) f (x0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
0 |
|
x |
0 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
lim |
|
2(x x)2 |
3(x x) 4 2x2 3x 4 |
|
|
|
|
|
|
|||||||||||||||
0 |
|
|
|
0 |
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x 0 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
lim |
|
2x2 |
4x x 2 x2 3x 3 x 4 2x2 3x 4 |
|
|
|
||||||||||||||||||
0 |
|
|
|
0 |
|
|
0 |
|
|
|
|
|
0 |
|
|
0 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x 0 |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
4x x 2 x2 3 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
lim |
0 |
|
|
|
|
|
|
lim(4x0 2 x 3) 4x0 |
3. |
|
|
|||||||||||||
|
|
|
|
|
x |
|
|
|
|
||||||||||||||||
|
x 0 |
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
||||||
Поскольку по условию x0 2, |
|
то y 2 4 2 3 5. |
|
|
|
||||||||||||||||||||
2) По формуле (6.1) получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
y (x ) lim |
|
f (x0 |
x) f (x0 ) |
lim |
sin(x0 x) sin x0 |
. |
|||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
0 |
|
x 0 |
|
x |
|
|
|
|
x 0 |
|
|
x |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Далее, применив тригонометрическую формулу |
|
|
|
|
|
||||||||||||||||||||
sin( ) sin cos cos sin , |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
lim |
sin x0 cos x cos x0 sin x sin x0 |
|
lim |
|
sin x0 cos x |
|
|||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|||||||||||||||||
x 0 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
x 0 |
|
|
|
|
|||||||
lim |
cos x0 sin x |
lim |
sin x0 |
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x 0 |
|
|
|
x 0 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Так как при |
x 0 имеем |
|
cos x cos0 1 |
|
и, |
применив формулу |
|||||||||||||||||||
первого замечательного предела, получаем: |
|
|
|
|
|
|
|
|
|
||||||||||||||||
lim |
sin x0 |
lim cos x |
lim |
sin x0 |
|
|
|
||||
x 0 |
x |
x 0 |
0 |
x 0 x |
|
|
|||||
Поскольку по условию x0 4 , то
lim cos x0 cos x0.
x 0
|
|
|
|
|
|
2 |
|
|
y |
|
|
cos |
|
|
|
|
. |
|
|
|
|
|||||
|
4 |
|
|
4 |
|
2 |
|
|
|
Пример 3. Найти производную функции: |
|
|
|
|
|||||||
|
|
log2 |
x |
|
|
|
|
|
|
x3 |
||
1) |
y 4cos x |
arctgx; |
2) y 2 xtgx 5; |
3) |
y |
|||||||
|
|
|
. |
|||||||||
3 |
|
x5 1 |
||||||||||
Решение. 1) Используем основные правила дифференцирования (вторую и четвертую формулы) и таблицу производных, получаем:
78

|
|
log2 x |
|
|
log2 |
|
|
|
|
|
|
|
x |
|
|||||||
y |
4 cos x |
|
arctgx |
4 cos x |
|
|
|
|
arctgx |
|
3 |
3 |
|
||||||||
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
1 |
|
1 |
|
|
4 cos x |
|
|
log2 x |
arctgx |
4sin x |
|
|
|
. |
|
3 |
3x ln 2 |
1 x2 |
||||||||
|
|
|
|
|
|
|
2) Используем основные правила дифференцирования (1-4 формулы) и соответствующие формулы таблицы производных:
y |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
tgx |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
2 xtgx |
5 |
|
|
xtgx 0 |
|
x |
x tgx |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
tgx |
|
|
2 |
|
|
x |
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
tgx x |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||
|
2 x |
cos |
|
|
|
x |
cos |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||||||||||
3) Используем основные правила дифференцирования (пятую формулу) и первую формулу таблицы производных:
|
|
|
x3 |
|
x |
3 |
5 |
1 x |
3 |
x |
5 |
|
|
|
2 |
x |
5 |
1 |
x |
3 |
5x |
4 |
0 |
|
||||||||
|
|
|
|
x |
|
|
|
1 |
|
3x |
|
|
|
|
|
|||||||||||||||||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||
|
|
|
1 |
|
|
|
|
|
|
|
x5 |
1 |
|
|
|
|
|
|
|
|
|
x5 |
1 |
|
|
|
|
|||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
3x7 |
3x2 5x7 |
|
2x7 3x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
x5 1 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x5 1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Пример 4. Вычислить производную функции, используя правила |
|||||||||||||||||||||||||||||||
дифференцирования и таблицу производных: 1) |
y log2 (x5 2x )sin x ; |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2) |
|
y ln |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
thx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. 1) Преобразуем функцию, пользуясь свойствами логарифма: |
|||||||||||||||||||||||||||||||
|
y log2 (x5 2x )sin x |
sin x log2 (x5 2x ) sin x(log2 x5 |
log2 |
2x ) |
|
|||||||||||||||||||||||||||
|
sin x(5log2 |
x x). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Полученное выражение дифференцируем используя основные правила дифференцирования (вторую, третью и четвертую формулы) и формулам таблицы производных:
y ' (sin x(5log2 x x)) ' (sin x) ' (5log2 x x) sin x (log2 x x) '
|
|
5 |
|
cos x(5log2 |
x x) sin x |
|
1 . |
|
|||
|
x ln 2 |
|
|
79
