
metodichkaFTUG_chast2
.pdf
1. Если материальная точка M движется неравномерно по пути, заданному функцией y S t , то мгновенная скорость движения в момент времени t0 есть производная от пути S по времени t:
(6.23)
2. Если функцией y v t описывается процесс изменения
скорости неравномерного движения в зависимости от времени, то мгновенное ускорение материальной точки в момент времени t0 есть производная от скорости v по времени t:
a t0 v t0 . |
(6.24) |
Экономические приложения производной
1. Если предприятие выпускает однородную продукцию и издержки производства у являются функцией от количества выпускаемой продукции х, т.е. y f x . Тогда средние издержки
производства |
на единицу выпуска продукции |
будут |
y |
, а |
|
|
|||||
|
|
|
|
x |
|
мгновенные |
(предельные) |
издержки |
производства: |
||
y f x lim |
y . |
|
|
|
|
x 0 |
x |
|
|
|
|
2. Если |
функция u u t |
выражает объем |
произведенной |
||
продукции за время t. Тогда производная объема произведенной продукции по времени t - есть производительность труда u t0 в
момент времени t0 .
3.Эластичность функции Ex y это предел отношения
относительного приращения функции к относительному приращению аргумента, когда приращение аргумента стремится к нулю.
|
|
|
y |
|
|
y |
|
x |
|
|
|
x |
|
y |
|
|
Из определения |
E |
|
lim |
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
x |
|
x 0 |
y |
|
x |
|
|
x 0 y |
|
x |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ex y xy y
x |
lim |
y |
|
x |
y , |
|
x |
|
|||
y x 0 |
|
y |
|
||
(6.25)
Эластичность – это мера реагирования одной переменной
110
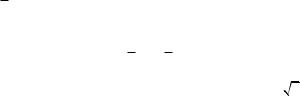
величины на изменение другой. Она приближенно показывает, на сколько процентов изменится функция при изменении независимой переменной х на один процент.
Эластичность функции применяется при анализе спроса и предложения от цены. Если эластичность функции спроса больше единицы, то спрос – эластичный, если равна единице – нейтральный, а если меньше единицы – не эластичный относительно цены.
Пример 1. Написать уравнение касательной и нормали, проведенной к
графику функции y |
4x 3 |
в точке с абсциссой x = 2. |
||
3 2x |
|
|||
|
|
|||
Решение. Для нахождения уравнения касательной воспользуемся формулой (6.21). Сначала найдем ординату точки касания f (x0 ). Для этого
значение x 2 подставим в уравнение функции: |
|
|||||||||||||
f 2 |
4 2 3 |
5. |
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||||
|
|
|
3 2 2 |
|
|
|
|
|
|
|
||||
Для нахождения |
|
углового |
коэффициента найдем производную y ', |
|||||||||||
используя формулу дифференцирования дроби: |
|
|||||||||||||
y 4x 3 ' 3 2x 4x 3 3 2x ' |
4 3 2x 2 4x 3 |
|
||||||||||||
3 2x 2 |
||||||||||||||
|
|
|
|
|
|
|
3 2x 2 |
|
|
|||||
|
|
12 8x 8x 6 |
|
|
|
6 |
. |
|
|
|||||
|
|
|
3 |
2x 2 |
|
|
||||||||
|
|
3 2x 2 |
|
|
|
|
|
|||||||
Найдем значение производной при x 2 : |
|
|||||||||||||
|
|
|
6 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y |
2 3 2 2 2 |
6. |
|
|
|
|||||||||
|
|
|
|
|||||||||||
Подставив найденные значения в формулу (6.21), получаем уравнение касательной:
y 6 x 2 5, т. е. y 6x 17.
Чтобы написать уравнение нормали, воспользуемся формулой (6.22):
y 16 (x 2) 5.
Получим, что уравнение нормали, проведенной к заданной кривой в заданной точке, имеет вид y 16 x 4 23 .
Пример 2. Определить, в какой точке кривой y 33 x касательная
x касательная
111
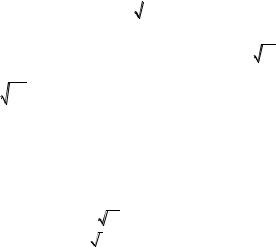
наклонена к оси абсцисс под углом 45 .
Решение. Так как тангенс угла наклона касательной к оси абсцисс равен значению производной в точке касания, найдем производную функции:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
2 |
|
|
1 |
|
|
|
||
y |
3x3 |
3 |
3 |
|
|
|
|
|
||||||
|
x |
|
|
|
|
|
. |
|||||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
3 |
|
|
3 |
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По условию y (x0 ) tg45 . Следовательно, |
1 |
|
1. |
|||||||
|
|
|
||||||||
|
|
|
||||||||
3 x2 |
||||||||||
|
|
|
|
|
|
|
|
|||
Отсюда: |
|
|
|
|
|
|
|
|||
|
|
|
x 2 |
|
|
|
|
|
|
|
3 x 2 1, |
1, |
x 1. |
|
|
|
|
||||
0 |
|
0 |
|
0 |
|
|
|
|
||
Получили два значения абсциссы точки касания:
x01 1, x02 1,
т. е. существуют две точки касания, в которых касательная образует угол 45 с осью Ох.
Найдем соответствующие ординаты точек касания, подставляя значения x01, x02 в формулу функции:
y(x ) y( 1) 33 |
|
1 |
3; |
|
|
|
|
01 |
|
|
|
|
|
|
|
|
|
|
|
||||
y(x ) y(1) 33 |
1 |
3. |
|
|
|
||
02 |
|
|
|
|
|
|
|
Приходим к ответу: в точках |
M01( 1; 3) |
и M02 (1; 3) |
касательная к |
||||
заданной кривой образует с осью Ох угол 45 . |
|
|
|||||
Пример 3. Найти острый |
угол между |
параболами |
y 3x2 и |
||||
y x2 4 в точке их пересечения, имеющей отрицательную абсциссу.
Решение. Угол между двумя кривыми в точке их пересечения – это угол между касательными к этим кривым, проведенными в точке их пересечения. Тангенс этого угла вычислим по формуле
|
|
tg |
k2 k1 |
|
|
, |
(6.26) |
|
|
1 k k |
2 |
|
|||
|
|
|
1 |
|
|
|
|
где k1 и |
|
k2 – угловые коэффициенты касательных, |
проведенных к |
||||
параболам в заданной точке. |
|
|
|
|
|
||
Найдем точку пересечения этих парабол. Для этого решим систему: |
|||||||
|
2 |
|
|
|
|
|
|
y 3x |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
y x2 4. |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Отсюда x 1. Условию задачи удовлетворяет точка |
x0 1. Найдем |
||||||
112

коэффициент k1:
y 3x2 , y x 6x, y x0 y 1 k1 6 1 6.
Аналогично найдем k2:
y x2 4, y x 2x, y x0 y 1 k2 2.
Воспользуемся формулой (6.26) и получим:
tg |
|
2 6 |
|
|
|
8 |
|
|
8 |
, |
||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||
|
1 2 6 |
11 |
11 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
откуда arctg 118 .
Пример 4. Тело движется прямолинейно по закону
S t 16 t3 3t2 5.
Найти скорость движения тела в тот момент, когда ускорение равно нулю.
Решение. Согласно формуле (6.23), скорость есть производная функции S(t), а, согласно формуле (6.24), ускорение а(t) есть производная скорости v(t).
Последовательно вычислим производные:
|
|
|
3 |
|
3 |
|
1 |
|
3 |
|
v t S |
t 6 t |
|
6t 2 t |
|
6t; |
|||||
|
|
|
||||||||
|
|
|
3 |
|
2 |
|
|
|
|
|
a t v |
t 2 t |
|
6. |
|
|
|||||
|
|
|
|
|||||||
Найдем момент времени, когда ускорение равно нулю:
32 t 2 6 0; 3t 2 12; t 2.
Вычислим скорость движения тела в момент времени t0 2 :
v t0 v 2 12 23 2 6 8.
Пример 5. Зависимость между себестоимостью единицы продукции у (в тыс. руб.) и выпуском продукции х (в млрд. руб.) выражается функцией: y 0,5x 80 . Найти эластичность себестоимости при выпуске продукции
равном 60 млрд. руб.
Решение. Согласно формуле (6.25), эластичность функции
себестоимости
113
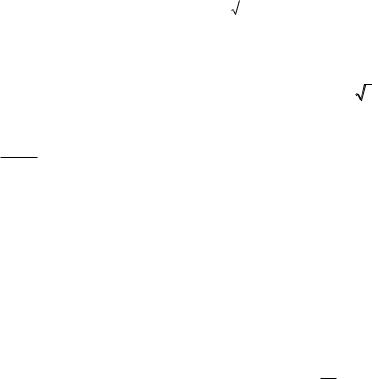
|
|
|
x |
|
|
|
|
|
|
0,5x |
|
x |
|
||||
|
|
|
|
|
|
|
|
|
|
||||||||
Ex y |
|
|
|
|
y |
|
y |
0,5x 80 |
0,5 |
|
|
|
|
|
, при |
||
0,5x 80 |
0,5x 80 |
x 160 |
|||||||||||||||
|
|
60 |
|
|
|
|
|
|
|
||||||||
x0 |
60 E60 |
y |
|
|
|
0,6 . |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
160 |
|
|
|
|
|
|
|
|||||||||
|
|
|
60 |
|
|
|
|
|
|
|
|
|
|||||
Это означает, что при выпуске продукции равном 60 млрд. руб. увеличение его на 1% приведет к снижению себестоимости на 0,6%.
Задания для решения в аудитории
I уровень
1.1. Напишите уравнения касательной и нормали к кривой y f (x) в точке х0:
|
y x3 2x 2, x0 1. |
|
|
|
|
|
|
|
|
|
|
|
|||
1) |
|
2) |
y |
x 4, |
x0 8. |
|
|
|
|
||||||
3) |
y cos x |
x2 |
, |
x |
; |
4) |
y 2x |
3 |
x2 3, |
x |
1. |
||||
|
|
||||||||||||||
|
|
|
|
0 |
|
|
|
|
ln 2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1.2. Найдите угол, |
под которым график функции |
y |
1 |
sin 3x |
||||||||||
|
|
|
|||||||||||||
|
3 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
пересекает ось абсцисс в начале координат.
1.3. Определите, в какой точке касательная к графику функции
y 2x 2 образует с осью абсцисс угол 45 . x 2
1.4. Зависимость между издержками производства у и объемом выпускаемой продукции х на предприятии выражается функцией
y 50x 0,05x3 . Определить средние и предельные издержки при
объеме продукции 10 единиц.
1.5. Производительность труда бригады может быть описано уравнением y 2,5t 2 15t 100 , где 0 t 8 - рабочее время в часах.
Вычислить скорость изменения производительности труда при t1 2, t2 7 часов.
1.6. Зависимость между количеством выпускаемых деталей в партии х (тыс. ед.) и затратами на их изготовление у (тыс. ед.) для
предприятий отрасли выражается уравнением y 27x 6 . Найти
эластичность затрат для предприятий, выпускающих по 10 тыс. деталей в партии.
114

II уровень
2.1. Составьте уравнение касательной к графику функции y 13 (x3 1) в точке его пересечения с осью абсцисс.
2.2. |
Найдите |
площадь |
треугольника, |
ограниченного |
осями |
|||
координат и касательной к графику функции y |
|
x |
|
|||||
|
|
в точке, |
||||||
|
2x 1 |
|||||||
ордината которой равна 1. |
|
|
|
|
|
|
||
2.3. |
Найдите |
точку на |
кривой y 5x2 |
4x 1 , касательная в |
||||
которой перпендикулярна к прямой x 6y 15 0 . |
|
|
|
|
||||
2.4. |
Касательная к параболе y x2 mx 6 |
проходит |
через |
|||||
начало координат. Найдите значение параметра m, при котором
абсцисса точки касания положительна, а ордината равна 8. |
|
||||||||
2.5. Определите, |
при |
каких значениях параметра m прямая |
|||||||
x y 1 0 |
является |
касательной |
к |
графику |
функции |
||||
y x2 mx m. |
|
|
|
|
|
|
|
||
2.6. Записать уравнение касательной и нормали в точке M0 2; 2 |
|||||||||
к кривой x |
1 t |
, y |
2 |
|
1 |
. |
|
|
|
|
|
|
|
|
|
||||
|
t3 |
2t 2 |
2t |
|
|
|
|||
2.7. Запишите уравнения касательных |
и нормалей |
к кривой |
|||||||
x2 y2 4x 2 y 3 0 в точках пересечения ее с осью Ох.
2.8. Прямая пересекает параболу y x2 2x 4 в двух точках A( 2; 4) и B(1; 5). Напишите уравнение касательной к параболе,
параллельной этой секущей. Найдите угол, под которым нормаль, проведенная в точку касания, пересекает ось абсцисс.
2.9. Найдите угол между кривыми y 
 2 sin x, y
2 sin x, y 
 2 cos x .
2 cos x .
2.10. В какой точке параболы y2 8x ордината возрастает в 2
раза быстрее.
2.11. Тело брошено вертикально вверх. Закон движения тела s t 4 8t 5t 2 . Определите: 1) скорость в момент времени t = 0; 2)
скорость в момент времени соприкосновения с землей; 3) наибольшую высоту подъема; 4) ускорение этого тела в момент
115

времени t = 1 c.
2.12. Движения двух материальных точек по одной прямой заданы уравнениями s(t) 24x2 24x и s(t) 4x2 7. Найдите
скорости движения точек в те моменты, когда пройденные ими расстояния равны.
2.13. Зависимость между себестоимостью готовой продукции предприятия у (млн. руб.) и объемом выпускаемых изделий х (тыс.
шт.) выражается уравнением y 
 x 4 2 . Найдите эластичность
x 4 2 . Найдите эластичность
себестоимости продукции предприятия, выпускающего 12 тыс. шт. изделий. Какие рекомендации можно дать руководителям предприятия об изменении величины объема выпускаемой продукции?
2.14. Заданы функции спроса q и предложения s от цены x: q 10 x, s 3x 6 . Найдите: 1) равновесную цену; 2) эластичность
спроса и предложения для равновесной цены; 3) изменение дохода при изменении равновесной цены на 5%.
|
|
|
Задания для самостоятельного решения |
|
|||||
|
1. |
Составьте уравнение касательной |
к |
графику |
функции |
||||
y |
1 |
(x3 1) в точке его пересечения с осью абсцисс. |
|
||||||
|
|
||||||||
|
3 |
|
|
|
|
|
|
|
|
|
2. |
Тело движется по закону s(t) 2t3 3t 4. |
Найдите скорость |
||||||
и ускорение тела в момент времени t 2. |
|
|
|
||||||
|
3. |
Найдите точку на кривой |
y |
x4 |
7 , |
касательная в которой |
|||
|
|
||||||||
|
|
|
|
4 |
|
|
|
|
|
параллельна прямой y 8x 4 , |
и напишите уравнений |
нормали, |
|||||||
проведенной в этой точке. |
|
|
|
|
|
|
|||
|
4. |
Снаряд массой m выпущен вертикально вверх из зенитного |
|||||||
орудия с начальной скоростью 50 м/с. Найдите кинетическую
энергию снаряда |
в момент времени t0 3. |
Определите, |
на какой |
|
высоте кинетическая энергия равна нулю. |
|
|
|
|
5. Найдите |
уравнение касательной |
и |
нормали |
к кривой |
4x3 3xy 6x2 5xy 3y2 9x 14 0 в точке (-2; 3). |
|
|||
6. Найдите угол между кривой y x x3 |
и прямой y 5x . |
|||
116
7. По оси Ох движутся две материальные точки, законы
движения которых y |
4t 3 |
7t 16 и |
y t 3 2t 2 5t 8 . В какой |
|
3 |
||||
|
|
|
момент времени их скорости окажутся равными и чему она равна? В какой момент времени скорость движения первой точки будет равна
9 м/с?
8. Себестоимость продукции у связана с объемом выпускаемой продукции х уравнением: y 6ln 1 3x . Определите среднюю и
предельную себестоимость выпускаемой продукции при объеме, равном 10 единиц.
9. Найдите эластичность функции спроса q при заданной
стоимости р: а) q 10p 50, |
p 3; |
б) 5q 3p 70, |
p 10; |
||
в) p2 p 4q 26, p |
2; p |
2 |
4. |
|
|
1 |
|
|
|
|
|
6.5. Теоремы о среднем. Правило Лопиталя. Формула Тейлора
Точка х0 называется точкой локального максимума (минимума) функции f(x), если существует некоторая окрестность точки x0 такая, что для всех x из этой окрестности выполняется неравенство f (x) f (x0 ) f (x) f (x0 ) .
Значение f (x0 ) называется локальным максимумом
(минимумом) функции.
Точки максимума или минимума функции называются точками экстремума (локального). Максимум и минимум называются
экстремумом функции.
Теорема 1 (теорема Ферма). Если функция f(x)
дифференцируема в точке |
x0 и в этой точке достигает локального |
|
экстремума, то производная в этой точке равна нулю. |
||
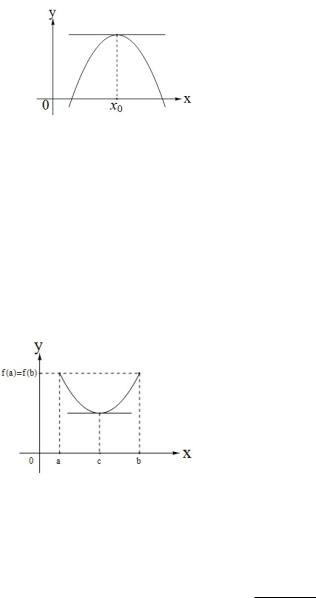
Геометрический смысл теоремы Ферма. |
||
Если |
f x0 0 , то |
в точке локального экстремума |
x0 , y0 касательная к кривой параллельна оси Ох.
117
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.1 |
|
|
|
|
Теорема |
2 |
|
(теорема |
Ролля). |
|
Если |
функция |
|
y f x удовлетворяет трем условиям: 1) функция f(x) непрерывна |
||||||||
на отрезке |
a;b ; 2) |
функция f(x) дифференцируема на интервале |
||||||
a;b ; 3) |
значения |
|
функции на |
концах |
отрезка |
совпадают |
||
f a f b , |
|
то внутри этого интервала найдется по крайней мере |
||||||
одна точка x c , в которой производная равна нулю f c 0 .
Геометрический смысл теоремы Ролля.
Если выполняются условия теоремы Ролля, то внутри отрезка найдется по крайней мере одна такая точка, касательная в которой параллельна оси Ох.
Рис. 6.2
Теорема 3 (теорема Лагранжа). Если функция y f x
удовлетворяет двум условиям: 1) функция f(x) непрерывна на отрезке a;b ; 2) функция f(x) дифференцируема на интервале a;b ,
то внутри этого интервала найдется по крайней мере одна точка
x c , в которой производная f c f b f a . b a
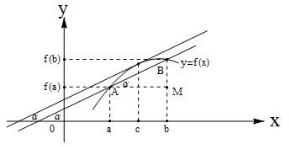
Геометрический смысл теоремы Лагранжа.
Если выполняются условия теоремы Лагранжа, то внутри отрезкаa;b найдется такая точка x c , касательная в которой параллельна
хорде, соединяющей концы дуги a; f a , b; f b .
Рис. 6.3
Теорема 4 (теорема Коши). Если функции y f x и y g x удовлетворяют условиям: 1) функции f(x) и g(x) непрерывны на отрезке a;b ; 2) функции f(x) и g(x) дифференцируемы на интервале
a;b , |
причем |
|
g x 0, x a;b , |
то внутри |
этого |
интервала |
||
найдется по |
крайней мере одна |
точка |
x c , |
в которой |
||||
|
f c |
f b f a |
|
|
|
|||
|
|
|
|
. |
|
|
(6.28) |
|
|
g c |
g b g a |
|
|
||||
Теорема Коши является обобщением теоремы Лагранжа.
В случае неопределенностей вида |
0 |
и |
|
при вычислении |
|
|
|
||||
0 |
|||||
|
|
|
пределов часто бывает полезным правило Лопиталя, которое задается следующей теоремой.
Теорема 1. Пусть функции f(x) и g(x) удовлетворяют
следующим условиям: |
|
|
||
1) |
определены и дифференцируемы в некоторой окрестности |
|||
точки |
x0 , |
за исключением, |
быть может, |
точки x0 , причем |
x O x0 g(x) 0 и g (x) 0, x x0 ; |
|
|||
2) |
lim f (x) lim g(x) 0 (либо lim f (x) lim g(x) ); |
|||
|
x x0 |
x x0 |
x x0 |
x x0 |
119
