Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

metodichkaFTUG_chast2

.pdf

Скачиваний:

Добавлен:

26.03.2016

Размер:

1.82 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 118 9 10 11 > Следующая >>>

3) существует конечный или бесконечный предел							lim	f (x)	,
3) существует конечный или бесконечный предел							lim	g (x)	,
							x x0	g (x)
тогда существует предел отношений функций lim					f (x)	,	причем
тогда существует предел отношений функций lim					g(x)	,	причем
				x x0	g(x)
lim	f (x)	lim	f (x)	.			(6.29)
lim		lim		.			(6.29)
x x0	g(x)	x x0	g (x)

Правило Лопиталя можно использовать последовательно несколько раз.

Аналогичное правило верно в случае x .

Если при вычислении пределов возникает неопределенность иного вида, то вначале пределы необходимо свести к

неопределенности вида

или

а затем

использовать

правило

Лопиталя.

В частности,

выражения 0 , тождественно преобразуют к

неопределенности вида

или

Неопределенности

вида 00 , 1 ,

возникают при

рассмотрении функции типа f (x) g ( x) . С помощью тождества

f (x) g( x) eg( x) ln f ( x)

(6.30)

они сводятся к неопределенности вида 0 , а затем – к

или

Если функция f(x) имеет в некоторой окрестности точки x x0

производные до ( n 1)-го порядка включительно, то при

x x0

верна формула Тейлора:

f (x) f (x

) f (x

)(x x

)

f (x0 )

(x x )2

...

(n) (x )

(6.31)

(x x )n R (x),

где Rn (x)

– остаточный член формулы Тейлора.

Существует

несколько

форм

записи

остаточного

члена.

В частности, в форме Лагранжа:

120

Rn (x) f (n 1) ( ) (x x0 )n 1 , (x0 , x). (n 1)!

Если в формуле Тейлора x0 0, получим частный вид формулы Тейлора – формулу Маклорена:

f (x) f (0)

f (0)

x2 ...

(n) (0)

xn R (x),

где Rn x - остаточный член в форме Лагранжа

Верны следующие формулы Маклорена:

...

R (x),

(6.32)

где

R (x)

xn 1

e x ,

0 1;

(n 1)!

sin x x

...

1 n 1

Rn (x),

(6.33)

xn 1

где

(x)

sin

x (n 1)

n N,

1)!

cos x 1

... 1 n

Rn (x),

(6.34)

xn 1

где

(x)

cos x (n 1)

n N,

1)!

ln(1 x) x

... ( 1)n 1

R (x),

(6.35)

где

R (x) ( 1)n 1

xn 1

, 0 1;

(n 1)(1 x)n 1

(1 x)m 1 mx

m(m 1)

...

m(m 1)...(m n 1)

xn R (x),

где

R (x)

m(m 1)...(m n)

(1 x)m n 1 xn 1,

0 1.

(n 1)!

Формулы Маклорена могут быть использованы в приближенных вычислениях. При этом абсолютная погрешность приближения в

121

случае чередования знаков в формуле Маклорена не превосходит абсолютной величины первого отбрасываемого слагаемого.

Пример 1. Вычислить предел функции с помощью правила Лопиталя:

e5x2

1) lim

;

lim

x 9

;

lim (2x )tg x;

x 1 4x

x x 2

x 2

lim

;

lim cos 2x x2 .

x 0 sin 3x

tg 3x

x 0

Решение. 1) Непосредственное вычисление предела дает

неопределенность вида

. Поскольку условия теоремы 1 выполняются,

используем правило Лопиталя. По формуле (6.29) имеем:

lim

5x2

lim

5x2

)

lim

5x2

)

lim

10xe

5x2

)

x 1 4x

x 1 (4x

x 1

(4x

x 1 12x

lim

10e5x2

10e5

e5 .

x 1

12x

2) Непосредственное вычисление предела дает неопределенность вида

, поэтому используем правило Лопиталя:

x 9

( x 9)

lim

2 x

2( 1)

x )

x x 2

x (x 2

2 x

lim

x 2

x (2

x 2)

x (2

x 2)

Имеем

неопределенность

вида

0 .

Поэтому, чтобы

воспользоваться правилом Лопиталя, преобразуем выражение, стоящее под знаком предела:

lim (2x )tg x (0 ) lim

lim

x 2

ctg x

tg x

lim

(2x )

lim

(ctg x)

x 2

sin2 x

4) Имеем неопределенность вида . Для того чтобы использовать

122

правило Лопиталя, преобразуем вначале выражение с помощью формул тригонометрии:

lim		2	1	(


x 0	sin 3x		tg 3x

) lim	2tg 3x sin 3x	0

x 0 sin 3x tg 3x		0

lim

x 0

		2 3		3cos 3x
(2tg 3x sin 3x)	lim	cos2	3x

(sin 3x tg 3x)					3sin 3x
	x 0 3cos 3x tg 3x
					cos2 3x

lim

6 3cos3

lim

6 3cos3 3x

x 0 3cos3 3x tg 3x

3sin 3x

0 3sin 3x cos2

3x 3sin 3x

3 lim

lim

x 0 3sin 3x cos2 3x 1

3 2 x 0 sin 3x

5) Так как приходим к неопределенности вида 1 , то вначале преобразуем выражение, стоящее под знаком предела:

1					lim	1	ln(cos 2 x)
lim cos 2x	x2		1	ex 0 x2				.
x 0
x 0				1						0 .
Получили		lim		1	ln(cos 2x),			неопределенность	вида
Получили		lim			ln(cos 2x),			неопределенность	вида
		x 0 x2

Преобразовав выражение, используем правило Лопиталя:

2 sin 2x

lim

ln(cos 2x)

lim

ln(cos 2x)

lim

cos 2x

x 0 x2

x 0

lim

tg 2x

x 0

Используем далее эквивалентность бесконечно малых:

lim	tg 2x	lim	2x	2.
	x		x
x 0		x 0
Пример 2. Разложить многочлен x5 3x4 x2 7x 1 по степени х + 2.

Решение. Используем формулу (6.31). В данном случае x0 2. Тогда

f ( 2) ( 2)5 3( 2)4 ( 2)2		7( 2) 1 89.
Найдем производные функции:
f (x) 5x4 12x3 2x 7;		f (4) (x) 120x 72;
f (x) 20x3	36x2 2;	f (5) (x) 120;
f (x) 60x2	72x;	f (6) (x) 0.

123

Все производные порядка выше пятого равны нулю. Вычислив значение полученных производных в точке х0 = –2, получаем:

f ( 2) 5 24 12 23 2 2 7 179;						f (4) (x) 120 2 72 312;
f ( 2) 20 23			36 22 2 302;			f (5) (x) 120.
f ( 2) 60 22 72 2 384;
Подставив найденные значения в формулу (6.31), получим:
x5 3x4 x			2 7x 1 89 179(x 2)				302	(x 2)2		384	(x 2)3

						2!			3!
	312	(x 2)4		120	(x 2)5 89 179(x 2) 151(x 2)2

4!			5!
64(x 2)3			13(x 2)4 (x 2)5.

Пример 3. Вычислить предел с помощью формул Маклорена:


1) lim	ex2		1	;	2) lim	1 cos3 x	.
		2x)				2x x2
x 0 ln(1					x 0

Решение. 1) Используем формулу Маклорена (6.32). Тогда

	x2		x2	x4		x2n	1
e		1 1			...		Rn	(x)	1.
e		1 1			...		Rn	(x)	1.
			1!	2!		n!
			1!	2!		n!

Выражение в правой части равенства эквивалентно величине x 0, так как остальные слагаемые имеют более высокий

малости («быстрее» стремятся к 0), т. е. ex2 1 ~ x2 . По формуле (6.35) получаем:

x2 при

порядок

ln(1 2x) 2x

(2x)2

(2x)3

... R2

(x) ~ 2x, если

x 0.

ex2

Тогда lim

lim

x 0 ln(1 2x)

x 0

Заметим, что более рациональное решение этого примера возможно с помощью таблицы эквивалентных бесконечно малых, так как использование формул Маклорена выступает здесь как способ доказательства эквивалентностей.

2) Преобразуя выражение под знаком предела и используя формулу (6.34), получим:

124

lim

1 cos3 x

lim

(1 cos x)(1 cos x cos2 x)

lim

1 cos x

0 2x x2

x 0

x(2 x)

2 x 0

... R (x)

lim

... Rn (x)

2 x 0

Пример 4. Используя формулу Маклорена, вычислить приближенное

значение ln1, 2

с точностью 0,001.

Решение. Используем формулу (6.35):

ln1, 2 ln(1

0, 2) ln 1

...

5 3

Поскольку

знаки

чередуются

0,0004 0,001,

то

достаточно

4 54

взять три слагаемых.

Получаем ln1, 2

0,183.

375

Задания для решения в аудитории

I уровень

1.1. Вычислите предел с помощью правила Лопиталя:

e x

3) lim

x2 x

;

1) lim

;

lim

2 2 cos x 2

x 0

sin x

x 0 x

x 0 arctg

ln x2 3

4) lim

x 8 2

;

lim

;

lim

a x

b x

x 0

x 0 x

2 3x 10

x 0

tg x

1.2. Используя формулу Тейлора, разложите многочлен P(x) по степеням (x a) :

1) P(x) x3 6x2 5x 2, a 1;

2)P(x) 2x3 7x2 13x 9, a 1;

3)y x4 3x3 2x2 x 1, a 2;

1.3.Используя известные формулы Маклорена, получите

формулу Маклорена для функции: 1) y sin2 x;

2) y ex2 .

125

IIуровень

2.1.Показать, что функция f(x) на отрезке a, b удовлетворяет условиям теоремы Ролля, и найти соответствующее значение с.

1) f (x) x x3 , 1; 0 .	2) f (x) 3		, 0; 8 .
		8x x2
2.2. На дуге параболы	y x2 , заключенной между точками

A 1; 1 и B 3; 9 . Найти точку, касательная в которой параллельная

хорде АВ.

2.3. Доказать неравенства, используя формулу Лагранжа:

arctg x

a-b

a b

, если 0 b a .

arctg x

a, b

2.4.

Показать,

что функция

f x e2 x

g x 1 e x на

удовлетворяют условиям теоремы Коши и найти соответствующее значение с.

2.5. Вычислите предел функции с помощью правила Лопиталя:

1)	lim	3sin2 x			1		;
1)	lim		ln cos x				;
	x 0		ln cos x
				1
4)	lim x2 e x2 .
	x 0
			1		ctgx
7)	lim							.
7)	lim							.
	x 0 x2					x

			1
2)	lim	e x2 1				.	3)	lim e 2x ln(6x 1);
2)	lim					.	3)	lim e 2x ln(6x 1);
	x 2arctg x2							x
	lim x tg			x				x		1
5)	lim x tg				.		6)	lim			.
	x			2				x 1 ln x
	x							x 1
		1								1	sin 3 x
8)	lim				ln 3x .			9)	lim			;
8)	lim				ln 3x .			9)	lim			;
	x 0 arctg x								x 0	x

	x 0	3		2	1
10)	lim 1 tg		x		sin	2 x	; . 11)

		x 5 x			cosx
lim	arcsin		;	12)	lim 2x

x 0		2			x
					2

2.6. Используя формулу Маклорена, вычислите приближенно с указанной точностью :

1) 329 ; 10 3 . 2) sin 360 ; 10 3 .

2.7. Разложите следующие функции по формуле Маклорена до члена указанного порядка включительно:

1) f (x) e x до члена с x3 ; 3) f (x) ln(sin x) до члена с x5 .

Задания для самостоятельного решения

126

1. Вычислить предел функции с помощью правила Лопиталя:

e3x 3x 1

ctg

lim

;

lim

;

lim

2x 1 1

;

x 0

sin 2 4x

x 2

x 1

x 2 x

lim

;

lim arctg 5x 2

;

lim arcsinx ctgx ;

x 0 x ln ex

x 0

lim

;

lim

tg x

;

lim cos 2x

;

cos x

x 0

x 2

10.

lim

x1 2ln x .

x 0

2. На дуге кривой

y x3

3x , заключенной между точками А(0; 0) и

В(3; 18), найти точку, касательная в которой параллельна хорде АВ.

3. Используя теорему Лагранжа для

функции y sin x

на x1, x2

x2 x1

доказать неравенство

sin x2 sin x1

Для

функций

f x x2

g x x3

проверить

выполнение

условий теоремы Коши на 1, 2 и найти соответствующее значение с.

5. Используя формулу Маклорена, вычислите приближенно с

указанной точностью :

10 3 .

cos100 ;

10 4 .

4 19 ;

6. Разложите x4 5x3

3x 4 по степеням (х - 4).

Написать

формулу

Маклорена

3-го порядка для функции

f (x) esin x .

Исследование функций с помощью производных.

6.6. Экстремумы функций. Интервалы монотонности функций. Наибольшее и наименьшее значение функций на

отрезке. Интервалы выпуклости и вогнутости. Точки перегиба

Всюду далее функция f(x) определена на рассматриваемых промежутках.

Теорема 1 (достаточное условие монотонности).

Дифференцируемая на (a, b) функция возрастает (убывает) на этом

127

интервале тогда и только тогда, когда f (x) 0 ( f (x) 0)

x (a,b).

Теорема 2 (необходимое условие существования экстремума функции). Если в точке x0 функция f(x) достигает экстремума, то ее

производная в этой точке равна нулю или не существует.

Те точки из области определения функции f(x), в которых производная функции f(x) обращается в нуль или не существует, называют критическими. Исследование функции на экстремум начинается с нахождения критических точек. Однако не в каждой критической точке существует экстремум. Для того чтобы определить точки экстремума, используют достаточные условия существования экстремума (признаки экстремума).

Теорема 3 (первый признак экстремума функции). Пусть x0 –

критическая точка непрерывной функции f(x). Если функция f(x) дифференцируема в некоторой окрестности точки x0 ,за

исключением быть может самой точки x0 , и при переходе через эту точку производная f x :

1)меняет знак с плюса на минус, то точка x0 - точка локального максимума;

2)меняет знак с минуса на плюс, то точка x0 - точка локального минимума;

3)не меняет знак, то x0 не является точкой экстремума.

Теорема 4 (второй признак экстремума функции). Пусть функция f(x) дважды дифференцируема в точке x0 и f x 0, а f x 0 . Тогда

x0 является	точкой локального минимума функции f(x), если
f (x0 ) 0, и точкой локального максимума, если f (x0 ) 0.
Теорема	5 (третий признак экстремума функции). Пусть f(x) – n

раз непрерывно дифференцируемая в критической точке x0 функция и

f	(x	) f (x ) ...	f (n 1) (x ) 0,			f (n) (x ) 0. Тогда:
	0	0		0					0
1)	если n – четное и		f (n) (x	) 0,	то	x	0		– точка локального максимума;
			0				0
2)	если n – четное и		f (n) (x	) 0,	то	x		0	– точка локального минимума;
			0					0
3)	если n – нечетное, то x0			не является точкой локального экстремума.

Замечание 1. При исследовании функции и построении ее графика

128

y (x);

целесообразно использовать первый признак экстремума, так как одновременно получаем возможность исследования функции на монотонность.

Точка x0 называется точкой глобального максимума

(минимума) функции f(x) на некотором промежутке, если для любой точки x из этого промежутка выполняется неравенство f (x) f (x0 )

f (x) f (x0 ) .

Точки глобального максимума и минимума называются

точками глобального экстремума. Значения функции в этих точках называются соответственно глобальным максимумом (наибольшим значением) и глобальным минимумом (наименьшим значением).

Теорема 6 (Вейерштрасса). Если функция f(x) непрерывна на отрезке, то она достигает на нем своих наименьшего и наибольшего значений.

Непрерывная на отрезке функция достигает наименьшего (наибольшего) значений либо на концах отрезка, либо в точках ее локального экстремума.

Для отыскания глобального экстремума функции f(x) на отрезке [a, b] необходимо: 1) найти производную 2) найти

критические точки функции; 3) найти значения функции на концах отрезка, т. е. f(a) и f(b), а также в критических точках, принадлежащих (a, b); 4) из всех полученных значений функции определить наибольшее и наименьшее ее значения.

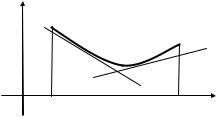
График	функции	y f (x) называется вогнутым	(выпуклым
вниз) на (a,	b), если	дуга кривой y f (x) на этом	интервале

расположена выше любой касательной, проведенной к графику этой функции (рис. 6.4).

		y f (x)
0	a	b	x

	Рис. 6.4
График функции	y f (x)	называется выпуклым (выпуклым

129

<<< < Предыдущая 1 2 3 4 5 6 78 / 118 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
31.05.20151.73 Mб20metodichka . физика.pdf
#
31.05.2015597.5 Кб16metodichka по МП пассажиров.doc
#
05.12.20189.82 Mб20Metodichka.doc
#
26.03.20161.61 Mб51MetodichkaC_14ch1.doc
#
26.03.20162.68 Mб20metodichkaFTUG_chast1.pdf
#
26.03.20161.82 Mб6metodichkaFTUG_chast2.pdf
#
10.11.20197.85 Mб10Metodichka_1_kurs.doc
#
26.03.201685.22 Кб12metodichka_magistranty.docx
#
31.05.20151.09 Mб4Metodichka_ME_i_VED.doc
#
20.12.2018310.78 Кб5metodichka_mido-progr.doc
#
11.09.2019825.86 Кб20Metodichka_po_diplomu.doc