Порядок выполнения работы

1. Положить груз на платформочку, прикрепленную к шнуру, найти суммарную массу mплатформочки и груза.

2. Вращая колесо, поднять груз на такую высоту, чтобы край платформочки совпадал с нулевым делением вертикальной шкалы.

3. Отпустив колесо, измерить время t, в течение которого груз опустится на высотуh.

4. Провести пять опытов, не изменяя массу груза и высоту падения.

Таблица измерений

m, г	d, мм	dси мм	t, с	tси, с	h, см	hси, см	g м/с2

5. С помощью штангенциркуля провести однократное измерение диаметра вала.

6. Результаты измерений и погрешности измерительных приборов занести в таблицу.

7. Произвести математическую обработку результатов измерений, найти момент инерции колеса Jи его погрешностьJ.

Контрольные вопросы

1. Виды движения твердого тела. Какое движение называется поступательным? вращательным?

2. Какие величины являются мерой инертности при поступательном и вращательном движении? Дайте их определение.

3. Сформулируйте теорему Штейнера.

4. Какие физические величины являются мерой воздействия при поступательном и вращательном движении?

5. Сформулируйте законы динамики поступательного и вращательного движения.

6. Ускорение при поступательном и вращательном движении. Угловое ускорение. Связь между линейными и угловыми кинематическими величинами.

7. Выведите расчетную формулу.

Лабораторная работа Определение момента инерции маятника Максвелла

Цель работы:изучение законов динамики поступательного и вращательного движения, экспериментальное определение момента инерции маятника Максвелла.

Приборы и принадлежности:маятник Максвелла, сменные кольца, электрический миллисекундомер, миллиметровая шкала.

Методика и техника эксперимента

Маятник Максвелла представляет собой массивный диск или колесо, к концам оси которого прикреплены два шнура; за концы этих шнуров маятник подвешивают к опоре.

Если шнуры намотать на ось и затем отпустить маятник, то под действием силы тяжести шнуры будут разматываться и маятник будет опускаться с ускорениема. Опустившись в крайнее нижнее положение, при котором шнуры полностью размотаны, колесо будет по инерции вращаться в том же направлении, шнуры намотаются на ось, вследствие чего маятник поднимется.

Применим законы динамики и кинематические уравнения для описания движения маятника Максвелла. Маятник участвует в двух движениях: прямолинейном движении центра масс с ускорением аи вращательном движении вокруг оси, проходящей через центр масс, с угловым ускорением. На маятник действуют сила тяжестиmgи сила натяжения нитиT.

С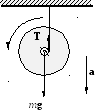огласно уравнению движения центра масс, совпадающему по форме с вторым законом Ньютона, имеем:

. (1)

Вращательное движение маятник совершает под действием момента силы натяжения нити T. Момент силы тяжести, приложенной к маховику, равен нулю, т.к. линия действия этой силы проходят через ось вращения. Применим основной закон динамики вращательного движения:

, (2)

где J- момент инерции маятника,- его угловое ускорение,- момент силыТ,- радиус вала,d- диаметр вала.

Ускорение маятника связано с угловым ускорением соотношением

. (3)

При равноускоренном движении

(4)

Разрешим систему уравнений (1) - (4) относительно момента инерции.

Из (3) выразим , из (1)и подставим в (2):

,

откуда момент инерции колеса определится выражением:

Учитывая, что согласно (4) , а, окончательно получим:

(5)

Установка, используемая в данной работе, состоит из вертикальной стойки, где крепятся два кронштейна: верхний 1 и нижний 2. Верхний кронштейн снабжен электромагнитом и устройством 3 для крепления бифилярного подвеса 4. Маятник представляет собой диск 5, закрепленный на оси 6, подвешенной на бифилярном подвесе.

Н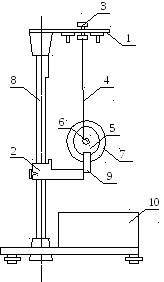а диск 5 крепятся сменные кольца 7. Маятник со сменными кольцами фиксируется в верхнем исходном положении с помощью электромагнита. На вертикальной стойке 8 нанесена миллиметровая шкала, имеющая пределы 0 - 420 мм. Фотодатчик 9 выдает электрические сигналы на миллисекундомер 10 с цифровой индикацией времени.