4. Гравитационное поле земли. Ускорение свободного падения Лабораторная работа 5-1 Определение ускорения свободного падения методом катающегося шарика

Цель работы:Определить ускорение свободного падения тел, изучая колебательное движение шарика на вогнутой поверхности.

Приборы и принадлежности: Вогнутая сферическая металлическая поверхность, шарик, секундомер, сферометр, штангенциркуль, миллиметровая линейка.

Методика и техника эксперимента

Установка для определения ускорения свободного падения представляет собой вогнутую сферическую чашу, по которой может свободно перемещаться шарик, совершая колебательное движение.

Если шар радиусаrпоместить на вогнутую поверхностьCABрадиуса, то он займет равновесное положение с минимальной потенциальной энергией, соприкасаясь с поверхностью в точкеА. При отклонении шара от положения равновесия (точкиВилиС) он придет в колебательное движение.

Пренебрегая трением, колебания с небольшой амплитудой можно считать незатухающими гармоническими.

Отклонение шарика от положения равновесия xбудем оценивать по положению центра инерции шарика (его геометрическому центру). При гармонических колебаниях зависимость смещения центра масс от времени имеет вид:

,

где а- амплитуда колебаний,Т- период. Найдем зависимость скорости центра масс от времени:

.

Шарик участвует в двух движениях: перемещении как целого со скоростью, равной скорости центра масс, и вращении относительно оси, проходящей через центр масс с угловой скоростью . При отсутствии проскальзывания

.

Скорости шарика, как линейная, так и угловая, принимают максимальное значение при прохождении шариком положения равновесия, когда :

, (1)

. (2)

Поскольку диссипативными процессами в системе можно пренебречь, применим закон сохранения механической энергии.

В крайних положениях шарик обладает потенциальной энергией

,

где - высота поднятия центра шарика над положением равновесия.

В положении равновесия шарик обладает кинетической энергией

.

где J – момент инерции шарика относительно его центра инерции.

Приравнивая эти выражения, получаем:

. (3)

Выразим высоту подъема Hчерез амплитудуa. Обозначим- радиус сферы, по которой движется центр шарика. Из геометрических соображений можно записать:

.

При малых амплитудах колебаний . Тогда,

. (4)

Момент инерции шарика относительно центра инерции равен

. (5)

Подставим в закон сохранения (3) энергии выражения (4), (1), (2), (5):

,

откуда после алгебраических преобразований получаем:

. (6)

Экспериментально с помощью сферометра измеряется радиус кривизны сферической вогнутой поверхности R^’=CO,поэтому

.

Если N -число полных колебаний шарика заtсекунд, то период колебаний равен

.

Тогда формула (6) примет вид

. (7)

Для определения радиуса сферической поверхности используется прибор, называемый сферометром. В его описании приведена формула вычисления радиуса сферической поверхности:

,

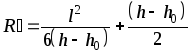где l- расстояния между ножками сферометра,h- отсчет по сферометру, помещенному на вогнутую поверхность,h₀- отсчет по сферометру, помещенному на плоскопараллельную пластинку.

При .

Выражение (7) приобретает вид расчетной формулы:

. (8)

где - диаметр шарика.